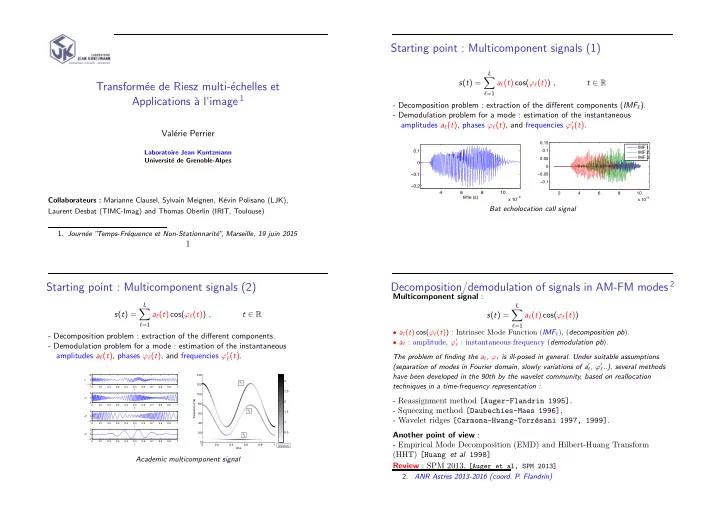

Starting point : Multicomponent signals (1) � L s ( t ) = a ℓ ( t ) cos( ϕ ℓ ( t )) , t ∈ R Transform´ ee de Riesz multi-´ echelles et ℓ =1 a l’image 1 Applications ` - Decomposition problem : extraction of the di ff erent components ( IMF ℓ ). - Demodulation problem for a mode : estimation of the instantaneous amplitudes a ℓ ( t ), phases ϕ ℓ ( t ), and frequencies ϕ ′ ℓ ( t ). Val´ erie Perrier 0.15 IMF 1 0.1 0.1 Laboratoire Jean Kuntzmann IMF 2 IMF 3 0.05 Universit´ e de Grenoble-Alpes 0 0 − 0.1 − 0.05 − 0.1 − 0.2 4 6 8 10 2 4 6 8 10 time (s) − 3 − 3 Collaborateurs : Marianne Clausel, Sylvain Meignen, K´ evin Polisano (LJK), x 10 x 10 Bat echolocation call signal Laurent Desbat (TIMC-Imag) and Thomas Oberlin (IRIT, Toulouse) 1. Journ´ ee ” Temps-Fr´ equence et Non-Stationnarit´ e” , Marseille, 19 juin 2015 1 Decomposition/demodulation of signals in AM-FM modes 2 Starting point : Multicomponent signals (2) Multicomponent signal : � L � L s ( t ) = a ℓ ( t ) cos( ϕ ℓ ( t )) , t ∈ R s ( t ) = a ℓ ( t ) cos( ϕ ℓ ( t )) ℓ =1 ℓ =1 • a ℓ ( t ) cos( ϕ ℓ ( t )) : Intrinsec Mode Function ( IMF ℓ ), ( decomposition pb ). - Decomposition problem : extraction of the di ff erent components. • a ℓ : amplitude, ϕ ′ ℓ : instantaneous frequency ( demodulation pb ). - Demodulation problem for a mode : estimation of the instantaneous amplitudes a ℓ ( t ), phases ϕ ℓ ( t ), and frequencies ϕ ′ ℓ ( t ). The problem of finding the a ℓ , ϕ ℓ is ill-posed in general. Under suitable assumptions (separation of modes in Fourier domain, slowly variations of a ′ ℓ , ϕ ′ ℓ ..), several methods have been developed in the 90th by the wavelet community, based on reallocation 10 140 0 s 3 s 1 techniques in a time-frequency representation : − 10 120 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 t 2.5 5 100 s 1 0 - Reassignment method [Auger-Flandrin 1995] , frequency (Hz) 2 − 5 80 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 t - Squeezing method [Daubechies-Maes 1996] , s 2 2 1.5 60 s 2 0 - Wavelet ridges [Carmona-Hwang-Torr´ esani 1997, 1999] . − 2 1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 40 t 2 20 0.5 Another point of view : s 3 s 3 0 − 2 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 - Empirical Mode Decomposition (EMD) and Hilbert-Huang Transform t 0 0.2 0.4 0.6 0.8 1 Amplitude time (HHT) [Huang et al 1998] Academic multicomponent signal Review : SPM 2013, [Auger et al, SPM 2013] 2. ANR Astres 2013-2016 (coord. P. Flandrin)
Motivation : Image decomposition/demodulation AM-FM Motivation : anisotropic texture analysis x ∈ R 2 f ( x ) = a ( x ) cos( ϕ ( x )) + f 1 ( x ) , - Decomposition problem : extraction of the di ff erent components. - Demodulation problem for a mode : estimation of the local amplitude a ( x ), phase ϕ ( x ), frequency ∇ ϕ ( x ). Texture with prescribed orientation Locally parallel textures [Polisano et al 2014] [Maurel-Aujol-Peyre 2011] Outline Outline Definitions Definitions 1 1 Hilbert transform and Analytic signal Hilbert transform and Analytic signal Riesz transform and Monogenic signal Riesz transform and Monogenic signal Computation of the Riesz Transform Computation of the Riesz Transform 2 2 via the Fourier domain via the Fourier domain via the Radon domain via the Radon domain In the direct space via a multiscale decomposition In the direct space via a multiscale decomposition Applications Applications 3 3 Local orientations from local Radon data Local orientations from local Radon data Decomposition/demodulation of Multicomponent Images Decomposition/demodulation of Multicomponent Images Conclusion Conclusion 4 4
Hilbert transform and Analytic signal Riesz transform and Monogenic Signal [Felsberg-Sommer 2001] � � R 1 f • 2D (or n-D) : Riesz Transform ⃗ Rf = R 2 f • 1D : Hilbert Transform . Let f : R → R H f in time domain : ⃗ Rf in space domain : � � � 1 � 1 � � � � � � 1 f ( s ) 1 ( x i − y i ) H f ( t ) = π vp ∗ f ( t ) = lim t − s ds for a.e. t ∈ R . R i f ( x ) = lim ∥ x − y ∥ 3 f ( y ) d y t π ε → 0 | t − s | > ε π ε → 0 + ∥ x − y ∥ > ε H f in Fourier domain : � | ξ | � f ( ξ ) = − i sgn( ξ ) � ξ H f ( ξ ) = − i f ( ξ ) Rf in Fourier domain : � ∥ ξ ∥ � ⃗ ξ i R i f ( ξ ) = − i f ( ξ ), for i = 1 , 2. � f � (ˆ • Analytic signal (complex) : F ( t ) = f ( t ) + i H f ( t ) F = 0 on R − ) • Monogenic (quaternionique) signal : M f = = f + i R 1 f + j R 2 f ⃗ Rf AM-FM analysis : F ( t ) = A ( t ) e i ϕ ( t ) AM-FM analysis : M f = A ( x ) e ϕ ( x ) n θ ( x ) - Instantaneous amplitude : A ( t ) = | F ( t ) | - Local amplitude : A ( x ) = |M f ( x ) | - Instantaneous frequency : ω ( t ) = ϕ ′ ( t ) - Local frequency : ω ( x ) = ∇ ϕ ( x ) - Local orientation : θ ( x ) ( n θ = cos θ i + sin θ j ) • Example : f ( t ) = A cos( ω t ). Then H ( f ) = A sin( ω t ) and F ( t ) = Ae i ω t (link with the orientation of ∇ ϕ ( x ) ?) − → A ( t ) = A , ϕ ( t ) = ω t Monogenic signal Outline 0 1 Definitions 1 „ f « cos( ϕ ( x )) Hilbert transform and Analytic signal = A ( x ) e ϕ ( x ) n θ ( x ) = A ( x ) @ A M f = sin( ϕ ( x )) cos( θ ( x )) ⃗ Rf Riesz transform and Monogenic signal sin( ϕ ( x )) sin( θ ( x )) • Example : f ( x ) = A 0 cos( k · x ). Let k = ( k 1 , k 2 ), θ 0 = Arctan ( k 2 k 1 ). Computation of the Riesz Transform 2 Then � sin( k · x ) cos θ 0 � via the Fourier domain k R f ( x ) = A 0 = A 0 | k | sin( k · x ) sin( k · x ) sin θ 0 via the Radon domain In the direct space via a multiscale decomposition and ⎛ ⎞ � f ( x ) � cos( k · x ) Applications 3 ⎝ ⎠ = A 0 e ( k · x )(cos θ 0 i +sin θ 0 j ) M f ( x ) = = A 0 sin( k · x ) cos θ 0 Local orientations from local Radon data R f ( x ) sin( k · x ) sin θ 0 Decomposition/demodulation of Multicomponent Images Finally Conclusion A ( x ) = A 0 , ϕ ( x ) = k · x , θ ( x ) = θ 0 = Arctan ( k 2 / k 1 ) . 4
Computation of the Riesz Transform (1) Computation of the Riesz Transform (2) • Via the Fourier domain : � | ξ | � R i f ( ξ ) = − i ξ i f ( ξ ), for i = 1 , 2. • Via the Radon domain [Felsberg 2002] Medical Scan : X-ray tomography Godfrey N. Hounsfield (ingenior in electronic) and Allan M. Cormack (mathematician) : Nobel Prize in Medicine 1979. Shepp and Logan phantom first component R 1 f second component R 2 f Fourier based Riesz computation : Involves a non local filtering (pb at frequency 0), Scan and illustration of its principle : X-ray taken around the patient. Requires the knowledge of the whole image , Computed using FFT , complexity : O ( N log 2 ( N )) Computation of the Riesz Transform (2) Computation of the Riesz Transform (2) • Inverse Radon transform : filtered back projection (FBP) • Radon Transform : � π �� + ∞ � f ( x ) = R − 1 ( R f ( θ , s )) = R θ f ( ω ) | ω | e 2 i πω ( x . ⃗ � θ ) d ω d θ 0 −∞ (where d R θ f denotes the 1D Fourier transform of R θ f . Remark : involves the non local ramp filter | ω | . • Original Radon-based Riesz formula [Felsberg 2002], [Soulard-Carr´ e 2012] Rf ( x ) = R − 1 �� � � ⃗ ⃗ HR ⃗ θ f θ ( x ) The Radon transform of function f ( x ) is measured on each detector of direction ⃗ θ = (cos θ , sin θ ) , corresponding to the mean of f along lines L θ , s of direction due to : θ ⊥ = ( − sin θ , cos θ ) : ⃗ � π �� + ∞ � � � � � + ∞ | ω | e 2 i πω ( x · ⃗ ⃗ � ⃗ θ ) d ω Rf ( x ) = R θ f ( ω )( − i )sign( ω ) θ d θ f ( s ⃗ θ + t ⃗ θ ⊥ ) dt R f ( θ , s ) = R θ f ( s ) = f ( x ) d ℓ = 0 −∞ L θ , s −∞ Remark : involves two non local operators : the Hilbert transform H and the inverse Radon transform R − 1 .
Computation of the Riesz Transform (2) Computation of the Riesz Transform (2) • Interest : local Riesz transform from local Radon data • Local Radon-based Riesz formula [Desbat-P 2015] Since : �� + ∞ � � π R θ f ( ω )( − i ω ) e 2 i πω ( x · ⃗ � ⃗ θ ) d ω ⃗ Rf ( x ) = θ d θ 0 −∞ Then : � π � � Rf ( x ) = − 1 ∂ R f ⃗ θ , x · ⃗ ⃗ θ θ d θ 2 π ∂ s 0 Phantom and ROI Radon data Truncated Radon data Local ( R 1 f , R 2 f ) with NO ERROR Non local Radon based Riesz Local Radon based Riesz Computation of the Riesz Transform - In direct space (3) Computation of the Riesz Transform - In direct space (4) Monogenic Wavelet Transform - [Olhede-Metikas 2009], [Unser-VanDeVille 2009] • Pyramidale decomposition [Burt-Adelson 1983] • 2D directional CWT � � � ψ a , b , α ( x ) = 1 x − b c f ( a , b , α ) = R 2 f ( x ) ψ a , b , α ( x ) d x , a ψ r − α a If ψ is isotropic, ψ a , b , α = ψ a , b , 0 = ψ a , b . Denote c f ( a , b ) = c f ( a , b , 0). • Isotropic CWT of the monogenic signal F = M f = f + R 1 f i + R 2 f j | k a | � • Multiscale Riesz transform : in each band a , � ξ i R i f a ( ξ ) = − i f a ( ξ ) c F ( a , b ) = ( c f + c R 1 f i + c R 2 f j ) ( a , b ) − 1 ∂ f a → R i f ∼ 2 π k a ∂ x i • Monogenic Wavelet Transform ( ψ real isotropic) � c ( M ) ( a , b , α ) = R 2 f ( x ) ( M ψ ) a , b , α ( x ) d x f � � 1 0 c ( M ) c F ( a , b ) = ( a , b , α ) 0 − r α f → Complexity : linear ! [Wahdwa-Rubinstein-Durand-Freeman 2014] for video � Ae ( k · b ) n θ � • Example : F ( x ) = A e ( k · x ) n θ , c F ( a , b ) = a � ψ ( ak ) magnification
Recommend
More recommend