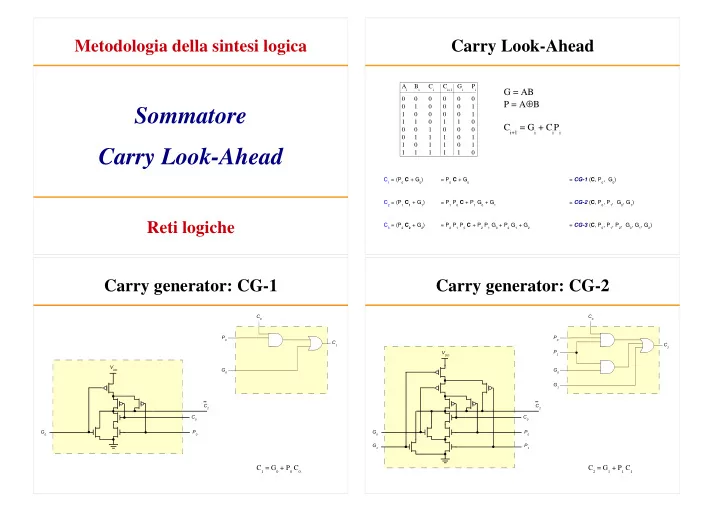

Metodologia della sintesi logica Carry Look-Ahead A i B i C i C i+1 G i P i G = AB 0 0 0 0 0 0 P = A ⊕ B 0 1 0 0 0 1 Sommatore 1 0 0 0 0 1 1 1 0 1 1 0 C i+1 = G i + C i P i 0 0 1 0 0 0 0 1 1 1 0 1 1 0 1 1 0 1 Carry Look-Ahead 1 1 1 1 1 0 C 1 = (P 0 C + G 0 ) = P 0 C + G 0 = CG-1 ( C , P 0 , G 0 ) C 2 = (P 1 C 1 + G 1 ) = P 1 P 0 C + P 1 G 0 + G 1 = CG-2 ( C , P 0 , P 1 , G 0 , G 1 ) Reti logiche C 3 = (P 2 C 2 + G 2 ) = P 2 P 1 P 0 C + P 2 P 1 G 0 + P 2 G 1 + G 2 = CG-3 ( C , P 0 , P 1 , P 2 , G 0 , G 1 , G 2 ) Carry generator: CG-1 Carry generator: CG-2 C 0 C 0 P 0 P 0 C 1 C 2 P 1 V DD V DD G 0 G 0 G 1 C 2 C 2 C 0 C 0 G 0 P 0 G 0 P 0 G 1 P 1 C 1 = G 0 + P 0 C 0 C 2 = G 1 + P 1 C 1
Carry generator: CG-3 Carry Look-Ahead: 4-bit A 0 ,A 1 ,A 2 ,A 3 B 0 ,B 1 ,B 2 ,B 3 C 0 4 4 Setup V DD P 0 4 4 C 3 P 1 P 0 ,P 1 ,P 2 ,P 3 G 0 ,G 1 ,G 2 ,G 3 P 2 P 0 G 0 P 0 ,P 1 G 0 ,G 1 P 0 ,P 1 ,P 2 G 0 ,G 1 ,G 2 G 0 2 2 3 3 CG-1 G 1 CG-2 C 3 CG-3 G 2 C 0 C 0 G 0 P 0 A 0 B 0 A 1 B 1 A 2 B 2 A 3 B 3 C 1 C 2 C 3 G 1 P 1 G 2 P 2 SUM SUM SUM SUM C 3 = G 2 + P 2 C 2 S 0 S 1 S 2 S 3 Carry Look-Ahead: 4-bit Carry Look-Ahead: 16-bit A 0 ,A 1 ,A 2 ,A 3 B 0 ,B 1 ,B 2 ,B 3 C 4 = (P 3 C 3 + G 3 ) = P 3 P 2 P 1 P 0 C + P 3 P 2 P 1 G 0 + P 3 P 2 G 1 + P 3 G 2 + G 3 = P [0,3] C + G [0,3] 4 4 Setup 4 4 P [0,3] = P 3 P 2 P 1 P 0 P 0 ,P 1 ,P 2 ,P 3 G 0 ,G 1 ,G 2 ,G 3 G [0,3] = P 3 P 2 P 1 G 0 + P 3 P 2 G 1 + P 3 G 2 + G 3 = CG-3 ( G 0 , P 1 , P 2 , P 3 , G 1 , G 2 , G 3 ) P 0 G 0 P 0 ,P 1 G 0 ,G 1 P 0 ,P 1 ,P 2 G 0 ,G 1 ,G 2 2 2 3 3 C 4 = CG-1 ( C , P [0,3] , G [0,3] ) Carry Generator C 5 = (P 4 C 4 + G 4 ) = CG-1 ( C 4 , P 4 , G 4 ) C 0 A 0 B 0 A 1 B 1 A 2 B 2 A 3 B 3 C 1 C 2 C 3 C 6 = (P 5 C 5 + G 5 ) = P 5 P 4 C 4 + P 5 G 4 + G 5 = CG-2 ( C 4 , P 4 , P 5 , G 4 , G 5 ) SUM SUM SUM SUM C 7 = (P 6 C 6 + G 6 ) = P 6 P 5 P 4 C 4 + P 6 P 5 G 4 + P 6 G 5 + G 6 = CG-3 ( C 4 , P 4 , P 5 , P 6 , G 4 , G 5 , G 6 ) S 0 S 1 S 2 S 3
Carry Look-Ahead: 16-bit Carry Look-Ahead: 16-bit C 8 = (P 7 C 7 + G 7 ) = P 7 P 6 P 5 P 4 C 4 + P 7 P 6 P 5 G 4 + P 7 P 6 G 5 + P 7 G 6 + G 7 = C 12 = (P 11 C 11 + G 11 ) = P 11 P 10 P 9 P 8 P [4,7] P [0,3] C + P 11 P 10 P 9 P 8 P [4,7] G [0,3] + = P 7 P 6 P 5 P 4 P [0,3] C + P 7 P 6 P 5 P 4 G [0,3] + P 7 P 6 P 5 G 4 + P 7 P 6 G 5 + P 7 G 6 + G 7 = = P [4,7] P [0,3] C + P [4,7] G [0,3] + G [4,7] P 11 P 10 P 9 P 8 G [4,7] + P 11 P 10 P 9 G 8 + P [4,7] = P 7 P 6 P 5 P 4 P 11 P 10 G 9 + P 11 G 10 + G 11 = G [4,7] = P 7 P 6 P 5 G 4 + P 6 G 5 + P 7 G 6 + G 7 = CG-3 ( G 4 , P 5 , P 6 , P 7 , G 5 , G 6 , G 7 ) = P [8,11] P [4,7] P [0,3] C + P [8,11] P [4,7] G [0,3] + P [8,11] G [4,7] + G [8,11] C 8 = CG-2 ( C , P [0,3] , P [4,7] , G [0,3] , G [4,7] ) P [8,11] = P 11 P 10 P 9 P 8 G [8,11] = P 11 P 10 P 9 G 8 + P 11 P 10 G 9 + P 11 G 10 + G 11 = CG-3 ( G 8 , P 9 , P 10 , P 11 , G 9 , G 10 , G 11 ) C 9 = CG-1 ( C 8 , P 8 , G 9 ) C 13 = CG-1 ( C 12 , P 12 , G 12 ) C 10 = CG-2 ( C 8 , P 8 , P 9 , G 8 , G 9 ) C 14 = CG-2 ( C 12 , P 12 , P 13 , G 12 , G 13 ) C 11 = CG-3 ( C 8 , P 8 , P 9 , P 10 , G 8 , G 9 , G 10 ) C 15 = CG-3 ( C 12 , P 12 , P 13 , P 14 , G 12 , G 13 , G 14 ) Carry Look-Ahead: 16-bit Carry Look-Ahead: 64-bit C 16 = CG-1 ( C , P [0,15] , G [0,15] ) P i = A i � B i G i = A i · B i Setup (P , G) P [0,15] = P [12,15] P [8,11] P [4,7] P [0,3] Setup P [12,15] = ... G [12,15] = ... G [0,15] = P [12,15] P [8,11] P [4,7] G [0,3] + P [12,15] P [8,11] G [4,7] + P [12,15] G [8,11] + G [12,15] = P [0,3] = P 3 P 2 P 1 P 0 P [4,7] = P 7 P 6 P 5 P 4 P [8,11] = P 11 P 10 P 9 P 8 = CG-3 ( G [0,3] , P [4,7] , P [8,11] , P [12,15] , G [4,7] , G [8,11] , G [12,15] ) G [0,3] = CG-3 ( G 0 , P 1 , P 2 , P 3 , G 1 , G 2 , G 3 ) G [4,7] = CG-3 ( G 4 , P 5 , P 6 , P 7 , G 5 , G 6 , G 7 ) G [8,11] = CG-3 ( G 8 , P 9 , P 10 , P 11 , G 9 , G 10 , G 11 ) G [0,3] P [0,3] G [4,7] P [4,7] G [8,11] P [8,11] C 32 = CG-2 ( C , P [0,15] , P [16,31] , G [0,15] , G [16,31] ) C 0 Carry Generator P [16,31] = P [28,31] P [24,27] P [20,23] P [16,19] C 4 C 8 C 12 G [16,31] = CG-3 ( G [16,19] , P [20,23] , P [24,27] , P [28,31] , G [20,23] , G [24,27] , G [28,31] ) G 0 P 0 G 1 P 1 G 2 P 2 G 4 P 4 G 5 P 5 G 6 P 6 G 8 P 8 G 9 P 9 G 10 P 10 G 12 P 12 G 13 P 13 G 14 P 14 C 48 = CG-3 ( C , P [0,15] , P [16,31] , P [31,47] , G [0,15] , G [16,31] , G [31,47] ) C 0 Carry Generator Carry Generator Carry Generator Carry Generator P [32,47] = P [44,47] P [40,43] P [36,39] P [32,35] C 5 C 6 C 7 C 9 C 10 C 11 C 13 C 14 C 15 C 1 C 2 C 3 G [32,47] = CG-3 ( G [32,35] , P [36,39] , P [40,43] , P [44,47] , G [36,39] , G [40,43] , G [44,47] ) SUM
Carry Look-Ahead: 64-bit Carry Look-Ahead: delay P i = A i � B i G i = A i · B i Setup (P , G) � P[...] and G[...] signals Setup – do not depend on C 0 P [0,15] = P [12,15] P [8,11] P [4,7] P [0,3] P [16,31] = ... P [32,47] = ... P [48,63] = ... – propagate from lower levels to higher levels of hierarchy G [0,15] = CL-3 ( G [0,3] , P [4,7] , P [8,11] , P [12,15] , G [4,7] , G [8,11] , G [12,15] ) G [16,31] = ... G [32,47] = ... G [48,63] = ... � C i signals 8 G [0,15] P [0,15] G [16,31] P [16,31] G [32,47] P [32,47] C 0 Carry Generator – propagate from higher levels of hierarchy to final adders G [0,3] , G [4,7] , G [8,11] , G [12,15] P [0,3] , P [4,7] , P [8,11] , P [12,15] Setup Setup Setup Setup C 0 Carry generators (2 levels) Carry generators (2 levels) Carry generators (2 levels) Carry generators (2 levels) SUM Carry Look-Ahead: delay Carry Look-Ahead: delay � T s = delay of Setup P, G � Latency for generation of G[] = (L-1) · T G3 � L = hierarchy levels � Latency for generation of last C = L · T G3 – L = log 4 n � T sum = delay of A i � B i � C i � T CLA (n) = T s + (L-1) · T G3 + L · T G3 + T sum � T G3 = delay of CG-3 � T CLA (n) � log 4 n – standard cells: T G ~ 2 · T G – standard cells: T CLA (n) ~ T G + (L-1)·2·T G + L·2·T G + T G T CLA (n) ~ (1 + 4 · log 4 n) · T G
Recommend
More recommend