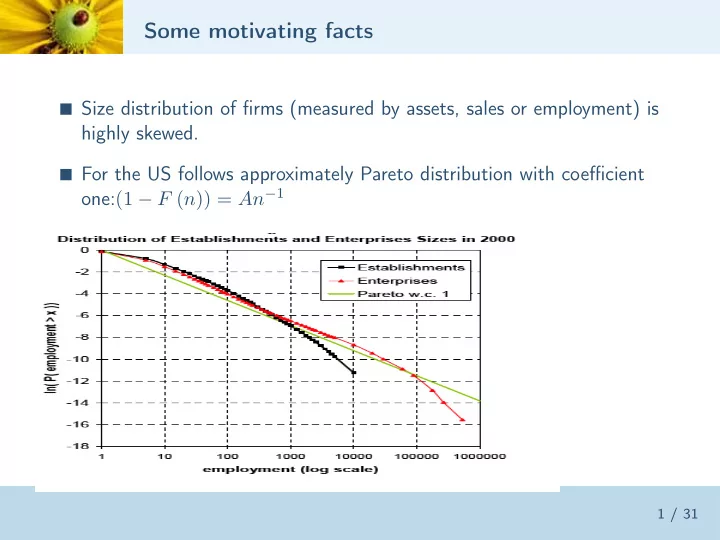
Some motivating facts Size distribution of firms (measured by - PowerPoint PPT Presentation

Some motivating facts � Size distribution of firms (measured by assets, sales or employment) is highly skewed. � For the US follows approximately Pareto distribution with coefficient one: (1 − F ( n )) = An − 1 1 / 31

more facts � Firm size is persistent but the variance of innovations is quite large. � Gross realocation of employment across firms exceeds in several orders of magnitude net reallocation. � Variance of growth rates declines with size and age. � Firm size increases with age. � There is considerable degree of entry/exit into narrowly defined industries. Small and young firms have higher exit rates. � Most firm level changes in employment correspond to idiosyncratic shocks, i.e. not explained by aggregate, geographic or industry variables. 2 / 31

A simplified Lucas model � Collection of firms i = 1 , ..., M � Technology y i = e i n η i where η < 1 � Fixed endowment of labor N � Competitive equilibrium { w, n i } maximizing profits and market clearing. � n ( e i , w ) labor demand and � n ( e i , w ) = N � Solves planner problem: i e i n η � max n i i � i n i ≤ N 3 / 31

Equilibrium � Employment: 1 1 − η n i = ae i 1 � 1 − η a e = N i η 1 a η e i e = a η e 1 − η 1 − η y i = i i � Remark y i /n i is the same for all fi rms! � Solving for w and substituting: 1 � y i = a η � 1 − η y = e i i � 1 − η �� 1 N η 1 − η = e i 4 / 31

The Aggregate Production function � 1 − η �� 1 N η 1 − η y = e i � 1 − η � 1 M 1 − η N η 1 − η = E i e i � Cobb Douglass in M, N with TFP equal to geometric average of firm shocks. � M is like a capital stock, sometimes called "organization capital" � Intangible? 5 / 31

Multiple inputs � Results generalize to multiple inputs (Lucas 1978) � Let f ( x ) be homogenous of degree one and y i = e i ( f ( x )) η � aggregate endowment vector X � Aggregate production function: � 1 − η � 1 M 1 − η f ( X ) η 1 − η y = E i e i 6 / 31

Large number of firms � Let F ( e ) denote the cdf for shocks. � Suppose M is the mass of firms (quantity of organization capital) � 1 − η � 1 M 1 − η N η y = Ee 1 − η � α Pareto distribution � e min � Special case: F = 1 − e αe min 1 1 − β − α 1 1 − η = Ee e min 1 α − 1 − η 1 � "Tail condition": defined only when α > 1 − η 7 / 31

Endogenizing entry � Technology for creating firms (organization capital) takes c e workers. � Entrants draw e i independently from same distribution � Planner’s problem: � 1 − η � 1 M 1 − η L η max M,L Ee 1 − η subject to : c e M + L ≤ N � solution: L = ηN and M = (1 − η ) N/c e  � 1 − η  1 � Ee 1 − η (1 − η ) 1 − η η η  N y =  c e � Constant returns to scale in aggregate 8 / 31 � Productivity negatively related to entry cost.

Connection to monopolistic competition � Dixit-Stiglitz (1977), Melitz (2003) � 1 y η � ´ � Continuum of goods: y = i di η � Linear techology y i = e η i n i η ( w/e η � Constant markup p i = 1 i ) 1 � y η 1 − η i ∝ e and so is n i i � 1 − η � 1 η 1 − η η N 1 − η y = Ee M i � 1 − η � 1 y η M 1 − η N η 1 − η = Ee i � With endogenous entry get same M. 9 / 31

General or partial equilibrium � Partial equilibrium: � Aggregate demand D ( p ∗ ) � Cost function c ( e, q ) , supply function s ( e, p ) � Entry cost c e � Solve for unique p ∗ that makes expected profits = c e � Find ME e s ( e, p ∗ ) = D ( p ∗ ) � Correspondence ( w = 1) , � c ( e, q ) = f − 1 ( q/e ) � p ∗ = 1 /w ∗ 10 / 31

Firm dynamics - motivation � Lots of evidence that firms’ size is not constant � Five year AR1 of firm ln employment US manufacturing, persistence 0.92 and large variance of innovation. � Firm size distribution stochastically increases with age. � average entrant 35% size of average incumbent 11 / 31

Firm dynamics - simple model � entrants draw independently initial shocks from same distribution � firm productivity evolves according to MP F ( e t +1 | e t ) � Repeated application generates probability distributions ˜ µ s for firms of age s. � exogenous death/exit rate 1 − δ . δ t m 0 + δ t − 1 m 1 + ... + δm t − 1 + m t M t = µ 1 + ... + δ t m 0 ˜ � � µ t = M − 1 m t ˜ µ 0 + δm t − 1 ˜ µ t t � 1 − η � ˆ 1 M 1 − η L η 1 − η dµ t ( e ) y t = e t t 12 / 31

Competitive equilibrium Given sequence of wages w = { w t } ∞ t =0 max n en η − w t n + βδEv t +1 � � e � ; w | e v t ( e ; w ) = v e = E 0 v t ( e ; w ) − w t c e t Definition 1. A competitive equilibrium is a sequence { m t , n t ( e ) , v t } and wages { w t } that satisfy the following conditions: 1. Employment decisions are optimal given wages 2. value functions are as defined above 3. v e t ≤ 0 and m t v e t = 0 ´ 4. m t c e + n t ( e ) µ t ( de ) = N . 13 / 31

Planners problem � Objective: � 1 − η 1 t =0 β t � ´ M 1 − η L η 1 − η dµ t ( e ) � ∞ max m t ,L t e t t M t = δ t m 0 + δ t − 1 m 1 + ... + m t subject to : L + c e m t = N � Unique solution: � Objective strictly concave � Constraints linear 14 / 31

Stationary equilibrium � Analogous to steady state (or balanced growth path) � Entry flow m t = m for all t. m s =0 δ s ˜ 1 − δ and µ = (1 − δ ) � ∞ � This implies M = µ s � Value function: ˆ v ( e ) = max n en η − wn + βδ � e � � � de � e � v F ´ � Resource constraint: n ( e, w ) dµ ( e ) + mc e = N � Stationary equilibrium is unique. � 1 − η � 1 1 − η Ee � Steady state productivity proportional to: c e 15 / 31

Costs of entry and TFP � Cross-country regression (Moscoso-Boedo and Mukoyama, 2010) � Calculate regulatory costs of creating business measured in units of annual labor κ � Lowest US κ = 0 . 3 , highest Liberia κ = 616 . 8 , 29 countries with κ < 1 and 31 with κ > 10 . Entry Cost 6 5 4 3 log( � ) 2 1 0 � 1 � 2 � 7 � 6 � 5 � 4 � 3 � 2 � 1 0 1 Log (GNI p cap relative to US) 16 / 31

Effects of entry costs in the model � From our previous derivations: � 1 − η   1 � Ee 1 − η (1 − η ) 1 − η η η  N y =  c e + κ d ln y/d ln ( c + κ ) = − (1 − η ) � E ff ects of distortions to entry costs depend on the degree of decreasing returns � usually take η = 0 . 85 , so d ln y/d ln κ = − 0 . 15 � Back of the envelope (Moscoso-Boedo and Mukoyama) � baseline c e = 36 . Compare κ = 10 and κ = 100 to κ = 0 � κ = 10 → TFP = 0 . 9 , κ = 100 → TFP = 0 . 6 17 / 31 � Sizeable but far from observed di ff erences in TFP.

Firm dynamics � Stylized facts: � Small firms grow faster (conditional on survival) � Size of firms very persistent (close to random walk) � Large firms have lower variance of growth rates � Size distribution of firms stochastically increasing in age � Exit rates decline with age � Last one cannot be explained in this model that assumes a constant exit rate � Others depend on assumptions on the distribution F and the initial distribution of firms shocks, call it G. 18 / 31

Age-increasing size distribution Assumption 1. (FOSD) F ( e � , e ) decreasing in e. ´ µ s +1 ([0 , e � ]) = F ([0 , e � ] , e ) d ˜ � Sequence ˜ µ s obtained recursively as ˜ µ s ( e ) ´ F ([0 , e � ] , e ) dG ( e ) < G ([0 , e � ]) Assumption 2. F ◦ G � G (F increases G ): � Persistence and F ◦ G � G implies ˜ µ s is increasing sequence (in FOSD) 19 / 31

Endogenous exit and selection � Firm exit endogenous � Need a reason for exiting: fixed costs, opportunity costs � Assume fixed cost f denominated in units of labor � �� ˆ � e � ; w � � de � , e v ( e ; w ) = max 0 , π ( e, w ) + β v F � Decision rules n ( e, w ) and exit set E ( w ) . Proposition 1. ( i ) v ( e ; w ) strictly decreasing in w if nonzero. ( ii ) Under (FOSD) v ( e ; w ) strictly increasing in e if nonzero and exit set is threshold e ( w ) . � Value of entry: v e ( w ) = ´ v ( e ; w ) dG ( e ) − c e 20 / 31

The invariant measure of firms � Timing: 1) entry; 2) shocks realized, 3) exit; 4) production � Entrants: m mass: measure mG ´ � Incumbents (before exit): µ I ( −∞ , e ) = F ( e, e 0 ) µ ( de 0 ) � New measure of firms ( e ≥ e ∗ ) Tµ ( −∞ , e ) = m [ G ( e ) − G ( e ∗ )] + µ I ( e ∗ , e ) ˆ = m [ G ( e ) − G ( e ∗ )] + [ F ( e, e 0 ) − F ( e ∗ , e 0 )] µ ( de 0 ) � Invariant measure: µ = Tµ 21 / 31

Unique invariant measure � Invariant measure as a weighted sum of measure of di ff erent cohorts. � Let α n be the probability of surviving up to n periods ∞ � µ = m α n ˜ µ n n =0 � Necessary and Su ffi cient conditoin for existence : ∞ � α n < ∞ n =0 � Integrating by parts: finite expected lifetime ∞ ∞ � � α n = n ( α n +1 − α n ) < ∞ n =0 n =0 22 / 31

Stationary equilibrium: definition { µ, e ∗ , m, w } 1. v e ( w ) ≤ 0 and v e ( w ) m = 0 2. e ∗ is optimal exit rule ´ 3. N = ( f + n ( e, w )) dµ + mc e 4. µ is an invariant measure � Equilibrium with entry and exit � m > 0 ´ � m (1 − G ( e ∗ )) = F ( e ∗ , e ) µ ( ds ) � v e ( w ∗ ) = 0 � unique 23 / 31