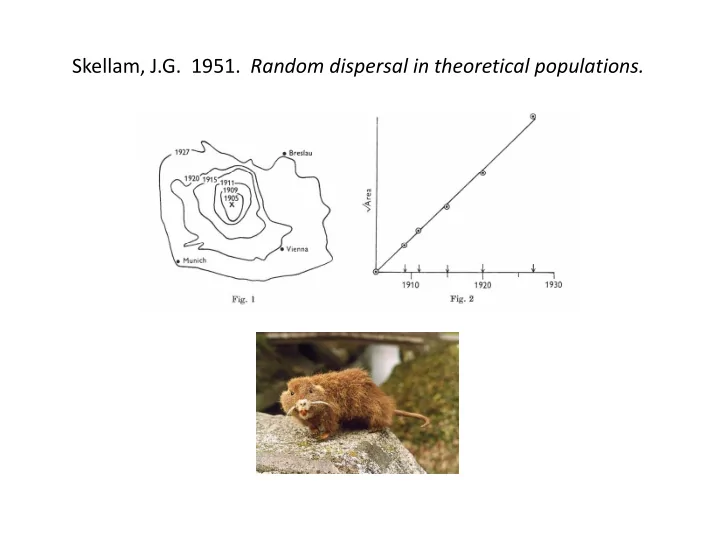
Skellam, J.G. 1951. Random dispersal in theoretical populations. E.E. - PowerPoint PPT Presentation

Skellam, J.G. 1951. Random dispersal in theoretical populations.

E.E. Holmes, 1993. Are diffusion models too simple? A comparison with telegraph models of invasion p g p f Motivation: Diffusion models possess weird (non ‐ biological) microscopic properties. (Ex: infintesimally small chance of infinitely fast movement.) Telegraph dispersal:  : constant velocity  : stochastic turning rate  : stochastic turning rate

E.E. Holmes, 1993. Are diffusion models too simple? A comparison with telegraph models of invasion p g p f Invasion speeds predicted by reaction ‐ diffusion models vs. reaction ‐ telegraph models: c 1   tele    r c c    1 1   diff diff    2

Stochastic dynamics of invasive Stochastic dynamics of invasive y spread spread Brett Melbourne & Alan Hastings U i University of California, Davis i f C lif i D i

Flour beetle: castaneum Tribolium 4 cm Experiment Experiment

4 cm Tunnel Hole Experiment Experiment

Lifecycle in laboratory Lifecycle in laboratory  Discrete time (35 day cycle) 1) Adults lay eggs (24 hr) 1) Adults lay eggs (24 hr)  Fences installed; adults removed 2) Larvae grow 2) Larvae grow  Adults emerge (ca day 30) 3) Adults disperse (48 hr)  Census after dispersal

Experiment Experiment  30 landscapes  Constant  Constant environment  13 generations  13 generations