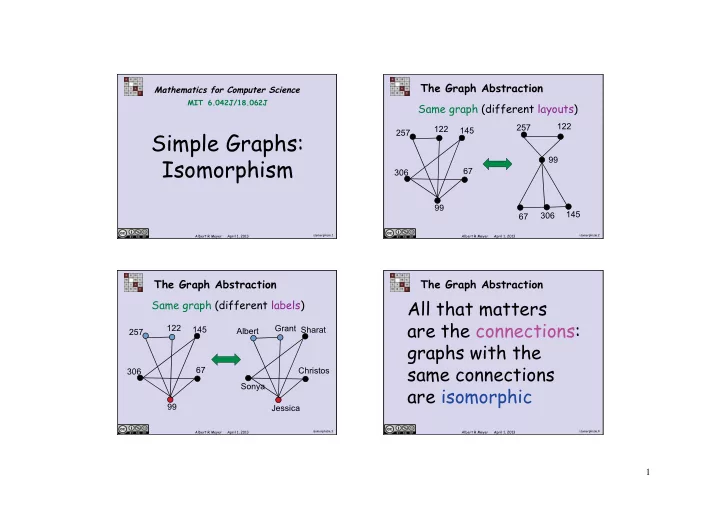
simple graphs
play

Simple Graphs: 99 Isomorphism 67 306 99 145 306 67 - PowerPoint PPT Presentation

Oct 08, 2023 •267 likes •328 views

The Graph Abstraction Mathematics for Computer Science MIT 6.042J/18.062J Same graph (different layouts) 122 257 122 145 257 Simple Graphs: 99 Isomorphism 67 306 99 145 306 67 isomorphism.1 isomorphism.2 Albert R Meyer April 1,

  1. The Graph Abstraction Mathematics for Computer Science MIT 6.042J/18.062J Same graph (different layouts) 122 257 122 145 257 Simple Graphs: 99 Isomorphism 67 306 99 145 306 67 isomorphism.1 isomorphism.2 Albert R Meyer April 1, 2013 Albert R Meyer April 1, 2013 The Graph Abstraction The Graph Abstraction Same graph (different labels) All that matters are the connections: 122 Grant 145 Sharat Albert 257 graphs with the 67 same connections Christos 306 Sonya are isomorphic 99 Jessica isomorphism.3 isomorphism.4 Albert R Meyer April 1, 2013 Albert R Meyer April 1, 2013 1

  2. Isomorphism Are these isomorphic? two graphs are isomorphic Hay when there is an Dog Pig edge-preserving Corn matching Cow Cat Beef Tuna of their vertices. f(Dog) = Beef f(Cow) = Hay f(Cat) = Tuna f(Pig) = Corn isomorphism.5 isomorphism.6 Albert R Meyer April 1, 2013 Albert R Meyer April 1, 2013 Edges preserved? Edges preserved? YES! Hay Hay Dog Dog Pig Pig Corn Corn Cow Cow Cat Cat Beef Beef Tuna Tuna isomorphism.7 isomorphism.8 Albert R Meyer April 1, 2013 Albert R Meyer April 1, 2013 2

  3. YES! Nonedges preserved? Formal Def of Graph Isomorphism G 1 isomorphic to G 2 means Hay edge-preserving vertex matching : Dog Pig ∃ bijection f:V 1 � V 2 with Corn u—v in E 1 IFF f(u)—f(v) in E 2 Cow Cat Beef Tuna isomorphic! isomorphism.9 isomorphism.10 Albert R Meyer April 1, 2013 Albert R Meyer April 1, 2013 Nonisomorphism Proving nonisomorphism If some property preserved by isomorphism differs for two graphs, then they’re not isomorphic: # of nodes, # of edges, degree distributions, … . degree 2 all degree 3 isomorphism.11 isomorphism.12 Albert R Meyer April 1, 2013 Albert R Meyer April 1, 2013 3

  4. Are these two graphs isomorphic? Finding an isomorphism? many possible mappings: large search can use properties preserved by isomorphisms as a guide, for example: • a deg 4 vertex adjacent to a deg 3 can only match with ...nothing known is sure to be • a deg 4 vertex also adjacent to a deg 3 much faster than searching thru but even so… all bijections for an isomorphism isomorphism.13 isomorphism.14 Albert R Meyer April 1, 2013 Albert R Meyer April 1, 2013 4

  5. MIT OpenCourseWare http://ocw.mit.edu 6.042J / 18.062J Mathematics for Computer Science Spring 20 15 For information about citing these materials or our Terms of Use, visit: http://ocw.mit.edu/terms.

Download Presentation
Download Policy: The content available on the website is offered to you 'AS IS' for your personal information and use only. It cannot be commercialized, licensed, or distributed on other websites without prior consent from the author. To download a presentation, simply click this link. If you encounter any difficulties during the download process, it's possible that the publisher has removed the file from their server.

Recommend

Graphs Graphs Simple graphs Algorithms Depth-first search Breadth-first search

Graphs Graphs Simple graphs Algorithms Depth-first search Breadth-first search

CS171 Introduction to Computer Science II Graphs Graphs Simple graphs Algorithms Depth-first search Breadth-first search shortest path Connected components Directed graphs Weighted graphs Minimum spanning tree

781 views • 53 slides
Graphs Graphs Simple graphs Algorithms Depth-first search Breadth-first search

Graphs Graphs Simple graphs Algorithms Depth-first search Breadth-first search

CS171 Introduction to Computer Science II Science II Graphs Graphs Simple graphs Algorithms Depth-first search Breadth-first search shortest path shortest path Connected components Directed graphs Weighted

955 views • 51 slides
Graphs Graphs Simple graphs Algorithms Depth-first search Breadth-first search

Graphs Graphs Simple graphs Algorithms Depth-first search Breadth-first search

CS171 Introduction to Computer Science II Science II Graphs Graphs Simple graphs Algorithms Depth-first search Breadth-first search shortest path shortest path Connected components Directed graphs Weighted

499 views • 32 slides
Graph coloring Kevin Ly September 20, 2019 Itinerary Introduction to simple graphs A

Graph coloring Kevin Ly September 20, 2019 Itinerary Introduction to simple graphs A

Graph coloring Kevin Ly September 20, 2019 Itinerary Introduction to simple graphs A brief game of matching The coloring problem and DSATUR Networkx demo Graphs primer A simple graph G consists of a set V and a set of pairs E .

524 views • 23 slides
Graphs 15-110 Monday 10/19 Learning Goals Identify core parts of graphs , including

Graphs 15-110 Monday 10/19 Learning Goals Identify core parts of graphs , including

Graphs 15-110 Monday 10/19 Learning Goals Identify core parts of graphs , including nodes, edges, neighbors, weights, and directions . Use graphs implemented as dictionaries when reading and writing simple algorithms in code 2

330 views • 20 slides
A Simple rule for the evolu0on of coopera0on on graphs

A Simple rule for the evolu0on of coopera0on on graphs

A Simple rule for the evolu0on of coopera0on on graphs and social networks Meat-eater ants feeding on a cicada, social PNAS: Leadership,

366 views • 5 slides
Simple dynamics on graphs Maximilien Gadouleau Durham University, UK Adrien Richard CNRS &

Simple dynamics on graphs Maximilien Gadouleau Durham University, UK Adrien Richard CNRS &

Simple dynamics on graphs Maximilien Gadouleau Durham University, UK Adrien Richard CNRS & Universit e de Nice-Sophia Antipolis Paris, Novembre 23, 2015 Gadouleau & Richard Simple Dynamics on Graphs Paris 2015 1/12 Let A = { 0 ,

832 views • 15 slides
St Andrews, September 59, 2006 Interpreting graphs in 0-simple semigroups with involution with

St Andrews, September 59, 2006 Interpreting graphs in 0-simple semigroups with involution with

St Andrews, September 59, 2006 Interpreting graphs in 0-simple semigroups with involution with applications to computational complexity and the finite basis problem Mikhail Volkov (joint work with Marcel Jackson) Ural State University,

686 views • 43 slides
St Andrews, September 59, 2006 Interpreting graphs in 0-simple semigroups with involution with

St Andrews, September 59, 2006 Interpreting graphs in 0-simple semigroups with involution with

St Andrews, September 59, 2006 Interpreting graphs in 0-simple semigroups with involution with applications to computational complexity and the finite basis problem Mikhail Volkov (joint work with Marcel Jackson) Ural State University,

1.61k views • 118 slides
Constructing universal graphs Steve Butler Department of Mathematics Iowa State University

Constructing universal graphs Steve Butler Department of Mathematics Iowa State University

Constructing universal graphs Steve Butler Department of Mathematics Iowa State University MIGHTY LII 28 April 2012 Types of graphs. Simple graphs: edges are unordered pairs of vertices (no repetitions) Directed graphs: edges are ordered

572 views • 22 slides
Graphs-Introduction November 9, 2016 CMPE 250 Graphs-Introduction November 9, 2016 1 / 32

Graphs-Introduction November 9, 2016 CMPE 250 Graphs-Introduction November 9, 2016 1 / 32

Graphs-Introduction November 9, 2016 CMPE 250 Graphs-Introduction November 9, 2016 1 / 32 Graphs - Basic Concepts Basic definitions: vertices and edges More definitions: paths, simple paths, cycles, loops Connected and disconnected graphs

484 views • 32 slides
SNA 6: processes on networks Lada Adamic Processes on networks Diffusion (simple) ER

SNA 6: processes on networks Lada Adamic Processes on networks Diffusion (simple) ER

SNA 6: processes on networks Lada Adamic Processes on networks Diffusion (simple) ER graphs Scale-free graphs Small-world topologies Complex contagion/thresholds Collective action Innovation Problem

548 views • 43 slides
Graphs () Graphs () Graphs Graphs Graphs are collections of nodes

Graphs () Graphs () Graphs Graphs Graphs are collections of nodes

Graphs () Graphs () Graphs Graphs Graphs are collections of nodes in which various pairs are connected by K08 line segments. The

627 views • 17 slides
Simple Graphs: if they remain connected k-Connectivity whenever fewer than k edges are deleted.

Simple Graphs: if they remain connected k-Connectivity whenever fewer than k edges are deleted.

Edge Connectedness Mathematics for Computer Science MIT 6.042J/18.062J Def: vertices v, w are k-edge connected Simple Graphs: if they remain connected k-Connectivity whenever fewer than k edges are deleted. Albert R Meyer, April 5, 2013

232 views • 6 slides
Graphs Graphs Examples Definitions Implementation/Representation of graphs Graphs

Graphs Graphs Examples Definitions Implementation/Representation of graphs Graphs

CS171 Introduction to Computer Science II Science II Graphs Graphs Examples Definitions Implementation/Representation of graphs Graphs Graphs: set of vertices connected pairwise by edges Interesting and useful structure

346 views • 30 slides
Strong Randomness Properties of (Hyper-)Graphs Generated by Simple Hash Functions Martin Aum

Strong Randomness Properties of (Hyper-)Graphs Generated by Simple Hash Functions Martin Aum

Strong Randomness Properties of (Hyper-)Graphs Generated by Simple Hash Functions Martin Aum uller Technische Universit at Ilmenau, Germany AofA15 Strobl, June 8, 2015 Joint work with Martin Dietzfelbinger and Philipp Woelfel. M.

691 views • 56 slides
From Saving the Princess to From Saving the Princess to Saving the Cow Saving the Cow Content

From Saving the Princess to From Saving the Princess to Saving the Cow Saving the Cow Content

From Saving the Princess to From Saving the Princess to Saving the Cow Saving the Cow Content Lessons from MMOs to Facebook Games Content Lessons from MMOs to Facebook Games Anne Toole The Write Toole Writer/Narrative Designer Who am I?

1.52k views • 39 slides
Moving toward formalisation COMP60421 Sean Bechhofer sean.bechhofer@manchester.ac.uk

Moving toward formalisation COMP60421 Sean Bechhofer sean.bechhofer@manchester.ac.uk

Moving toward formalisation COMP60421 Sean Bechhofer sean.bechhofer@manchester.ac.uk (thanks to Bijan Parsia for slides) Previously... We started the acquisition process... We elicited tacit knowledge In a variety of ways

811 views • 52 slides
CompSci 94 1) Setting up the scene Classwork: Biped Procs, Review 2D Add in any ground, I

CompSci 94 1) Setting up the scene Classwork: Biped Procs, Review 2D Add in any ground, I

CompSci 94 1) Setting up the scene Classwork: Biped Procs, Review 2D Add in any ground, I chose desert views Drag in these objects so they are in positions September 8, 2020 similar to the picture on the next page Biped: panda,

80 views • 5 slides
CS 744: MAPREDUCE Shivaram Venkataraman Fall 2019 ANNOUNCEMENTS Assignment 1 out

CS 744: MAPREDUCE Shivaram Venkataraman Fall 2019 ANNOUNCEMENTS Assignment 1 out

CS 744: MAPREDUCE Shivaram Venkataraman Fall 2019 ANNOUNCEMENTS Assignment 1 out CloudLab notes on Piazza No teams yet? Applications Machine Learning SQL Streaming Graph Computational Engines Scalable Storage Systems Resource

825 views • 24 slides
Generalizing the Kawaguchi-Kyan Bound to Stochastic Parallel Machine Scheduling Sven Jger

Generalizing the Kawaguchi-Kyan Bound to Stochastic Parallel Machine Scheduling Sven Jger

Generalizing the Kawaguchi-Kyan Bound to Stochastic Parallel Machine Scheduling Sven Jger Martin Skutella Combinatorial Optimization and Graph Algorithms Technische Universitt Berlin 22 nd Combinatorial Optimization Workshop, Aussois w

525 views • 37 slides
Write Amplification: An Analysis of In-Memory Database Durability Techniques Jaemyung Kim ,

Write Amplification: An Analysis of In-Memory Database Durability Techniques Jaemyung Kim ,

Write Amplification: An Analysis of In-Memory Database Durability Techniques Jaemyung Kim , Kenneth Salem, Khuzaima Daudjee University of Waterloo IMDM 2015 Durability Matters OLTP IMDB Orders of magnitude faster! I/O is unavoidable! (ACID,

421 views • 39 slides
Searching with turn cost and related problems Spyros Angelopoulos CNRS-UPMC Joint work with

Searching with turn cost and related problems Spyros Angelopoulos CNRS-UPMC Joint work with

Searching with turn cost and related problems Spyros Angelopoulos CNRS-UPMC Joint work with Diogo Arsenio Christoph Drr Alex Lopez-Ortiz CNRS CNRS Univ. of Waterloo Monday, April 7, 14 Outline of the presentation Monday, April 7, 14

1.43k views • 109 slides
Parallelism vs. Concurrency Key concerns Concurrency: Parallelism: Correctly

Parallelism vs. Concurrency Key concerns Concurrency: Parallelism: Correctly

12/9/15 Parallelism vs. Concurrency Key concerns Concurrency: Parallelism: Correctly and efficiently manage Use extra resources to access to shared resources solve a problem

431 views • 3 slides

More recommend