segmented regression model 11 oct 2014
play

Segmented Regression Model 11 Oct, 2014 1E 2014 NNN 1 1E 2014 - PDF document

Sep 12, 2023 •5 likes •165 views

Segmented Regression Model 11 Oct, 2014 1E 2014 NNN 1 1E 2014 NNN 2 Segmented Are Global Regression Models Temperatures Increasing Milo Schield 1 year averages Augsburg College Which source? Editor of www.StatLit.org US Rep:

  1. Segmented Regression Model 11 Oct, 2014 1E 2014 NNN 1 1E 2014 NNN 2 Segmented Are Global Regression Models Temperatures Increasing Milo Schield 1 year averages Augsburg College Which source? Editor of www.StatLit.org US Rep: International Statistical Literacy Project Surface or Fall 2014 satellite National Numeracy Network Conference based? www.StatLit.org/pdf/2014-Schield-NNN5-Slides.pdf 1E 2014 NNN 3 1E 2014 NNN 4 Are Global Surface Global Surface Temperatures: Temperatures Still Increasing Are they Still Increasing? Averaged over what time period? One-year or five? . Mean 5 year Temperature (C) Anomaly Base: 1951 ‐ 1990 Average Global Surface Temperatures (GISS): 0.65 Averages: 1 year vs 5 year 0.70 0.65 0.55 0.60 0.55 0.45 0.50 Slope: +1.6 C per 100 years Five ‐ year average: 0.45 R ‐ sq = 0.78 Two years on each side 0.40 0.35 One ‐ year average 0.35 http://data.giss.nasa.gov/gistemp/graphs_v3/ 0.30 0.25 0.25 1994 1996 1998 2000 2002 2004 2006 2008 2010 1994 1996 1998 2000 2002 2004 2006 2008 2010 2012 1E 2014 NNN 5 1E 2014 NNN 6 Minimize Total Error Using a Two-Segment Model Relative to Predicted . Least-squares regression works when data is nearly linear. Joint Std. Error in Y given X (STEYX) Rather than transform, consider a segmented linear model. 0.045 The goal is unchanged: minimum variation about model. 0.040 Best cutpoint of 0.035 two segments GISS Mean 5 year Temperature (C) Anomaly GISS Mean 5 year Temperature (C) Anomaly Cut Point: 1998 Cut Point: 2007 is at 2004 0.65 0.65 0.030 Base: 1951 ‐ 1990 Average 0.55 0.55 0.025 0.45 0.45 0.020 Joint STEYX is weighted average 0.35 of STEYX1 and STEYX2 0.35 Base: 1951 ‐ 0.015 1990 Average 0.25 0.25 1994 1996 1998 2000 2002 2004 2006 2008 2010 1994 1996 1998 2000 2002 2004 2006 2008 2010 1994 1996 1998 2000 2002 2004 2006 2008 2010 2014-Schield-NNN5-slides.pdf 1

  2. Segmented Regression Model 11 Oct, 2014 1E 2014 NNN 7 1E 2014 NNN 8 Best fit Two-Segment Model: Two-Segment Model 95% Confidence Intervals Two ‐ Segment Linear Model . . Segmented Modelling 95% Confidence Intervals 0.70 0.70 0.65 0.65 0.60 0.60 0.55 0.55 Slope: ‐ 0.3 C 0.50 0.50 per 100 years 0.45 0.45 Best cutpoint Cutpoint of of the 0.40 0.40 two segments Slope: +2.8 C two segments 0.35 0.35 at 2004 is at 2004 per 100 years 0.30 0.30 1995 1997 1999 2001 2003 2005 2007 2009 2011 1995 1997 1999 2001 2003 2005 2007 2009 2011 1E 2014 NNN 9 1E 2014 NNN 10 Is the Segmentation Conclusion Statistically Significant? Five-year averages of global surface temperatures: . Non ‐ Overlapping Confidence Intervals: Statistical Significance 0.64 From 1994-2004, they trended up: 2.8 o C per century. 0.62 Since 2004, they trended down: -0.3 o C per century 0.60 After 2008 a statistician could say: “In 2004 - 2013, 0.58 the trend in five-year averaged global surface New segment 0.56 temperatures changed from positive (2.8 C per 100 is statistically Cutpoint of 0.54 significant two segments years) to negative (-0.3 C per 100 years) and this as of 2008 at 2004 0.52 change in trend was statistically-significant.” 2001 2002 2003 2004 2005 2006 2007 2008 2009 1E 2014 NNN 11 1E 2014 NNN 12 Create Line 2 Series; DATA LINE1 LINE1 Create Line1 Year Ave5yr b1 STEYX1 Calculate Joint STEYX 1994 0.29 1995 0.34 0.050 1996 0.42 0.065 0.012 Out of DATA LINE1 LINE1 LINE2 LINE2 Joint 1. Current row = 1995. 1997 0.45 0.056 0.014 Year Ave5yr b1 STEYX1 b2 STEYX2 STEYX control? 1998 0.44 0.041 0.030 1994 0.29 0.015 0.045 0.0452 2. Fit 5 year data from 1995 0.34 0.050 0.013 0.038 0.0371 1999 0.48 0.037 0.028 1994 to current row. 1996 0.42 0.065 0.012 0.011 0.031 0.0299 2000 0.51 0.034 0.026 1997 0.45 0.056 0.014 0.011 0.031 0.0288 3. Calculate slope b1 using 2001 0.51 0.030 0.028 1998 0.44 0.041 0.030 0.010 0.031 0.0310 2002 0.53 0.028 0.028 1999 0.48 0.037 0.028 0.008 0.028 0.0277 Excel SLOPE. 2000 0.51 0.034 0.026 0.006 0.026 0.0258 2003 0.58 0.028 0.026 3. Calculate Std. Error of Y 2001 0.51 0.030 0.028 0.005 0.025 0.0262 2004 0.60 0.028 0.025 2002 0.53 0.028 0.028 0.002 0.020 0.0242 given X using Excel 2005 0.60 0.026 0.025 2003 0.58 0.028 0.026 ‐ 0.001 0.010 0.0202 STEYX. 2004 0.60 0.028 0.025 ‐ 0.003 0.009 0.0198 2006 0.58 0.024 0.030 2005 0.60 0.026 0.025 ‐ 0.002 0.009 0.0209 2007 0.59 0.022 0.033 4. Increase current row; 2006 0.58 0.024 0.030 ‐ 0.001 0.009 0.0256 2008 0.59 0.020 0.036 2007 0.59 0.022 0.033 ‐ 0.002 0.010 0.0291 Repeat 2, 3 & 4. 2009 0.58 0.019 0.040 2008 0.59 0.020 0.036 ‐ 0.001 0.012 0.0328 2010 0.57 0.017 0.044 2009 0.58 0.019 0.040 0.005 0.012 0.0375 Out-of-control??? 2010 0.57 0.017 0.044 0.020 0.0425 2011 0.59 0.015 0.045 2011 0.59 0.015 0.045 0.0452 2014-Schield-NNN5-slides.pdf 2

  3. Segmented Regression Model 11 Oct, 2014 1E 2014 NNN 13 References Wikipedia: Change Detection Wikipedia: Time-series segmentation Wikipedia: Time Series [Segmentation] Wikipedia: Regression Analysis 2014-Schield-NNN5-slides.pdf 3

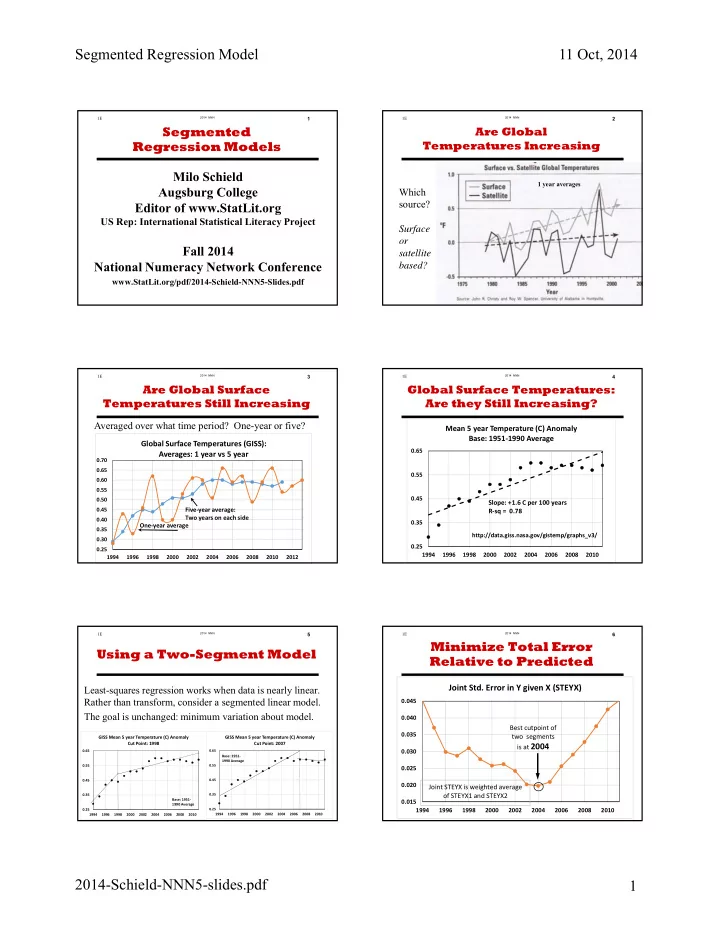
  4. 1E 2014 NNN 1 Segmented Regression Models Milo Schield Augsburg College Editor of www.StatLit.org US Rep: International Statistical Literacy Project Fall 2014 National Numeracy Network Conference www.StatLit.org/pdf/2014-Schield-NNN5-Slides.pdf

  5. 1E 2014 NNN 2 Are Global Temperatures Increasing 1 year averages Which source? Surface or satellite based?

  6. 1E 2014 NNN 3 Are Global Surface Temperatures Still Increasing Averaged over what time period? One-year or five? Global Surface Temperatures (GISS): Averages: 1 year vs 5 year 0.70 0.65 0.60 0.55 0.50 0.45 Five ‐ year average: Two years on each side 0.40 One ‐ year average 0.35 0.30 0.25 1994 1996 1998 2000 2002 2004 2006 2008 2010 2012

  7. 1E 2014 NNN 4 Global Surface Temperatures: Are they Still Increasing? . Mean 5 year Temperature (C) Anomaly Base: 1951 ‐ 1990 Average 0.65 0.55 0.45 Slope: +1.6 C per 100 years R ‐ sq = 0.78 0.35 http://data.giss.nasa.gov/gistemp/graphs_v3/ 0.25 1994 1996 1998 2000 2002 2004 2006 2008 2010

  8. 1E 2014 NNN 5 Using a Two-Segment Model Least-squares regression works when data is nearly linear. Rather than transform, consider a segmented linear model. The goal is unchanged: minimum variation about model. GISS Mean 5 year Temperature (C) Anomaly GISS Mean 5 year Temperature (C) Anomaly Cut Point: 1998 Cut Point: 2007 0.65 0.65 Base: 1951 ‐ 1990 Average 0.55 0.55 0.45 0.45 0.35 0.35 Base: 1951 ‐ 1990 Average 0.25 0.25 1994 1996 1998 2000 2002 2004 2006 2008 2010 1994 1996 1998 2000 2002 2004 2006 2008 2010

  9. 1E 2014 NNN 6 Minimize Total Error Relative to Predicted . Joint Std. Error in Y given X (STEYX) 0.045 0.040 Best cutpoint of 0.035 two segments is at 2004 0.030 0.025 0.020 Joint STEYX is weighted average of STEYX1 and STEYX2 0.015 1994 1996 1998 2000 2002 2004 2006 2008 2010

  10. 1E 2014 NNN 7 Best fit Two-Segment Model . Two ‐ Segment Linear Model 0.70 0.65 0.60 0.55 Slope: ‐ 0.3 C 0.50 per 100 years 0.45 Best cutpoint of the 0.40 Slope: +2.8 C two segments 0.35 is at 2004 per 100 years 0.30 1995 1997 1999 2001 2003 2005 2007 2009 2011

  11. 1E 2014 NNN 8 Two-Segment Model: 95% Confidence Intervals . Segmented Modelling 95% Confidence Intervals 0.70 0.65 0.60 0.55 0.50 0.45 Cutpoint of 0.40 two segments 0.35 at 2004 0.30 1995 1997 1999 2001 2003 2005 2007 2009 2011

  12. 1E 2014 NNN 9 Is the Segmentation Statistically Significant? . Non ‐ Overlapping Confidence Intervals: Statistical Significance 0.64 0.62 0.60 0.58 New segment 0.56 is statistically Cutpoint of 0.54 significant two segments as of 2008 at 2004 0.52 2001 2002 2003 2004 2005 2006 2007 2008 2009

  13. 1E 2014 NNN 10 Conclusion Five-year averages of global surface temperatures: From 1994-2004, they trended up: 2.8 o C per century. Since 2004, they trended down: -0.3 o C per century After 2008 a statistician could say: “In 2004 - 2013, the trend in five-year averaged global surface temperatures changed from positive (2.8 C per 100 years) to negative (-0.3 C per 100 years) and this change in trend was statistically-significant.”

  14. 1E 2014 NNN 11 DATA LINE1 LINE1 Create Line1 Year Ave5yr b1 STEYX1 1994 0.29 1995 0.34 0.050 1996 0.42 0.065 0.012 1. Current row = 1995. 1997 0.45 0.056 0.014 1998 0.44 0.041 0.030 2. Fit 5 year data from 1999 0.48 0.037 0.028 1994 to current row. 2000 0.51 0.034 0.026 2001 0.51 0.030 0.028 3. Calculate slope b1 using 2002 0.53 0.028 0.028 Excel SLOPE. 2003 0.58 0.028 0.026 3. Calculate Std. Error of Y 2004 0.60 0.028 0.025 given X using Excel 2005 0.60 0.026 0.025 STEYX. 2006 0.58 0.024 0.030 2007 0.59 0.022 0.033 4. Increase current row; 2008 0.59 0.020 0.036 Repeat 2, 3 & 4. 2009 0.58 0.019 0.040 2010 0.57 0.017 0.044 Out-of-control??? 2011 0.59 0.015 0.045

Recommend

A comparison of estimators for regression models with change points Cathy WS Chen 1 , Jennifer SK

A comparison of estimators for regression models with change points Cathy WS Chen 1 , Jennifer SK

Aim Change-points Bayesian Julious Segmented Grid search Simulation Return prediction model Applications Conclusions A comparison of estimators for regression models with change points Cathy WS Chen 1 , Jennifer SK Chan 2 , Richard

1.44k views • 42 slides
Multiple Linear Regression The population model In a simple linear regression model, a single

Multiple Linear Regression The population model In a simple linear regression model, a single

Multiple Linear Regression The population model In a simple linear regression model, a single response measure- ment Y is related to a single predictor (covariate, regressor) X for each observation. The critical assumption of the model is

859 views • 49 slides
Logistic Regression James H. Steiger Department of Psychology and Human Development Vanderbilt

Logistic Regression James H. Steiger Department of Psychology and Human Development Vanderbilt

Introduction The Logistic Regression Model Binary Logistic Regression Binomial Logistic Regression Interpreting Logistic Regression Parameters Examples Logistic Regression and Retrospective Studies Logistic Regression James H. Steiger

777 views • 54 slides
Regression Diagnostics Introduction to Regression 1 Why do we need to do all this? Theory

Regression Diagnostics Introduction to Regression 1 Why do we need to do all this? Theory

Regression Diagnostics Introduction to Regression 1 Why do we need to do all this? Theory based on assumptions Focuses on the residuals and fitted values Validate the model Gives us clues how to change the model Is it

575 views • 44 slides
Hypothesis Testing in Regression Models Recall the regression model: y = 0 + 1 x 1 + 2 x

Hypothesis Testing in Regression Models Recall the regression model: y = 0 + 1 x 1 + 2 x

ST 516 Experimental Statistics for Engineers II Hypothesis Testing in Regression Models Recall the regression model: y = 0 + 1 x 1 + 2 x 2 + + k x k + . Test for significance of regression: H 0 : 1 = 2 = =

491 views • 18 slides
Simple Linear Regression Recall: A regression model describes how a dependent variable (or

Simple Linear Regression Recall: A regression model describes how a dependent variable (or

ST 430/514 Introduction to Regression Analysis/Statistics for Management and the Social Sciences II Simple Linear Regression Recall: A regression model describes how a dependent variable (or response ) Y is affected, on average, by one or more

592 views • 20 slides
Multiple Linear Regression Recall: a regression model describes how a dependent variable (or

Multiple Linear Regression Recall: a regression model describes how a dependent variable (or

ST 430/514 Introduction to Regression Analysis/Statistics for Management and the Social Sciences II Multiple Linear Regression Recall: a regression model describes how a dependent variable (or response ) Y is affected, on average, by one or more

526 views • 21 slides
Assessing model fit Correlation and Regression How well does our textbook model fit? >

Assessing model fit Correlation and Regression How well does our textbook model fit? >

CORRELATION AND REGRESSION Assessing model fit Correlation and Regression How well does our textbook model fit? > ggplot(data = textbooks, aes(x = amazNew, y = uclaNew)) + geom_point() + geom_smooth(method = "lm", se = FALSE)

914 views • 43 slides
Logistic Regression Lecture 6 Logistic Regression Classification Model CS 335

Logistic Regression Lecture 6 Logistic Regression Classification Model CS 335

Logistic Regression Lecture 6 Logistic Regression Classification Model CS 335 Cost function Gradient descent Linear classifiers and decision boundaries Dan Sheldon Classification Example: Hand-Written Digits Input: 20

541 views • 5 slides
Applied Statistics Lecturer: Serena Arima Regression model Model estimation Properties OLS

Applied Statistics Lecturer: Serena Arima Regression model Model estimation Properties OLS

Regression model Model estimation Properties OLS estimator Applied Statistics Lecturer: Serena Arima Regression model Model estimation Properties OLS estimator Linear regression model Consider the income and the expenditure of a sample of n

762 views • 51 slides
Overview IAML: Linear Regression The linear model Fitting the linear model to data

Overview IAML: Linear Regression The linear model Fitting the linear model to data

Overview IAML: Linear Regression The linear model Fitting the linear model to data Probabilistic interpretation of the error function Nigel Goddard School of Informatics Examples of regression problems Dealing with multiple

325 views • 10 slides
Resid u als from regression model FOR E C ASTIN G P R OD U C T D E MAN D IN R Aric LaBarr , Ph

Resid u als from regression model FOR E C ASTIN G P R OD U C T D E MAN D IN R Aric LaBarr , Ph

Resid u als from regression model FOR E C ASTIN G P R OD U C T D E MAN D IN R Aric LaBarr , Ph . D . Senior Data Scientist , Elder Research Linear Regression FORECASTING PRODUCT DEMAND IN R Regression Resid u als Wa y s to red u ce resid u

667 views • 23 slides
Multiple and Logistic Regression IV Dajiang Liu @PHS 525 Apr-21 st -2016 Review of Last Two

Multiple and Logistic Regression IV Dajiang Liu @PHS 525 Apr-21 st -2016 Review of Last Two

Multiple and Logistic Regression IV Dajiang Liu @PHS 525 Apr-21 st -2016 Review of Last Two Classes Linear regression model: Logistic regression model Deal with binary outcomes Why is multiple (simple) linear regression model

260 views • 15 slides
0 Regression Model Development and Yet Another Regression Function Werner Stahel Seminar f u

0 Regression Model Development and Yet Another Regression Function Werner Stahel Seminar f u

0 Regression Model Development and Yet Another Regression Function Werner Stahel Seminar f u r Statistik, ETH Z u rich useR 2008, Dortmund 1 Data Analysis ... needs a system that gives MORE support. I show you such a system for

322 views • 21 slides
Introduction to Regression Analysis Modeling a Response A regression model describes how a

Introduction to Regression Analysis Modeling a Response A regression model describes how a

ST 430/514 Introduction to Regression Analysis/Statistics for Management and the Social Sciences II Introduction to Regression Analysis Modeling a Response A regression model describes how a dependent variable (or response ) Y is affected, on

575 views • 13 slides
Inverse Prediction One use of a regression model E ( Y ) = 0 + 1 x is to predict Y for a new

Inverse Prediction One use of a regression model E ( Y ) = 0 + 1 x is to predict Y for a new

ST 430/514 Introduction to Regression Analysis/Statistics for Management and the Social Sciences II Inverse Prediction One use of a regression model E ( Y ) = 0 + 1 x is to predict Y for a new x , x 0 . Sometimes, instead, we observe a new

236 views • 4 slides
Supervised Learning Regression, Classifica6on Linear regression,

Supervised Learning Regression, Classifica6on Linear regression,

Supervised Learning Regression, Classifica6on Linear regression, k- NN classifica6on Debapriyo Majumdar Data Mining Fall 2014 Indian Statistical Institute Kolkata August 11, 2014 An Example:

621 views • 24 slides
Slide Set 3 Notes Regression Models and the Classical Linear Regression Model (CLRM) Pietro

Slide Set 3 Notes Regression Models and the Classical Linear Regression Model (CLRM) Pietro

Slide Set 3 Notes Regression Models and the Classical Linear Regression Model (CLRM) Pietro Coretto pcoretto@unisa.it Econometrics Master in Economics and Finance (MEF) Universit degli Studi di Napoli Federico II Version: Tuesday 21

478 views • 13 slides
BS2247 Introduction to Econometrics Lecture 3: The simple regression model OLS, Algebraic

BS2247 Introduction to Econometrics Lecture 3: The simple regression model OLS, Algebraic

BS2247 Introduction to Econometrics Lecture 3: The simple regression model OLS, Algebraic properties, Goodness-of-fit Dr. Kai Sun Aston Business School 1 / 28 The Simple Regression Model: y = 0 + 1 x + u In the simple linear regression of

708 views • 54 slides
Multiple Regression Peerapat Wongchaiwat, Ph.D. wongchaiwat@hotmail.com The Multiple Regression

Multiple Regression Peerapat Wongchaiwat, Ph.D. wongchaiwat@hotmail.com The Multiple Regression

Multiple Regression Peerapat Wongchaiwat, Ph.D. wongchaiwat@hotmail.com The Multiple Regression Model Examine the linear relationship between 1 dependent (Y) & 2 or more independent variables (X i ) Multiple Regression Model with k

821 views • 47 slides
Recall: Linear Regression 200 180 160 140 Power (bhp)

Recall: Linear Regression 200 180 160 140 Power (bhp)

Logis&c Regression Debapriyo Majumdar Data Mining Fall 2014 Indian Statistical Institute Kolkata September 1, 2014 Recall: Linear Regression 200 180 160 140 Power (bhp) 120

561 views • 19 slides
Multiple Linear Regression James H. Steiger Department of Psychology and Human Development

Multiple Linear Regression James H. Steiger Department of Psychology and Human Development

Introduction The Multiple Regression Model Setting Up a Multiple Regression Model Multiple Linear Regression James H. Steiger Department of Psychology and Human Development Vanderbilt University Multilevel Regression Modeling, 2009

709 views • 41 slides
The Foundation of Regression Analysis Bivariate Linear Regression James H. Steiger Department of

The Foundation of Regression Analysis Bivariate Linear Regression James H. Steiger Department of

The Classic Bivariate Least Squares Model Evaluating and Extending the Model The Foundation of Regression Analysis Bivariate Linear Regression James H. Steiger Department of Psychology and Human Development Vanderbilt University Multilevel

1.36k views • 112 slides
EC3062 ECONOMETRICS THE MULTIPLE REGRESSION MODEL Consider T realisations of the regression

EC3062 ECONOMETRICS THE MULTIPLE REGRESSION MODEL Consider T realisations of the regression

EC3062 ECONOMETRICS THE MULTIPLE REGRESSION MODEL Consider T realisations of the regression equation (1) y = 0 + 1 x 1 + + k x k + , which can be written in the following form: y 1 0 1 x 11 . . . x 1 k 1

456 views • 34 slides

More recommend