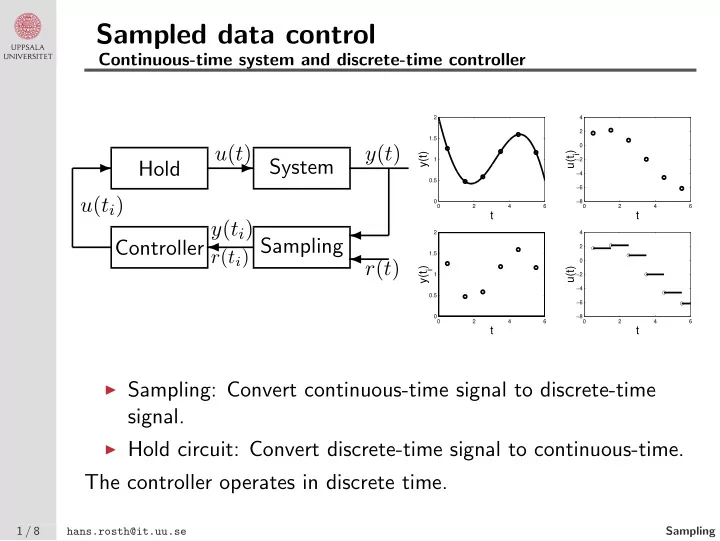
Sampled data control Continuous-time system and discrete-time - PowerPoint PPT Presentation

Sampled data control Continuous-time system and discrete-time controller 2 4 2 1.5 u ( t ) y ( t ) 0 u(t i ) y(t) System 1 −2 Hold ✲ ✲ −4 0.5 −6 u ( t i ) 0 −8 0 2 4 6 0 2 4 6 t t y ( t i ) 2 4 ✛ Sampling Controller ✛ 2 r ( t i ) 1.5 ✛ r ( t ) 0 y(t i ) u(t) 1 −2 −4 0.5 −6 0 −8 0 2 4 6 0 2 4 6 t t ◮ Sampling: Convert continuous-time signal to discrete-time signal. ◮ Hold circuit: Convert discrete-time signal to continuous-time. The controller operates in discrete time. 1 / 8 hans.rosth@it.uu.se Sampling

Aliasing Can a continuous-time signal be reconstructed from discrete-time data? Sampling period h = 1 time unit. 1 0 −1 2 4 6 8 time The two sinusoids (solid and dashed lines) cannot be distinguished from each other by the sampled signal (rings). 2 / 8 hans.rosth@it.uu.se Sampling

Examples of sampled systems The harmonic oscillator ◮ Continuous-time system: � � � �  0 − 1 1  x = ˙ x + u,  1  1 0 0 Y ( s ) = s 2 + 1 U ( s ) ⇔ � �   y = 0 1 x  ◮ Discrete-time state space model: � � � �  cos( h ) − sin( h ) sin( h )  x ( k + 1) = x ( k ) + u ( k ) ,   sin( h ) cos( h ) 1 − cos( h ) � �  y ( k ) = x ( k ) .  0 1  ◮ Discrete-time transfer function: G ( z ) = H ( zI − F ) − 1 G = (1 − cos( h ))( z + 1) z 2 − 2 cos( h ) z + 1 3 / 8 hans.rosth@it.uu.se Sampling

Examples of sampled systems The double integrator ◮ Continuous-time system: � � � �  0 0 1  x = ˙ x + u,  Y ( s ) = 1  1 0 0 s 2 U ( s ) ⇔ � �   y = 0 1 x  ◮ Discrete-time state space model: � � � �  1 0 h  x ( k + 1) = x ( k ) + u ( k ) ,   0 . 5 h 2 1 h � �   y ( k ) = 0 1 x ( k ) .  ◮ Discrete-time transfer function: � − 1 � = 0 . 5 h 2 ( z + 1) � � z − 1 � 0 h � G ( z ) = 0 1 0 . 5 h 2 − h z − 1 ( z − 1) 2 4 / 8 hans.rosth@it.uu.se Sampling

Examples of sampled systems DC motor ◮ Continuous-time system: � � � �  0 0 1  x = ˙ x + u,  1  0 − 1 1 Y ( s ) = s ( s + 1) U ( s ) ⇔ � �   y = 1 − 1 x  ◮ Discrete-time state space model: � � � �  1 0 h  x ( k + 1) = x ( k ) + u ( k ) ,   e − h 1 − e − h 0 � �  y ( k ) = x ( k ) .  1 − 1  ◮ Discrete-time transfer function: G ( z ) = H ( zI − F ) − 1 G = ( h − 1 + e − h ) z + 1 − (1 + h ) e − h ( z − 1)( z − e − h ) ◮ Zero in z ′ = − 1 − (1+ h ) e − h h − 1+ e − h , and − 1 < z ′ < 0 for h > 0 . 5 / 8 hans.rosth@it.uu.se Sampling

Continuous-time and sampled poles How ZOH sampling maps the poles cont. time discrete time 1 0.5 0 0 −0.5 −1 0 −1 0 1 1 0.5 0 0 −0.5 −1 0 −1 0 1 1 0.5 0 0 −0.5 −1 0 −1 0 1 6 / 8 hans.rosth@it.uu.se Sampling

Frequency response of a sampled systems Piecewise constant sinusoids! 1 0.5 0 −0.5 −1 0 10 20 30 40 50 1 0.5 0 −0.5 −1 0 10 20 30 40 50 time 7 / 8 hans.rosth@it.uu.se Sampling

Frequency response for sampled systems Comparison with the continuous-time frequency response 1 Example: Y ( s ) = s 2 + s +1 U ( s ) sampled with sampling period h = 0.1 sec, 0.5 sec, 1 sec, 2 sec. 0 0 10 h = 2 sec −1 10 −90 Phase Continuous−time Gain h = 1 sec system continuous−time −2 10 system −180 h = 0.5 sec −3 10 h = 2 sec h = 0.1 sec h = 1 sec h = 0.5 sech = 0.1 sec −4 −270 10 −2 −1 0 1 2 −2 −1 0 1 2 10 10 10 10 10 10 10 10 10 10 Frequency (rad/sec) Frequency (rad/sec) Corresponding Nyquist frequencies: ω n = 31.4 rad/sec, 6.28 rad/sec, 3.14 rad/sec, 1.57 rad/s. 8 / 8 hans.rosth@it.uu.se Sampling