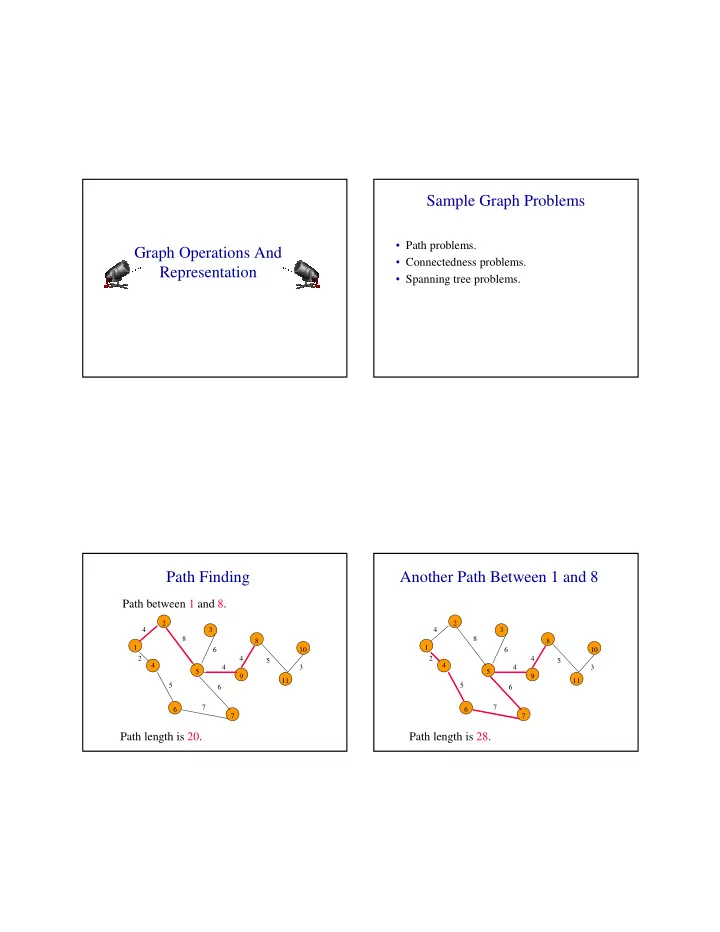
Sample Graph Problems Path problems. Graph Operations And - PDF document

Sample Graph Problems • Path problems. Graph Operations And • Connectedness problems. Representation • Spanning tree problems. Path Finding Another Path Between 1 and 8 Path between 1 and 8. 2 2 4 3 4 3 8 8 8 8 1 1 6 10 6 10 2 4 2 4 5 5 4 4 4 3 4 3 5 5 9 9 11 11 5 5 6 6 7 7 6 6 7 7 Path length is 20. Path length is 28.

Example Of No Path Connected Graph 2 • Undirected graph. 3 8 • There is a path between every pair of 1 10 vertices. 4 5 9 11 6 7 No path between 2 and 9. Example Of Not Connected Connected Graph Example 2 2 3 3 8 8 1 1 10 10 4 4 5 5 9 9 11 11 6 6 7 7

Connected Components Connected Component 2 • A maximal subgraph that is connected. 3 8 � Cannot add vertices and edges from original 1 10 graph and retain connectedness. 4 5 • A connected graph has exactly 1 9 11 component. 6 7 Not A Component Communication Network 2 2 3 3 8 8 1 1 10 10 4 4 5 5 9 9 11 11 6 6 7 7 Each edge is a link that can be constructed (i.e., a feasible link).

Communication Network Problems Cycles And Connectedness 2 • Is the network connected? 3 8 � Can we communicate between every pair of 1 10 cities? 4 5 • Find the components. 9 11 • Want to construct smallest number of feasible links so that resulting network is 6 7 connected. Removal of an edge that is on a cycle does not affect connectedness. Cycles And Connectedness Tree 2 • Connected graph that has no cycles. 3 8 • n vertex connected graph with n-1 edges. 1 10 4 5 9 11 6 7 Connected subgraph with all vertices and minimum number of edges has no cycles.

Spanning Tree Minimum Cost Spanning Tree 2 • Subgraph that includes all vertices of the 4 3 8 8 original graph. 1 6 10 2 4 • Subgraph is a tree. 5 4 4 3 5 � If original graph has n vertices, the spanning 9 8 11 5 6 tree has n vertices and n-1 edges. 2 7 6 7 • Tree cost is sum of edge weights/costs. A Spanning Tree Minimum Cost Spanning Tree 2 2 4 3 4 3 8 8 8 8 1 1 6 10 6 10 2 4 2 4 5 5 4 4 4 3 4 3 5 5 9 9 8 11 8 11 5 5 6 6 2 2 7 7 6 6 7 7 Spanning tree cost = 51. Spanning tree cost = 41.

A Wireless Broadcast Tree Graph Representation 2 • Adjacency Matrix 4 3 8 8 • Adjacency Lists 1 6 10 2 4 5 � Linked Adjacency Lists 4 4 3 5 9 � Array Adjacency Lists 8 11 5 6 2 7 6 7 Source = 1, weights = needed power. Cost = 4 + 8 + 5 + 6 + 7 + 8 + 3 = 41. Adjacency Matrix Adjacency Matrix Properties • 0/1 n x n matrix, where n = # of vertices 1 2 3 4 5 2 • A(i,j) = 1 iff (i,j) is an edge 1 0 1 0 1 0 3 2 1 0 0 0 1 1 3 0 0 0 0 1 4 4 1 0 0 0 1 5 1 2 3 4 5 5 0 1 1 1 0 2 1 0 1 0 1 0 3 •Diagonal entries are zero. 2 1 0 0 0 1 1 3 0 0 0 0 1 •Adjacency matrix of an undirected graph is 4 4 1 0 0 0 1 5 symmetric. 5 0 1 1 1 0 � A(i,j) = A(j,i) for all i and j.

Adjacency Matrix (Digraph) Adjacency Matrix 1 2 3 4 5 2 • n 2 bits of space 1 0 0 0 1 0 3 2 1 0 0 0 1 • For an undirected graph, may store only 1 3 0 0 0 0 0 lower or upper triangle (exclude diagonal). 4 4 0 0 0 0 1 5 � (n-1)n/2 bits 5 0 1 1 0 0 • O(n) time to find vertex degree and/or •Diagonal entries are zero. vertices adjacent to a given vertex. •Adjacency matrix of a digraph need not be symmetric. Adjacency Lists Linked Adjacency Lists • Adjacency list for vertex i is a linear list of • Each adjacency list is a chain. vertices adjacent from vertex i. 2 aList[1] 2 4 3 • An array of n adjacency lists. [2] 1 5 [3] 5 1 aList[1] = (2,4) [4] 5 1 4 aList[5] 2 4 3 aList[2] = (1,5) 2 5 3 aList[3] = (5) 1 aList[4] = (5,1) Array Length = n 4 5 aList[5] = (2,4,3) # of chain nodes = 2e (undirected graph) # of chain nodes = e (digraph)

Array Adjacency Lists Weighted Graphs • Each adjacency list is an array list. • Cost adjacency matrix. 2 aList[1] 2 4 3 � C(i,j) = cost of edge (i,j) [2] 1 5 [3] 5 1 • Adjacency lists => each list element is a [4] 5 1 pair (adjacent vertex, edge weight) 4 aList[5] 2 4 3 5 Array Length = n # of list elements = 2e (undirected graph) # of list elements = e (digraph) Number Of Java Classes Needed Abstract Class Graph • Graph representations package dataStructures; � Adjacency Matrix import java.util.*; � Adjacency Lists public abstract class Graph � Linked Adjacency Lists { � Array Adjacency Lists // ADT methods come here � 3 representations • Graph types � Directed and undirected. // create an iterator for vertex i � Weighted and unweighted. public abstract Iterator iterator(int i); � 2 x 2 = 4 graph types • 3 x 4 = 12 Java classes // implementation independent methods come here }

Abstract Methods Of Graph // ADT methods public abstract int vertices(); public abstract int edges(); public abstract boolean existsEdge(int i, int j); public abstract void putEdge(Object theEdge); public abstract void removeEdge(int i, int j); public abstract int degree(int i); public abstract int inDegree(int i); public abstract int outDegree(int i);