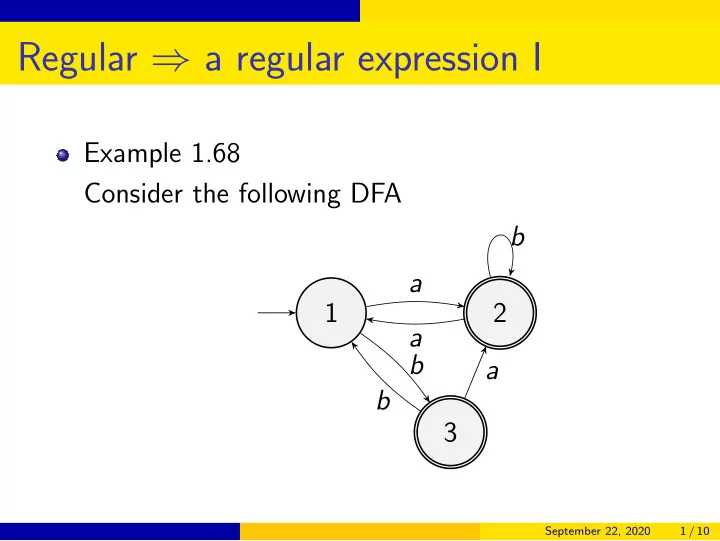
Regular a regular expression I Example 1.68 Consider the following - PowerPoint PPT Presentation

Regular ⇒ a regular expression I Example 1.68 Consider the following DFA b a 1 2 a b a b 3 September 22, 2020 1 / 10

Regular ⇒ a regular expression II It is not that easy to directly see what the regular expression is We need a procedure shown below First, add a start and an accept states b a 1 2 a ǫ ǫ b a b s a 3 ǫ September 22, 2020 2 / 10

Regular ⇒ a regular expression III This generates a generalized NFA (GNFA) Our procedure is DFA → GNFA → regular expression Remove state 1 September 22, 2020 3 / 10

Regular ⇒ a regular expression IV 2 aa ∪ b a ǫ s a ba ∪ a ab b ǫ 3 bb Example: the link 3 → 2 September 22, 2020 4 / 10

Regular ⇒ a regular expression V a 3 2 a b 1 Thus ba ∪ a Idea: now 1 is removed. Need to check how we can go from 3 to 2 via state 1 Need to check all pairs of states Remove state 2 September 22, 2020 5 / 10

Regular ⇒ a regular expression VI a ( aa ∪ b ) ∗ s a ( ba ∪ a )( aa ∪ b ) ∗ ∪ ǫ a ( aa ∪ b ) ∗ ab ∪ b 3 ( ba ∪ a )( aa ∪ b ) ∗ ab ∪ bb Example: s → 3 September 22, 2020 6 / 10

Regular ⇒ a regular expression VII b s 3 a ab 2 aa ∪ b Thus a ( aa ∪ b ) ∗ ab ∪ b September 22, 2020 7 / 10

Regular ⇒ a regular expression VIII Here we need to handle aa ∪ b 2 − − → 2 Thus in the early example of removing state 1, we actually have September 22, 2020 8 / 10

Regular ⇒ a regular expression IX a 3 2 a b 1 ∅ and b ∅ ∗ a ∪ a = b ǫ a ∪ a = ba ∪ a Remove state 3 September 22, 2020 9 / 10

Regular ⇒ a regular expression X s a ( a ( aa ∪ b ) ∗ ab ∪ b )(( ba ∪ a )( aa ∪ b ) ∗ ab ∪ bb ) ∗ (( ba ∪ a )( aa ∪ b ) ∗ ∪ ǫ ) ∪ a ( aa ∪ b ) ∗ We will formally explain the procedure September 22, 2020 10 / 10