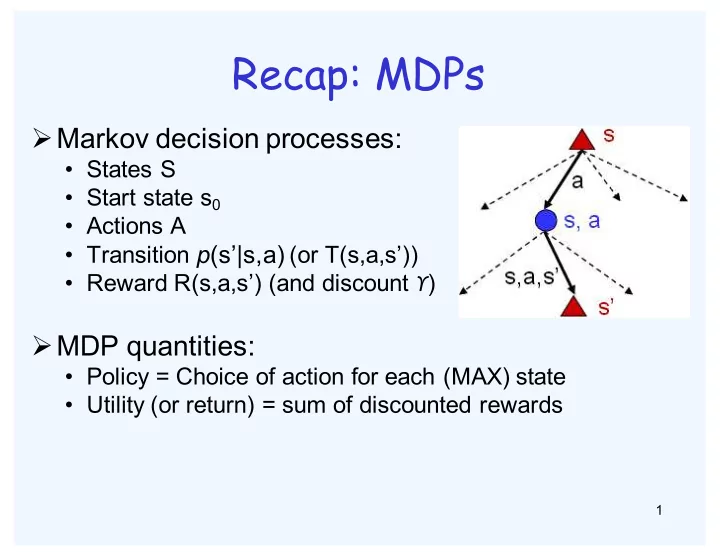
Recap: MDPs Markov decision processes: States S Start state s 0 - PowerPoint PPT Presentation

Recap: MDPs Ø Markov decision processes: • States S • Start state s 0 • Actions A • Transition p (s’|s,a) (or T(s,a,s’)) • Reward R(s,a,s’) (and discount ϒ ) Ø MDP quantities: • Policy = Choice of action for each (MAX) state • Utility (or return) = sum of discounted rewards 1

Optimal Utilities Ø The value of a state s: • V*(s) = expected utility starting in s and acting optimally Ø The value of a Q-state (s,a): • Q*(s,a) = expected utility starting in s, taking action a and thereafter acting optimally Ø The optimal policy: • π *(s) = optimal action from state s

Solving MDPs Ø Value iteration • Start with V 1 (s) = 0 • Given V i , calculate the values for all states for depth i+1: V s max T s a s , , ' R s a s , , ' V s ' ( ) ( ) ( ) ( ) ∑ ← ⎡ + γ ⎤ ⎣ ⎦ i 1 i + a s ' • Repeat until converge • Use V i as evaluation function when computing V i+ 1 Ø Policy iteration • Step 1: policy evaluation: calculate utilities for some fixed policy • Step 2: policy improvement: update policy using one-step look-ahead with resulting utilities as future values • Repeat until policy converges 3

Reinforcement learning Ø Don’t know T and/or R, but can observe R • Learn by doing • can have multiple trials 4

The Story So Far: MDPs and RL Things we know how to do: Techniques: Ø If we know the MDP • Computation • Compute V*, Q*, π* exactly • Value and policy • Evaluate a fixed policy π iteration Ø If we don’t know T and R • Policy evaluation • If we can estimate the MDP then • Model-based RL solve • sampling • We can estimate V for a fixed policy π • Model-free RL: • We can estimate Q*(s,a) for the • Q-learning optimal policy while executing an exploration policy 5

Model-Free Learning Ø Model-free (temporal difference) learning • Experience world through trials (s,a,r,s’,a’,r’,s’’,a’’,r’’,s’’’…) • Update estimates each transition (s,a,r,s’) • Over time, updates will mimic Bellman updates Q-Value Iteration (model-based, requires known MDP) ⎡ ⎤ Q s a , T s a s , , ' R s a s , , ' max Q s a ', ' ( ) ( ) ( ) ( ) ∑ ← + γ i 1 i + ⎣ ⎦ a ' s ' Q-Learning (model-free, requires only experienced transitions) ⎡ ⎤ Q s a ( , ) (1 ) ( , ) Q s a r max Q s a ', ' ( ) ← − α + α + γ ⎣ ⎦ a ' 6

Q-Learning Ø Q-learning produces tables of q-values: 7

Exploration / Exploitation Ø R andom actions (ε greedy) • Every time step, flip a coin • With probability ε, act randomly • With probability 1-ε, act according to current policy 8

Today: Q-Learning with state abstraction Ø In realistic situations, we cannot possibly learn about every single state! • Too many states to visit them all in training • Too many states to hold the Q-tables in memory Ø Instead, we want to generalize: • Learn about some small number of training states from experience • Generalize that experience to new, similar states • This is a fundamental idea in machine learning, and we’ll see it over and over again 9

Example: Pacman Ø Let’s say we discover through experience that this state is bad: Ø In naive Q-learning, we know nothing about this state or its Q-states: Ø Or even this one! 10

Feature-Based Representations Ø Solution: describe a state using a vector of features (properties) • Features are functions from states to real numbers (often 0/1) that capture important properties of the state • Example features: • Distance to closest ghost • Distance to closest dot • Number of ghosts • 1/ (dist to dot) 2 Similar to a evaluation function • Is Pacman in a tunnel? (0/1) • …etc • Can also describe a Q-state (s,a) with features (e.g. action moves closer to food) 11

Linear Feature Functions Ø Using a feature representation, we can write a Q function for any state using a few weights: ( ) = w 1 f 1 s , a ( ) + w 2 f 2 s , a ( ) +  + w n f n s , a ( ) Q s , a Ø Advantage: more efficient learning from samples Ø Disadvantage: states may share features but actually be very different in value! 12

Function Approximation ( ) = w 1 f 1 s , a ( ) + w 2 f 2 s , a ( ) +  + w n f n s , a ( ) Q s , a Ø Q-learning with linear Q-functions: transition = (s,a,r,s’) ⎡ ⎤ difference r max Q s a ', ' Q s a ( , ) ( ) = + γ − ⎣ ⎦ a ' Exact Q’s " $ Q ( s , a ) ← Q ( s , a ) + α difference # % Approximate Q’s " $ ( ) w i ← w i + α difference % f i s , a # Ø Intuitive interpretation: • Adjust weights of active features • E.g. if something unexpectedly bad happens, disprefer all states with that state’s features 13

Example: Q-Pacman s Q ( s,a ) = 4.0 f DOT ( s,a ) - 1.0 f GST ( s,a ) f DOT ( s, NORTH)=0.5 f GST ( s, NORTH)=1.0 Q ( s,a )=+1 a = North R ( s,a,s’ )=-500 r = -500 s’ difference =-501 w DOT ← 4.0+ α [-501]0.5 w GST ← -1.0+ α [-501]1.0 Q ( s,a ) = 3.0 f DOT ( s,a ) - 3.0 f GST ( s,a ) 14

Linear Regression prediction prediction  = w 0 + w 1 f 1 x  = w 0 + w 1 f 1 x ( ) ( ) + w 2 f 2 x ( ) y y 15

Ordinary Least Squares (OLS) 2 # & 2  ( ) ( ) total error = ∑ y i − y ∑ y i − ∑ w k f k x = % ( i $ ' i i k 16

Minimizing Error Imagine we had only one point x with features f(x): 2 1 ⎛ ⎞ error w y w f x ( ) ( ) ∑ = − ⎜ ⎟ k k 2 ⎝ ⎠ k error w ( ) ∂ ⎛ ⎞ y w f x f x ( ) ( ) ∑ = − − ⎜ ⎟ k k m w ∂ ⎝ ⎠ k m ⎛ ⎞ w w y w f x f x ( ) ( ) ∑ ← + α − ⎜ ⎟ m m k k m ⎝ ⎠ k Approximate q update as a one-step gradient descent : “target” “prediction” ⎡ ⎤ w w r max Q s ( ', ') a Q ( , ) s a f x ( ) ← + α + γ − m m m ⎣ ⎦ a 17

How many features should we use? Ø As many as possible? • computational burden • overfitting Ø Feature selection is important • requires domain expertise 18

Overfitting 19

Overview of Project 3 Ø MDPs • Q1: value iteration • Q2: find parameters that lead to certain optimal policy • Q3: similar to Q2 Ø Q-learning • Q4: implement the Q-learning algorithm • Q5: implement ε greedy action selection • Q6: try the algorithm Ø Approximate Q-learning and state abstraction • Q7: Pacman Ø Tips • make your implementation general 20