Random Walks in Graphs Thomas Bonald Stage LIESSE 2018
Schedule ◮ 9:30 - 12:30 Tutorial ◮ 12:30 - 13:30 Lunch ◮ 13:30 - 17:00 Lab session (python)
Graph data ◮ Infrastructure: roads, railways, power grid, internet, ... Main European highways
Graph data ◮ Infrastructure: roads, railways, power grid, internet, ... ◮ Communication: phone, emails, flights, ... International flights
Graph data ◮ Infrastructure: roads, railways, power grid, internet, ... ◮ Communication: phone, emails, flights, ... ◮ Information: Web, Wikipedia, knowledge bases, ... David Hilbert Mathematical analysis René Descartes Euclid Euclidean geometry Mathematics Pythagorean theorem Calculus Geometry Topology Symmetry Physics String theory Extract from Wikipedia
Graph data ◮ Infrastructure: roads, railways, power grid, internet, ... ◮ Communication: phone, emails, flights, ... ◮ Information: Web, Wikipedia, knowledge bases, ... Carmen Maura Blanca Portillo Yohana Cobo Lola Dueñas Chus Lampreave Volver Murder on the Orient Express (2017 film) Vanilla Sky Twice Born Don't Move Gothika Grimsby (film) Vicky Cristina Barcelona The Greek Labyrinth Manolete (film) Sahara (2005 film) Love Can Seriously Damage Your Health For Love, Only for Love Woman on Top Captain Corelli's Mandolin (film) The Good Night Chromophobia (film) Head in the Clouds Elegy (film) The Girl of Your Dreams American Crime Story Penélope Cruz Entre rojas Don't Tempt Me The Counselor Belle Époque (film) Volavérunt Jamón Jamón Ma Ma (2015 film) To Rome with Love (film) Broken Embraces Blow (film) All the Pretty Horses (film) Noel (film) The Hi-Lo Country Alegre ma non troppo La Celestina (1996 film) Todo es mentira Open Your Eyes (1997 film) The Rebel (1993 film) The Man with Rain in His Shoes Zoolander 2 Bandidas G-Force (film) Nine (2009 live-action film) All About My Mother Extract from the movie-actor graph
Graph data ◮ Infrastructure: roads, railways, power grid, internet, ... ◮ Communication: phone, emails, flights, ... ◮ Information: Web, Wikipedia, knowledge bases, ... ◮ Social networks: Facebook, Twitter, LinkedIn, ... Extract from Twitter Source: AllThingsGraphed.com
Graph data ◮ Infrastructure: roads, railways, power grid, internet, ... ◮ Communication: phone, emails, flights, ... ◮ Information: Web, Wikipedia, knowledge bases, ... ◮ Social networks: Facebook, Twitter, LinkedIn, ... ◮ Biology: brain, proteins, phylogenetics, ... The brain network Source: Wired
Graph data ◮ Infrastructure: roads, railways, power grid, internet, ... ◮ Communication: phone, emails, flights, ... ◮ Information: Web, Wikipedia, knowledge bases, ... ◮ Social networks: Facebook, Twitter, LinkedIn, ... ◮ Biology: brain, proteins, phylogenetics, ... ◮ Health: genetic diseases, patient-doctor-pharmacy-drugs, ... Pharmacy-doctor network Source: IAAI 2015
Graph data ◮ Infrastructure: roads, railways, power grid, internet, ... ◮ Communication: phone, emails, flights, ... ◮ Information: Web, Wikipedia, knowledge bases, ... ◮ Social networks: Facebook, Twitter, LinkedIn, ... ◮ Biology: brain, proteins, phylogenetics, ... ◮ Health: genetic diseases, patient-doctor-pharmacy-drugs, ... ◮ Marketing: customer-product, bundling, ...
Data as graph ◮ Dataset x 1 , . . . , x n ∈ X ◮ Similarity measure σ : X × X → R + ◮ Graph of n nodes with weight σ ( x i , x j ) between nodes i and j 1.0 0.8 0.6 0.4 0.2 0.0 0.0 0.2 0.4 0.6 0.8 1.0 Example: X = [0 , 1] 2 , σ ( x , y ) = 1 { d ( x , y ) < 1 / 4 }
Data as graph ◮ Dataset x 1 , . . . , x n ∈ X ◮ Similarity measure σ : X × X → R + ◮ Graph of n nodes with weight σ ( x i , x j ) between nodes i and j Example: X = [0 , 1] 2 , σ ( x , y ) = 1 { d ( x , y ) < 1 / 4 }
Motivation ◮ Information retrieval ◮ Content recommandation ◮ Advertizing ◮ Anomaly detection ◮ Security
Graph analysis ◮ What are the most important nodes? → Ranking ◮ Can we predict new links? → Local ranking ◮ What is the graph structure? → Clustering ◮ Can we predict labels? → Classification
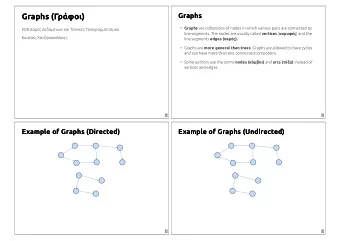
Setting A weighted, undirected, connected graph of n nodes No self-loops Weighted adjacency matrix A Vector of node weights d = A 1
Outline 1. Random walk 2. Laplacian matrix 3. Spectral analysis 4. Graph embedding 5. Applications
Outline 1. Random walk → Statistical physics 2. Laplacian matrix → Heat equation 3. Spectral analysis → Mechanics 4. Graph embedding → Electricity 5. Applications
Outline 1. Random walk → Statistical physics 2. Laplacian matrix → Heat equation 3. Spectral analysis → Mechanics 4. Graph embedding → Electricity 5. Applications
Random walk Consider a random walk in the graph G where the probability of moving from node i to node j is A ij / d i
Random walk Consider a random walk in the graph G where the probability of moving from node i to node j is A ij / d i The sequence of nodes X 0 , X 1 , X 2 , . . . defines a Markov chain on { 1 , . . . , n } with transition matrix P = D − 1 A
Random walk Consider a random walk in the graph G where the probability of moving from node i to node j is A ij / d i The sequence of nodes X 0 , X 1 , X 2 , . . . defines a Markov chain on { 1 , . . . , n } with transition matrix P = D − 1 A ◮ Dynamics: � P ( X t +1 = i ) = P ( X t = j ) P ji j
Random walk Consider a random walk in the graph G where the probability of moving from node i to node j is A ij / d i The sequence of nodes X 0 , X 1 , X 2 , . . . defines a Markov chain on { 1 , . . . , n } with transition matrix P = D − 1 A ◮ Dynamics: � P ( X t +1 = i ) = P ( X t = j ) P ji j ◮ Stationary distribution π : � � P ( X ∞ = i ) = P ( X ∞ = j ) P ji ⇐ ⇒ π i = π j P ji j j (global balance)
Return time Since π i is the frequency of visits of node i in stationary regime, the mean return time to node i is given by i ) = 1 σ i = E i ( τ + π i with τ + = min { t ≥ 1 : X t = i } i
Reversibility A Markov chain is called reversible if in stationary regime, the probability of any sequence of states is the same in both directions of time
Reversibility A Markov chain is called reversible if in stationary regime, the probability of any sequence of states is the same in both directions of time ◮ Transition from state i to state j : P ( X t = i , X t +1 = j ) = P ( X t = j , X t +1 = i ) ⇐ ⇒ π i P ij = π j P ji (local balance)
Reversibility A Markov chain is called reversible if in stationary regime, the probability of any sequence of states is the same in both directions of time ◮ Transition from state i to state j : P ( X t = i , X t +1 = j ) = P ( X t = j , X t +1 = i ) ⇐ ⇒ π i P ij = π j P ji (local balance) ◮ Sequence of states i 0 , i 1 , . . . i ℓ : P ( X t = i 0 , . . . , X t + ℓ = i ℓ ) = P ( X t = i ℓ , . . . , X t + ℓ = i 0 ) ⇐ ⇒ π i 0 P i 0 i 1 . . . P i ℓ − 1 i ℓ = π i ℓ P i ℓ i ℓ − 1 . . . P i 1 i 0
Reversibility & random walks ◮ The random walk in a graph is a reversible Markov chain, with stationary distribution π ∝ d
Reversibility & random walks ◮ The random walk in a graph is a reversible Markov chain, with stationary distribution π ∝ d ◮ Conversely, any reversible Markov chain is a random walk in a graph, with weights π i P ij = π j P ji
Reversibility in physics ◮ All microscopic laws of physics are reversible
Reversibility in physics ◮ All microscopic laws of physics are reversible ◮ The second law of thermodynamics states that the evolution of any isolated system is irreversible
Reversibility in physics ◮ All microscopic laws of physics are reversible ◮ The second law of thermodynamics states that the evolution of any isolated system is irreversible ◮ This apparent paradox was solved by Tatiana & Paul Ehrenfest in 1907
Example
Hitting time, commute time & escape probability ◮ Mean hitting time of node j from node i : H ij = E i ( τ j ) , τ j = min { t ≥ 0 : X t = j } ◮ Mean commute time between nodes i and j : ρ ij = H ij + H ji ◮ Escape probability from node i to node j : e ij = P i ( τ j < τ + i ) Proposition 1 ρ ij = π i e ij
Proof
Frequency of no-return paths ∀ i � = j π i e ij = π j e ji
Outline 1. Random walk → Statistical physics 2. Laplacian matrix → Heat equation 3. Spectral analysis → Mechanics 4. Graph embedding → Electricity 5. Applications
Laplacian matrix Let D = diag ( A 1). Definition The matrix L = D − A is called the Laplacian matrix . Heat equation ◮ Fix the temperature of some nodes S ⊂ { 1 , . . . , n } ◮ Interpret the weight A ij as the thermal conductivity ◮ Then for any node i �∈ S , dT � dt = A ij ( T j − T i ) = − ( LT ) i j
Example
Example
Example
Equilibrium Dirichlet problem ◮ For any node i �∈ S , ( LT ) i = 0 with boundary condition T i for all i ∈ S ◮ The vector T is said to be harmonic Uniqueness There is at most one solution to the Dirichlet problem Proof based on the maximum principle
The maximum principle
Recommend
More recommend
