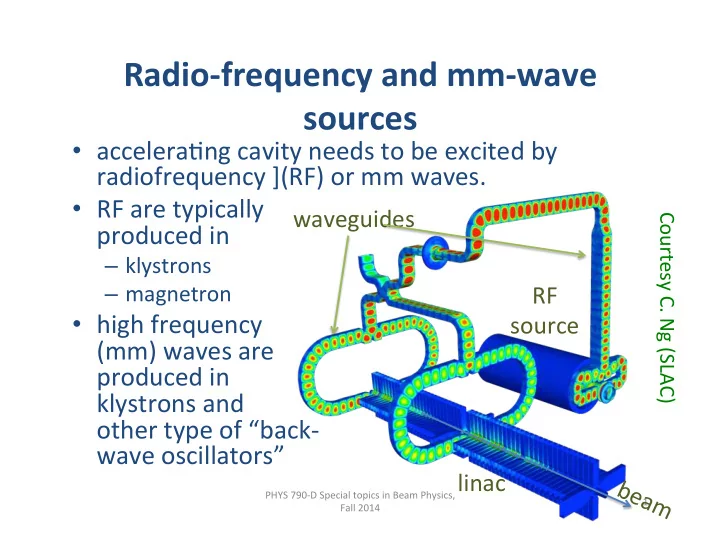
Radio-frequency and mm-wave sources accelera&ng cavity - PowerPoint PPT Presentation

Radio-­‑frequency ¡and ¡mm-­‑wave ¡ sources ¡ • accelera&ng ¡cavity ¡needs ¡to ¡be ¡excited ¡by ¡ ¡ radiofrequency ¡](RF) ¡or ¡mm ¡waves. ¡ • RF ¡are ¡typically ¡ ¡ waveguides ¡ Courtesy ¡C. ¡Ng ¡(SLAC) ¡ produced ¡in ¡ ¡ – klystrons ¡ – magnetron ¡ RF ¡ • high ¡frequency ¡ source ¡ (mm) ¡waves ¡are ¡ ¡ produced ¡in ¡ ¡ klystrons ¡and ¡ ¡ other ¡type ¡of ¡“back-­‑ ¡ wave ¡oscillators” ¡ ¡ linac ¡ PHYS ¡790-­‑D ¡Special ¡topics ¡in ¡Beam ¡Physics, ¡ 1 ¡ Fall ¡2014 ¡

Principle ¡of ¡an ¡RF ¡source ¡ • transform ¡a ¡dc ¡electron ¡beam ¡into ¡a ¡train ¡of ¡ bunches ¡ • use ¡this ¡train ¡to ¡excite ¡a ¡radia&ve ¡process ¡ Appl. ¡Phys. ¡LeU. ¡98, ¡261501 ¡(2011) ¡ • emiUed ¡radia&on ¡ ¡ Bunch ¡form ¡factor ¡ ¡ is ¡coherently ¡ ¡ enhanced ¡at ¡ ¡ the ¡bunching ¡ ¡ frequency ¡ ¡ (see ¡HW3) ¡ PHYS ¡790-­‑D ¡Special ¡topics ¡in ¡Beam ¡Physics, ¡ 2 ¡ Fall ¡2014 ¡

RF ¡source ¡– ¡historical ¡context ¡ • method ¡to ¡produce ¡e-­‑ ¡beam ¡with ¡“varying ¡density” ¡ conceived ¡by ¡D. ¡Rozhansky ¡from ¡Leningrad ¡Polytechnic ¡ Ins&tute ¡(1935) ¡ • UK ¡patent ¡by ¡O. ¡Heil ¡(1935) ¡ • theory ¡of ¡velocity ¡modula&on ¡ ¡ and ¡beam ¡bunching ¡by ¡ ¡ A. ¡Arsenjewa-­‑Heil, ¡and ¡ ¡ O. ¡Heil, ¡Z. ¡f. ¡Physik ¡95 ¡(1935) ¡ • Varian ¡brothers ¡build ¡a ¡ ¡ klystron ¡(1937) ¡ • Hansen ¡(SLAC) ¡invents ¡the ¡first ¡ ¡ cavity ¡ ¡ PHYS ¡790-­‑D ¡Special ¡topics ¡in ¡Beam ¡Physics, ¡ 3 ¡ Fall ¡2014 ¡

A ¡simple ¡klystron ¡configura@on ¡ • (see ¡HW3) ¡ PHYS ¡790-­‑D ¡Special ¡topics ¡in ¡Beam ¡Physics, ¡ 4 ¡ Fall ¡2014 ¡

Principle ¡of ¡opera@on ¡ • c ¡ PHYS ¡790-­‑D ¡Special ¡topics ¡in ¡Beam ¡Physics, ¡ 5 ¡ Fall ¡2014 ¡

Example ¡of ¡klystrons ¡ • . ¡ PHYS ¡790-­‑D ¡Special ¡topics ¡in ¡Beam ¡Physics, ¡ 6 ¡ Fall ¡2014 ¡

Simple ¡theory ¡ • 1 st ¡stage: ¡produc&on ¡of ¡a ¡dc ¡electron ¡beam ¡ – the ¡beam ¡kine&c ¡energy ¡is ¡given ¡by ¡the ¡applied ¡DC ¡ voltage: ¡ 1 2 mu 2 0 = eV 0 • 2 nd ¡stage ¡is ¡to ¡apply ¡a ¡&me-­‑dependent ¡voltage ¡ ¡ on ¡the ¡bunch ¡ ¡ PHYS ¡790-­‑D ¡Special ¡topics ¡in ¡Beam ¡Physics, ¡ 7 ¡ Fall ¡2014 ¡

Simple ¡theory: ¡electron ¡emission ¡ – the ¡change ¡in ¡kine&c ¡energy ¡is ¡therefore ¡ ¡ 1 2 mu 2 − 1 2 mu 2 0 = eV 1 sin ω t • the ¡final ¡velocity ¡is ¡ ¡ ¡ r 1 + eV 1 u ( t ) = u 0 sin ω t V 0 PHYS ¡790-­‑D ¡Special ¡topics ¡in ¡Beam ¡Physics, ¡ 8 ¡ Fall ¡2014 ¡

@me ¡of ¡arrival ¡at ¡“output ¡gap” ¡ • assume ¡ ¡ ¡ ¡ V 1 /V 0 ⌧ 1 • consider ¡an ¡electron ¡that ¡get ¡an ¡ “instantaneous” ¡velocity ¡modula&on ¡at ¡ t 1 • ¡if ¡ ¡ ¡ ¡is ¡the ¡separa&on ¡between ¡the ¡two ¡“gaps” ¡ l the ¡the ¡&me ¡of ¡arrival ¡at ¡the ¡2 nd ¡gap ¡is ¡ ¡ t 2 = t 1 + l u ' t 1 + l lV 1 sin ω t 1 � u 0 2 u 0 V 0 PHYS ¡790-­‑D ¡Special ¡topics ¡in ¡Beam ¡Physics, ¡ 9 ¡ Fall ¡2014 ¡

Final ¡current ¡ • introducing ¡a ¡phase ¡ ¡ ϕ ≡ ω t • the ¡laUer ¡equa&on ¡rewrites ¡ ¡ ω t 2 = ω t 1 + θ 0 − X sin ω t 1 • the ¡charge ¡conserva&on ¡requires ¡ ¡ I 1 dt 1 = I 2 dt 2 • but ¡ ¡ dt 2 = 1 + X cos ω t 1 dt 1 PHYS ¡790-­‑D ¡Special ¡topics ¡in ¡Beam ¡Physics, ¡ 10 ¡ Fall ¡2014 ¡

Final ¡current ¡ • so ¡that ¡the ¡final ¡current ¡can ¡be ¡wriUen ¡ I 1 I 2 = 1 − X cos ω t 1 • current ¡can ¡in ¡principle ¡be ¡infinite ¡ • we ¡can ¡relate ¡this ¡with ¡our ¡1 st ¡order ¡beam ¡ dynamics ¡approach ¡(introducing ¡the ¡R56 ¡of ¡a ¡ drie ¡space… ¡) ¡ ¡ PHYS ¡790-­‑D ¡Special ¡topics ¡in ¡Beam ¡Physics, ¡ 11 ¡ Fall ¡2014 ¡

final ¡current ¡ • the ¡final ¡current ¡is ¡limited ¡by ¡field ¡ nonlineari&es ¡and ¡space ¡charge ¡effects ¡ PHYS ¡790-­‑D ¡Special ¡topics ¡in ¡Beam ¡Physics, ¡ 12 ¡ Fall ¡2014 ¡

final ¡current ¡ • In ¡prac&ce ¡the ¡final ¡current ¡is ¡wriUen ¡as ¡the ¡ Fourier ¡series: ¡ ∞ ¡ X I 2 = I 1 + a n cos n ( ω t 2 − θ 0 ) 1 • where ¡ Z θ 0 + π a n = 1 cos[ n ( ω t 2 − θ 0 )] d ( ω t 2 ) π θ 0 − π Z π = I 1 cos[ n ( ω t 1 − X sin( ω t 1 )] d ( ω t 1 ) π − π = 2 I 1 J n ( nX ) PHYS ¡790-­‑D ¡Special ¡topics ¡in ¡Beam ¡Physics, ¡ 13 ¡ Fall ¡2014 ¡

efficiency ¡(at ¡fundamental ¡ f ) ¡ max[ I ] = 2 × 0 . 58 • maximum ¡current ¡is ¡ • for ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡so ¡that ¡output ¡power ¡at ¡the ¡ ¡ X = 1 . 84 fundamental ¡frequency ¡(n=1) ¡is ¡ ¡ P out = 1 . 16 I 1 V 0 2 = 0 . 58 P in √ √ 2 • ~60% ¡efficiency ¡conver&ng ¡DC ¡power ¡into ¡the ¡ fundamental ¡harmonic ¡ ¡ • addi&onal ¡contribu&on ¡comes ¡from ¡the ¡output ¡ coupling ¡(power ¡extrac&on ¡from ¡the ¡cavity) ¡ PHYS ¡790-­‑D ¡Special ¡topics ¡in ¡Beam ¡Physics, ¡ 14 ¡ Fall ¡2014 ¡

other ¡source ¡magnetron ¡ • cheaper ¡and ¡more ¡compact ¡than ¡klystrons ¡but ¡ harder ¡to ¡stabilize ¡ cathode ¡ anode ¡block ¡ resonant ¡cavi&es ¡ coaxial ¡coupler ¡ (power ¡extrac&on) ¡ interac&on ¡ space ¡ PHYS ¡790-­‑D ¡Special ¡topics ¡in ¡Beam ¡Physics, ¡ 15 ¡ Fall ¡2014 ¡

magnetron ¡opera@on ¡ • velocity ¡and ¡density ¡bunching ¡happens ¡axially ¡ hUp://www.radartutorial.eu/08.transmiUers/ Magnetron.en.html ¡ PHYS ¡790-­‑D ¡Special ¡topics ¡in ¡Beam ¡Physics, ¡ 16 ¡ Fall ¡2014 ¡

backward ¡wave ¡oscillators ¡ • slow ¡wave ¡structure ¡ ¡ used ¡to ¡bunch ¡the ¡ ¡ beam ¡ • an ¡evanescent ¡ ¡ back-­‑propaga&ng ¡ ¡ wave ¡(nega&ve ¡ ¡ group ¡velocity ¡ ¡ interacts ¡with ¡the ¡ ¡ dc ¡beam ¡to ¡produce ¡ ¡ a ¡bunch ¡train) ¡ PHYS ¡790-­‑D ¡Special ¡topics ¡in ¡Beam ¡Physics, ¡ 17 ¡ Fall ¡2014 ¡