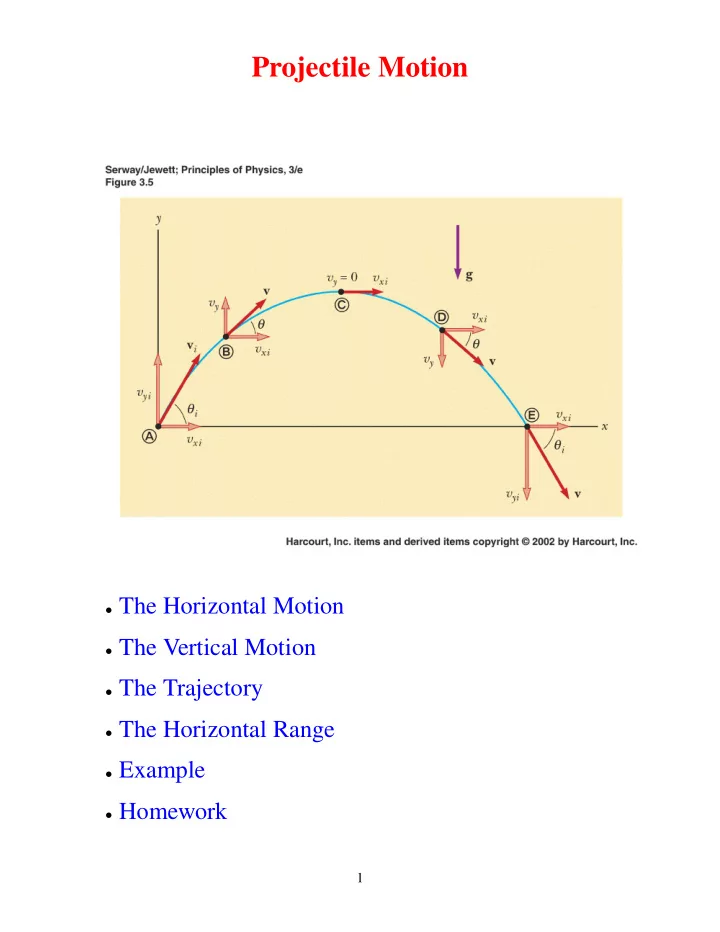
Projectile Motion The Horizontal Motion The Vertical Motion The - PDF document

Projectile Motion • The Horizontal Motion • The Vertical Motion • The Trajectory • The Horizontal Range • Example • Homework 1

The Horizontal Motion a x = 0 v xf = v xi = v i cos θ i = constant ⇒ x f = x i + v xi t = x i + ( v i cos θ i ) t (1) 2

The Vertical Motion a y = − g y f = y i + v yi t − 1 2 gt 2 = y i + ( v i sin θ i ) t − 1 2 gt 2 (2) v yf = v yi − gt = v i sin θ i − gt (3) yi − 2 g ( y f − y i ) = ( v i sin θ i ) 2 − 2 g ( y f − y i ) (4) v 2 yf = v 2 3

The Trajectory • Solving eqn. (1) for t we have t = x f − x i v i cos θ i • Substituting this into eqn. (2) and setting x i = y i = 0 , we get x f  − 1 x f 2     y f = ( v i sin θ i ) 2 g        v i cos θ i v i cos θ i  g   x 2 y f = (tan θ i ) x f − (5)     f 2 ( v i cos θ i ) 2  • Eqn. (5) has the form y = ax + bx 2 where a and b are constants ⇒ the trajectory of a projectile is parabolic 4

The Horizontal Range x f − x i = R y f − y i = 0 Eqn. (1) R = ( v i cos θ i ) t ⇒ 0 = ( v i sin θ i ) t − 1 2 gt 2 Eqn. (2) ⇒ t = 2 v i sin θ i g 5

The Horizontal Range (cont’d) R = 2 v 2 i g sin θ i cos θ i sin 2 θ i = 2 sin θ i cos θ i R = v 2 i g sin 2 θ i Note: R is a maximum when sin 2 θ i = 1 ⇒ 2 θ i = 90 ◦ or θ i = 45 ◦ 6

Example A soccer player kicks a ball at an angle of 38 ◦ from the horizontal, with an initial speed of 15 m/s. (a) How long is the ball in the air? (b) How far down the field does the ball land? (c) How high does the ball go? 7

Example Solution A soccer player kicks a ball at an angle of 38 ◦ from the horizontal, with an initial speed of 15 m/s. (a) How long is the ball in the air? v i = 15 m/s θ i = 38 ◦ y f = y i y f − y i = ( v i sin θ i ) t − 1 2 gt 2 = 0 t = 2 v i sin θ i = 2 (15 m/s ) sin 38 ◦ = 1 . 9 s g 9 . 8 m/s 2 (b) How far down the field does the ball land? x f − x i = ( v i cos θ i ) t = (15 m/s ) (cos 38 ◦ ) (1 . 9 s ) = 22 m (c) How high does the ball go? v yf = 0 yf = ( v i sin θ i ) 2 − 2 g ( y f − y i ) = 0 v 2 i sin 2 θ i = (15 m/s ) sin 2 38 ◦ y f − y i = v 2 = 4 . 4 m 2 g 2 (9 . 8 m/s 2 ) 8

Homework Set 7 - Due Fri. Sept. 24 • Read Section 3.3 • Do Problems 3.9, 3.11 & 3.14 9