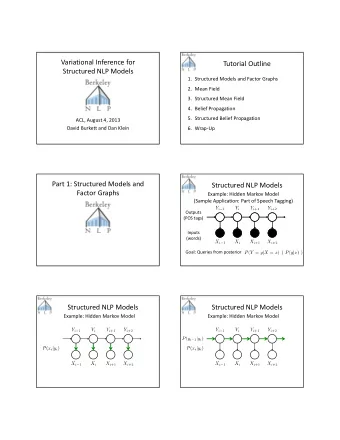
PROBABILISTIC MODELS FOR STRUCTURED DATA 1: Introduction Instructor: Yizhou Sun yzsun@cs.ucla.edu January 6, 2020
Instructor • Yizhou Sun • yzsun@cs.ucla.edu • http://web.cs.ucla.edu/~yzsun/ • Research areas • graph mining, social/information network mining, text mining, web mining • Data mining, machine learning 2
Logistics of the Course • Grading • Participation: 5% • Homework: 30% • Paper presentation: 25% • Group-based • Course project: 40% • Group-based 3
Lectures • Part I: Lectures by the instructor (5 weeks) • Cover the basic materials • Part II: paper presentation by students (4 weeks) • Extended materials, which require in-depth reading of papers • Part III: course project presentation (Week 10) 4
Homework • Weekly quick homework in Part I • A quiz style homework for each paper, due every lecture in Part II • The paper presenters are in charge of homework question, solution, and discussion, which is expected to finish in class 5
Paper Presentation • What to present • Each student sign-up for one group of research papers • Every group can be signed by at 3-4 students • How long for each presentation? • 1 lecture, including Q&A, homework time, and homework discussion • When to present • From Week 6 to Week 9 • How to present • Make slides, when necessary, using blackboard • What else? • Design a in-class homework with 1-2 well designed questions • Send the slides and homework (with correct answer) to me the day before the lecture • Provide the discussion to the solution in class 6
Course Project • Research project • Goal: design a probabilistic graphical model to solve the candidate problems or problems of your own choice, and write a report that is potentially submitted to some venue for publication • Teamwork • 3-4 people per group • Timeline • Team formation due date: Week 2 • Proposal due date: Week 5 • Presentation due date: 3/12/2019 (10-12pm) • Final report due date: 3/13/2019 • What to submit: project report and code 7
Content • What are probabilistic models • What are structured data • Applications • Key tasks and challenges 8
A Typical Machine Learning Problem • Given a feature vector x , predict its label y (discrete or continuous) 𝑧 = 𝑔 𝒚 • Example: Text classification • Given a news article, which category does it belong to? Argentina played to a frustrating 1-1 ties against Sports ? Iceland on Saturday. A stubborn Icelandic defense Politics was increasingly tough to penetrate, and a Lionel Education MESSI missed penalty was a huge turning point in … the match, because it likely would’ve given Argentina three points. 9
Probabilistic Models 𝑜 • Data: 𝐸 = 𝒚 𝑗 , 𝑧 𝑗 𝑗=1 • n: number of data points • Model: 𝑞 𝐸 𝜄 𝑝𝑠 𝑞 𝜄 (𝐸) • Use probability distribution to address uncertainty • 𝜄 : parameters in the model • Inference: ask questions about the model • Marginal inference: marginal probability of a variable • Maximum a posteriori (MAP) inference: most likely assignment of variables • Learning: learn the best parameters 𝜄 10
The I.I.D. Assumption • Assume data points are independent and identically distributed (i.i.d.) • 𝑞 𝐸|𝜄 = ς 𝑗 𝑞(𝒚 𝑗 , 𝑧 𝑗 |𝜄) (if modeling joint distribution) • 𝑞 𝐸|𝜄 = ς 𝑗 𝑞(𝑧 𝑗 |𝒚 𝑗 , 𝜄) (if modeling conditional distribution, conditional i.i.d.) • Example: linear regression 𝑈 𝜸, 𝜏 2 ) • 𝑧 𝑗 |𝒚 𝑗 , 𝜸~𝑂(𝒚 𝑗 𝑈 𝜸 + ε 𝑗 , where ε 𝑗 ~𝑂 0, 𝜏 2 • 𝑧 𝑗 = 𝒚 𝑗 2 𝑈 𝜸 2𝜌𝜏 2 exp{− 𝑧 𝑗 − 𝒚 𝑗 1 𝑞 𝐸 𝜸 = ෑ 𝑞 𝑧 𝑗 𝒚 𝑗 , 𝜸) = ෑ } 2𝜏 2 𝑗 𝑗 𝑀 𝜸 : 𝑚𝑗𝑙𝑓𝑚𝑗ℎ𝑝𝑝𝑒 𝑔𝑣𝑜𝑑𝑢𝑗𝑝𝑜 11
Content • What are probabilistic models • What are structured data • Applications • Key tasks and challenges 12
Structured Data • Dependency between data points • Dependency are described by links • Example: paper citation network • Citation between papers introduces dependency 13
Examples of Structured Data • Text The cat sat on the mat • sequence • Image • Grid / regular graph • Social/Information Network • General graph 14
Roles of Data Dependency • I.I.D. or conditional I.I.D. assumption no longer holds • 𝑞 𝐸|𝜄 ≠ ς 𝑗 𝑞 𝒚 𝑗 , 𝑧 𝑗 𝜄 , or • 𝑞 𝐸|𝜄 ≠ ς 𝑗 𝑞 𝑧 𝑗 𝒚 𝑗 , 𝜄 • Example • In paper citation network, a paper is more likely to share the same label (research area) of its references Paper i’s label Paper j’s label Probability Suppose i cites j 0 0 0.4 or j cites i 0 1 0.1 1 0 0.1 1 1 0.4 15
Scope of This Course • A subset of probabilistic graphical model • Consider data dependency • Markov Random Fields, Conditional Random Fields, Factor Graph, and their applications in text, image, knowledge graph, and social/information networks • Recent development of integrating deep learning and graphical models • A full cover of probabilistic graphical models can be found: • Stanford course • Stefano Ermon, CS 228: Probabilistic Graphical Models • Daphne Koller, Probabilistic Graphical Models, YouTube • CMU course • Eric Xing, 10-708: Probabilistic Graphical Models 16
Content • What are probabilistic models • What are structured data • Applications • Key tasks and challenges 17
Text NER • Named-Entity Recognition • Given a predefined label set, determine each word’s label • E.g., B-PER, I-PER, O • Possible solution: Conditional random field • https://nlp.stanford.edu/software/CRF-NER.html 18
Image Semantic Labeling • Determine the label of each pixel • Given a predefined label set, determine each pixel’s label • Possible solution: Conditional random field 19
Social Network Node Classification • Attribute prediction of Facebook users • E.g., gender • Zheleva et al., Higher-order Graphical Models for Classification in Social and Affiliation Networks, NIPS’2010 20
Content • What are probabilistic models • What are structured data • Applications • Key tasks and challenges 21
Key Tasks • Model • From data model to graphical model • Define joint probability of all the data according to graphical model • 𝑞 𝐸 𝜄 𝑝𝑠 𝑞 𝜄 (𝐸) • Inference • Marginal inference: marginal probability of a variable • Maximum a posteriori (MAP) inference: most likely assignment of variables • Learning • Learn the best parameters 𝜄 22
Key Challenges • Design challenges in modeling • How to use heuristics to design meaningful graphical model? • Computational challenges in inference and learning • Usually are NP-hard problems • Need approximate algorithms 23
Course Overview • Preliminary • Introduction • Basic probabilistic models • Naïve Bayes • Logistic Regression • Warm up: Hidden Markov Models • Forward Algorithm, Viterbi Algorithm, The Forward-Backward Algorithm • Markov Random Fields • General MRF, Pairwise MRF • Variable elimination, sum-product message passing, max-product message passing, exponential family, pseudo-likelihood • Conditional Random Fields • General CRF, Linear Chain CRF • Factor Graph 24
Probability Review • Follow Stanford CS229 Probability Notes • http://cs229.stanford.edu/section/cs229- prob.pdf 25
Major Concepts • Elements of Probability • Sample space, event space, probability measure • Conditional probability • Independence, conditional independence • Random variables • Cumulative distribution function, Probability mass function (for discrete random variable), Probability density function (for continuous random variable) • Expectation, variance • Some frequently used distributions • Discrete: Bernoulli, binomial, geometric, Poisson • Continuous: uniform, exponential, normal • More random variables • Joint distribution, marginal distribution, joint and marginal probability mass function, joint and marginal density function • Chain rule • Bayes’ rule • Independence • Expectation, conditional expectation, and covariance 26
Summary • What are probabilistic models • Model uncertainty • What are structured data • Use links to capture dependency between data • Applications • Text, image, social/information network • Key tasks and challenges • Modeling, inference, learning 27
References • Daphne Koller and Nir Friedman (2009). Probabilistic Graphical Models. The MIT Press. • Kevin P. Murphy (2012). Machine Learning: A Probabilistic Perspective. The MIT Press. • Charles Sutton and Andrew McCallum (2014). An Introduction to Conditional Random Fields. Now Publishers. • Zheleva et al., Higher-order Graphical Models for Classification in Social and Affiliation Networks, NIPS’2010 • https://cs.stanford.edu/~ermon/cs228/index.html • https://nlp.stanford.edu/software/CRF-NER.html • http://cs229.stanford.edu/section/cs229-prob.pdf 28
Recommend
More recommend
