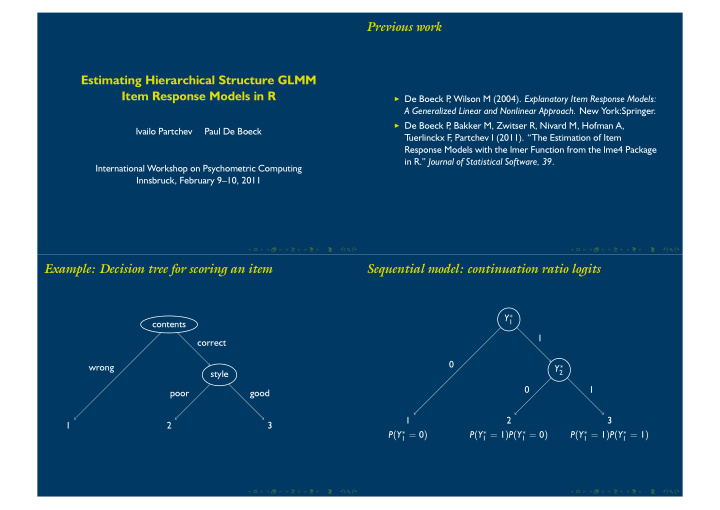
Previous work Estimating Hierarchical Structure GLMM Item Response - PowerPoint PPT Presentation

Previous work Estimating Hierarchical Structure GLMM Item Response Models in R ◮ De Boeck P , Wilson M (2004). Explanatory Item Response Models: A Generalized Linear and Nonlinear Approach. New York:Springer. ◮ De Boeck P , Bakker M, Zwitser R, Nivard M, Hofman A, Ivailo Partchev Paul De Boeck T uerlinckx F , Partchev I (2011). “The Estimation of Item Response Models with the lmer Function from the lme4 Package in R.” Journal of Statistical Software, 39 . International Workshop on Psychometric Computing Innsbruck, February 9–10, 2011 Example: Decision tree for scoring an item Sequential model: continuation ratio logits Y ∗ 1 contents 1 correct 0 wrong Y ∗ 2 style 0 1 poor good 1 2 3 1 2 3 P ( Y ∗ 1 = 0 ) P ( Y ∗ 1 = 1 ) P ( Y ∗ 1 = 0 ) P ( Y ∗ 1 = 1 ) P ( Y ∗ 1 = 1 )

Partial credit model: adjacent logits Graded response model: cumulative logits contents R 1 exp ( θ 1 + β 1 ) correct exp ( 0 ) wrong style R 2 exp ( 0 ) exp ( θ 2 + β 2 ) poor good 1 2 3 1 2 3 exp ( 0 ) exp ( 0 ) exp ( θ 1 + β 1 ) exp ( θ 1 + β 1 ) exp ( θ 2 + β 2 ) 1 − R 1 R 1 − R 2 R 2 Another example: Slow and fast intelligence Research issue θ 1 + β 1 Does the intelligence involved in fast correct responses differ in nature from the intelligence involved in slow correct responses with slow fast respect to: ◮ the processes involved? θ 2 + β 2 θ 3 + β 3 ◮ the abilities involved? wrong wrong correct correct Or, more simply, ◮ Is fast intelligence the same as slow intelligence: θ 2 = θ 3 ? 1 2 3 4 ◮ Is fast difficulty the same as slow difficulty: β 2 = β 3 ? 1 → 00 • 2 → 01 • 3 → 1 • 0 4 → 1 • 1

Material Analyses with ConQuest ◮ Fixed effects for items, random effects for persons ◮ A verbal analogies test (Hornke & Rettig, 1993): proportions of ◮ Full model 3I–3P compared with constrained models 2I–3P , success from 0.026 to 0.985, mean response time 18 s (SD 3I–2P , and 2I–2P 15.7); relibility of fast responses 0.746 (within-person split), ◮ Full model fit satisfactory; relative fit of constrained models 0.701 (within-item split); relibility of slow responses 0.705 significantly worse (within-person split), 0.643 (within-item split), for a subset of 726 persons and 34 items ◮ A Raven-type matrices test (Hornke & Habon, 1986): proportions of success from 0.102 to 0.772, mean response time 69 s (SD 51.5); relibility of fast responses 0.727 (within-person split), 0.768 (within-item split); relibility of slow responses 0.679 (within-person split), 0.630 (within-item split), for a subset of 503 persons and 35 items Analyses with ConQuest Analyses with ConQuest ◮ Fixed effects for items, random effects for persons ◮ Fixed effects for items, random effects for persons ◮ Full model 3I–3P compared with constrained models 2I–3P ◮ Full model 3I–3P compared with constrained models 2I–3P , , 3I–2P , and 2I–2P 3I–2P , and 2I–2P ◮ Full model fit satisfactory; relative fit of constrained models ◮ Full model fit satisfactory; relative fit of constrained models significantly worse significantly worse ◮ Correlations between the two accuracy abilities high but not ◮ Correlations between the two accuracy abilities high but not perfect: 0.873 and 0.879 for verbal analogies and 0.880 and perfect: 0.873 and 0.879 for verbal analogies and 0.880 and 0.869 for matrices, for the split within persons and within items, 0.869 for matrices, for the split within persons and within items, respectively respectively ◮ Estimated variances larger for fast than for slow ◮ verbal analogies: 1.19 (slow) 2.77 (fast) with a split within persons, 1.22 (slow) 2.02 (fast) with a split within items ◮ verbal analogies: 0.85 (slow) 1.71 (fast) with a split within persons, 1.02 (slow) 1.59 (fast) with a split within items

Analyses with glmer Analyses with glmer ◮ Determine whether the difference in fit is due primarily to the ◮ Determine whether the difference in fit is due primarily to the imperfect correlation or to the difference in reliability imperfect correlation or to the difference in reliability ◮ Random parameters for both persons and items ◮ Random parameters for both persons and items ◮ Reparameterization of slow and fast accuracy as a general ◮ Reparameterization of slow and fast accuracy as a general accuracy and a specific variable for fast accuracy accuracy and a specific variable for fast accuracy ◮ Correlations between general and specific: 0.767 (verbal) and 0.646 (matrices) for ability, 0.661 (verbal) and 0.590 (matrices) for items, so the variance of the fast latent variable appears to be consistently higher than the variance of the slow latent variable Analyses with glmer Conclusions ◮ Determine whether the difference in fit is due primarily to the imperfect correlation or to the difference in reliability ◮ Random parameters for both persons and items ◮ The glmer function from lme4 can be used to estimate IR models ◮ Reparameterization of slow and fast accuracy as a general with ordinal items; the ‘difficulty’ is mainly in reshaping the data accuracy and a specific variable for fast accuracy in the appropriate way ◮ Correlations between general and specific: 0.767 (verbal) and ◮ A wider variety of decision trees can lead to a much broader 0.646 (matrices) for ability, 0.661 (verbal) and 0.590 (matrices) for items, so the variance of the fast latent variable appears to be scope of useful psychometric models consistently higher than the variance of the slow latent variable ◮ One substantive result is that fast and slow intelligence can be ◮ For items, a positive relationship between speed: easy items are differentiated with respect to both the processes involved and to the corresponding abilities faster, difficult items take more time. ◮ For persons, results depend on the kind of test: for matrices, successful respondents are slower; for verbal analogies, being relatively more successful with fast responses is positively correlated with overall speed, so it often does not help to use more time.