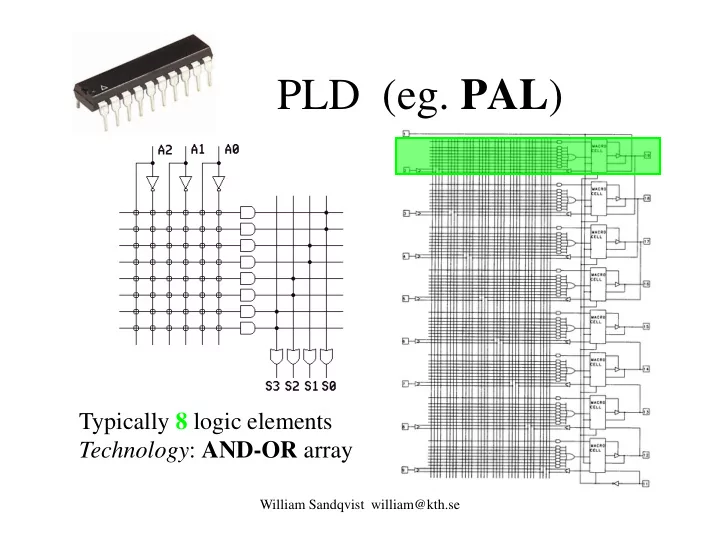

PLD (eg. PAL ) Typically 8 logic elements Technology : AND-OR array William Sandqvist william@kth.se
CPLD (eg. MAX) Typically 64 Macrocells Technology : AND-OR array (larger MAX circuits uses MUX-tree technique) William Sandqvist william@kth.se
Gates with many inputs? CMOS PAL matrix has gates has NAND V DD so many inputs that you have to draw them in a "simplified way" V Q V A Everyone must lead to V B get "0" = slow when there are many inputs V C V SS William Sandqvist william@kth.se
As bad with CMOS NOR CMOS Everyone must lead to get "1" = slow NOR when there are many inputs (one of them must lead to get "0" = fast) William Sandqvist william@kth.se
Fast, but with high power dissipation "Pull-Up" resistor NMOS provides "1" = Fast but "Power NOR Hungry" when output is "0" Can be used for many inputs, but Just one must NMOS will use lead to get "0"? much more power = Fast than the CMOS! William Sandqvist william@kth.se
Large programmable circuits There is therefore a need for other techniques not based on gates with many inputs, in order to be able to build large programmable circuits in CMOS technology! William Sandqvist william@kth.se
FPGA (eg. Cyclone II) Typically 50000 logic elements Technology : MUX tree William Sandqvist william@kth.se
The Multiplexor MUX The multiplexer can select which input you are going to connect to the output. X 1 MUX is now the "standard Z Y 0 component" in the development of Digital Logic. S Z = SX + S Y William Sandqvist william@kth.se
Multiplexer MUX To the right we have a MUX in rope technology - April 1-joke from Scientific American! X 1 Z Y 0 S Z = SX + S Y Did you recognize that it was a MUX that was the "secret" circuit at LAB1? William Sandqvist william@kth.se
Logical functions with MUX How can the following functions be implemented with a 2: 1 X 1 Multiplexer? Z Y 0 = Z x NOT 0 = ⋅ Z x x AND ? S 1 0 = + Z x x OR Z = SX + S Y 1 0 = ⊕ Z x x XOR 1 0 William Sandqvist william@kth.se
Quickie Question … How to connect the inputs of the MUX in order to implement an inverter? Desired function: William Sandqvist william@kth.se
Invertering NOT with MUX Specification: if input = ’1’ then result <= ’0’ if input = ’0’ then result <= ’1’; X x 0 0 1 0 1 Z 1 0 Y 1 0 = ⋅ + ⋅ = Z S X S Y S = ⋅ + ⋅ = x 0 0 x 1 x NOT Input ( x 0 ) 0 0 William Sandqvist william@kth.se
Quickie Question … How to connect the inputs of the MUX in order to implement an and gate? Desired function: William Sandqvist william@kth.se
AND -function with MUX Specification: x 0 0 1 X x 1 x 0 1 0 0 0 Z 1 Y 0 1 0 0 S = 1 ⋅ Z x x AND 0 x 1 = + = ⋅ + ⋅ = ⋅ Z SX S Y x x x 0 x x 1 1 0 1 0 William Sandqvist william@kth.se
OR -function with MUX Specification: x 0 0 1 x 1 X 0 1 0 = 1 + 1 1 Z x x OR 1 0 Z 1 1 Y x 0 0 = + + = S Z x x x x x x 1 0 1 0 0 1 x 1 = + = + + ⋅ = { SX SY } x x ( x ) x x 0 1 1 0 0 = ⋅ + ⋅ x 1 x x 1 1 0 William Sandqvist william@kth.se
XOR -function with MUX Specification: x 0 0 1 X x 1 x 1 0 1 0 0 = 1 ⊕ Z Z x x XOR 1 Y 0 1 0 x 0 0 S = + = Z SX S Y x 1 = ⋅ + ⋅ = ⊕ x x x x x x 0 1 1 0 1 0 William Sandqvist william@kth.se
Hierarchies of muxes x 11 1 x 10 0 1 x 11 11 = Z x 10 10 x 01 0 Z 1 x 01 01 x 00 x 00 00 0 s 1 s 1 s 0 s 0 William Sandqvist william@kth.se
Complex functions with MUXes Choose any of the inputs as address inputs ... z x y 11 00 01 11 10 0 z 10 1 1 0 0 0 = + + f f z x x y zy 01 1 1 0 1 1 0 00 z x y ... And minimize / implement function that occur? For each input. Draw new Karnaugh diagrams if necessary. An ( n + 1)-input function could be implemented with a MUX having n select-inputs! William Sandqvist william@kth.se
Shannon decomposition Claude Shannon mathematician / electrical engineer (1916 –2001) x n f 1 x 1 x n 1 f f x n x 1 f 0 x 0 x 1 x 0 0 William Sandqvist william@kth.se
Shannon decomposition A Boolean function f ( x n , …, x 1 , x 0 ) can be divided to = ⋅ + ⋅ f ( x , ... , x , x ) x f ( x , ... , x , 1 ) x f ( x , ... , x , 0 ) 0 n 1 0 0 n 1 n 1 The function can then be implemented with a multiplexer. x n x n f f 1 x 1 x 1 x 0 1 f x n f 0 x 1 0 x 0 William Sandqvist william@kth.se
Recursively All Boolean functions f ( x n , …, x 1 , x 0 ) can be broken down (recursively) to = ⋅ + ⋅ f ( x , ... , x , x ) x f ( x , ... , x , 1 ) x f ( x , ... , x , 0 ) 0 n 1 0 0 1 n 1 0 n 1 = ⋅ + ⋅ f ( x , ... , x ) x f ( x , ... , x , 1 ) x f ( x , ... , x , 0 ) 1 1 n 1 1 11 n 2 10 n 2 f 11 1 f 1 f 1 f 10 1 0 1 f f f 0 0 f 01 0 f 0 1 f 00 0 x 0 x 0 and so on. f 0000 … x 1 William Sandqvist william@kth.se
Proof = ⋅ + ⋅ f ( x , ... , x , x ) x f ( x , ... , x , 1 ) x f ( x , ... , x , 0 ) 0 n 1 0 0 n 1 n 1 Right hand side: if x 0 =1 so is the right term zero. Then the f is equal to the left term. if x 0 =0 so is the left term zero. Then the f is equal to the right term. Left hand side: if x 0 =1 so is f equal to f ( x n ,..., x 1 ,1) (= left term on right side) if x 0 =0 so is f equal to f ( x n ,..., x 1 ,0) (= right term on right side) LHS=RHS William Sandqvist william@kth.se
MUX networks Value f yz 1 111 1 00 01 11 10 x 0 1 0 1 011 0 0 0 1 1 0 1 0 1 101 0 1 f 001 1 1 0 0 0 One can see xyz as an address, 1 1 110 0 to the squares in the 0 0 010 1 z Karnaughmap. With values 1 y 100 1 1/0 from the squares to the 0 000 0 inputs of the MUX the x function f is realized. Address Address pins William Sandqvist william@kth.se
Look-up-table (LUT) 0/1 Programmable 1 cells 0/1 0 1 f 0 0/1 1 A LUT with n inputs can 0/1 0 realize all combinational functions with n inputs x 2 x 1 Two-input LUT William Sandqvist william@kth.se
LUT for XOR-gate 0 1 x x f 1 2 1 0 1 1 0 1 f 1 0 1 0 1 1 0 1 1 0 0 0 0 0 x 2 x 1 Two-input LUT William Sandqvist william@kth.se
A f B A simple FPGA cell LUT C D The simplest FPGA cell consists of a single Look-Up- Table - LUT, a D flip-flop and a bypass mux. D flip-flop is a memory circuit for synchronization – it will come later in the course. With the bypass mux one can exclude the D flip-flop when not needed. A 0 B LUT 1 S D Q C D M CLK D-flipflop will be explained RESET soon in this course William Sandqvist william@kth.se
LUT function number = = f ( x , x , x , x ) " 0110100110 010110 " f 3 2 1 0 6996 Bit # 1 Bit # 0 Bit # 15 LSB The functions that are MSB stored in a LUT are Do you usually numbered after recognize the number that is made the up of the 1's in the truth function table / Karnaugh map. ...? William Sandqvist william@kth.se
LUT function number = = f ( x , x , x , x ) " 0110100110 010110 " f 3 2 1 0 6996 = ⊕ ⊕ ⊕ f x x x x 6996 3 2 1 0 Now you know which function that has the number 6996 ! With a LUT, all functions are realized, so none of them are more difficult to Odd parity! make than any other! No mergings are possible. William Sandqvist william@kth.se
William Sandqvist william@kth.se
Decoder Mostly used as address decoder Only one output is active when the 'enable' (en) is active The active output is selected with a 1 a 0 en a a y y y y 1 0 0 1 2 3 1 0 0 1 0 0 0 1 0 1 0 1 0 0 y 3 a 0 1 1 0 0 0 1 0 a 1 y 2 1 1 1 0 0 0 1 y 1 0 - - 0 0 0 0 en y 0 2-to-4 decoder William Sandqvist william@kth.se
Demultiplexer The demultiplexer has basically the same function as the decoder, but is drawn differently ... The input is connected to a selected output Now en is f I 0 s s y y y y 1 0 0 1 2 3 namned 1 0 0 1 0 0 0 y 3 I 0 ! 1 0 1 0 1 0 0 y 2 1 1 0 0 0 1 0 I 0 y 1 1 1 1 0 0 0 1 0 - - 0 0 0 0 y 0 s 1 s 0 William Sandqvist william@kth.se
Read-only-memory (ROM) Sel 0 Programable 0/1 0/1 ... 0/1 bits Sel 1 0/1 0/1 ... 0/1 a 0 . a 1 . ... . . a m . . Sel 2m 0/1 0/1 ... 0/1 Threestate En Decoder buffers d n-1 d n-2 ... d 0 William Sandqvist william@kth.se
16:4 Encoder Encoders have the opposite function as a decoder, ie it translates 2 N bit input to a N-bitar code. • The information is concentrated Eg. Keyboard with 16 4-bit HEX-code for the (2 4 ) keys pressed key w 0 y 0 n 2 n inputs outputs y n 1 – w n 1 2 – William Sandqvist william@kth.se
Recommend
More recommend