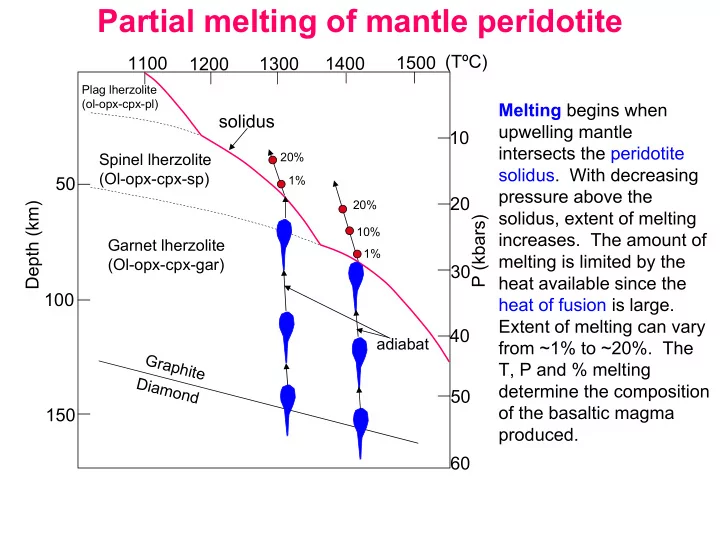

Partial melting of mantle peridotite 1500 (TºC) 1100 1200 1300 1400 Plag lherzolite (ol-opx-cpx-pl) Melting begins when solidus upwelling mantle 10 intersects the peridotite Spinel lherzolite 20% solidus. With decreasing (Ol-opx-cpx-sp) 50 1% pressure above the 20 20% Depth (km) solidus, extent of melting P (kbars) 10% increases. The amount of Garnet lherzolite 1% melting is limited by the (Ol-opx-cpx-gar) 30 heat available since the 100 heat of fusion is large. Extent of melting can vary 40 adiabat from ~1% to ~20%. The G r a p h T, P and % melting i t e Diamond determine the composition 50 of the basaltic magma 150 produced. 60
How does melting occur in the mantle? OL OL OL Olivine G O C Gar O Cpx G O Gar OL C Opx Incr. melt OL Cpx OL OL O Opx OL OL OL OL Melting of garnet lherzolite begins at As the extent of melting increases, cpx-cpx-garnet triple junctions in melt migrates along grain boundaries response to a reduction in pressure. forming an inter-connected network Olivine is not involved in melting at that allows the melt to segregate from early stages. the unmelted crystal residue. Composition of melt depends on the P and T (which controls the extent of melting) and the phases involved in the melting. Suppose that ~1/3 (opx) + ~1/3 (cpx) + ~1/3 (garnet) were melting. Opx and cpx contain ~54% SiO 2 and garnet contains ~ 42% SiO 2 . The melt would contain [1/3(54) +1/3(54) + 1/3(42)]% SiO 2 , i.e., ~ 50% SiO 2 . In other words, magmas formed by mantle melting will contain ~50% SiO 2 ( basalt) .
Schematic view of some processes in basalt formation Eruption of Eruption of primary fractionated magma Flood Basalt magma (± xenoliths) Near-surface magma chamber crustal (+ differentiation) Crust xenoliths Crustal Underplating sill Mantle dike (+ differentiation) mantle sill xenoliths “Failed” eruptions Rapid ascent of magma (cause metasomatism of thru narrow conduit lithosphere) “Trapping” of melt at A – L boundary Lith. (high pressure fractionation) Asth. Diapir Melt accumulation partial melting
Melting and crystallization Understanding the partial melting processes that produce magmas and the subsequent crystallization and differentiation processes that modify these magmas forms the heart of igneous petrogenesis. To understand these processes, it is necessary to understand thermodynamics of macroscopic systems and chemical kinetics. There is a large body of published work that has applied thermodynamic principles to petrogenesis of igneous rocks (and also metamorphic rocks), the most comprehensive work being that of Mark Ghiorso who has, over the past 25 years, developed and refined an algorithm that permits one to calculate details of melting and crystallization processes over a wide range of compositions, temperatures and pressures. This work is encoded in MELTS , an online computer program that will do the requisite complex computations. The basic principle in MELTS involves the fundamental condition for equilibrium, namely that a chemical system of a specific composition at a specific P and T will minimize the total Gibbs Free Energy. Using this principle and a huge library of experimental data obtained over the past century, Mark’s program is applicable over a wide range of temperatures, pressures and compositions. While the implementation of MELTS has “black box” aspects to it, it is a very powerful way to understand melting and crystallization in the earth. In this class, we will not attempt to delve too deeply into the theoretical aspects of melting and crystallization since few in this class have the requisite background, but, rather, we will use experimental data obtained on simple systems to illustrate the processes. One basic rule of thermodynamics that we must understand at the outset is the phase rule, so we will start there.
PHASE EQUILIBRIA AND PHASE DIAGRAMS Experimentally determined phase diagrams are used extensively by petrologists to elucidate the details of crystallization and/or melting phenomena in igneous systems. At the present time there are basically two approaches used by experimental petrologists: [1] Detailed studies of “simple” systems containing fewer than 5 components. These are called model or analog systems. Simple systems have the advantage that the phase equilibria can be accurately expressed in a phase diagram and a large number of compositions can be examined. In addition, compositional variables can be well controlled. The main deficiency of simple systems is that they may not adequately model the phase equilibria occurring in natural systems. [2] Melting and crystallization studies on “real” rocks, i.e., naturally occurring samples. In this approach, the results can be directly applied to the particular rocks being studied but they are limited in the sense that only one composition is being studied. In addition, the fact that real rocks contain at least 10 major components makes the graphical depiction of phase equilibria rather difficult. With modern experimental equipment, petrologists are able to control all the important variables, i.e., T, P, and the partial pressures (actually fugacity) of volatile species such as H 2 O, CO 2 , SO 2 and O 2 . In this introduction to phase equilibria we will consider temperature (T), and composition (X) as the main variables. The appropriate pressure is noted at the top of each diagram.
The Phase Rule At the outset, it is important to know the phase rule which can be written as: f = c - p + 2 where c = number of components , i.e., the minimum number of chemical species that alone, or in varying proportions, define the chemical compositions of all the phases in the system. p = number of phases . A phase is a homogeneous state of matter that is physically separable from other phases in the system. Each mineral type constitutes a phase (even if the mineral is a solid solution), the liquid is a single phase (except in rare cases where liquid immiscibility occurs) and the gas (if present) is a single phase. f = number of degrees of freedom , i.e., the number of variables that can be independently changed without causing a change in the number or types of phases in a system. If either of the variables T or P is held constant, we have the reduced phase rule f = c - p + 1 If both of the variables T and P are held constant, we have the reduced phase rule f = c - p
The Phase Rule (cont.) The phase rule was originally derived from thermodynamic principles by J. Willard Gibbs and hence it is commonly known as the Gibbs Phase Rule . It is widely used in both igneous and metamorphic petrology to predict the number of phases that can be present in equilibrium assemblages. Phase assemblages with zero degrees of freedom are invariant (f = 0) Phase assemblages with one degree of freedom are univariant (f = 1) Phase assemblages with two degrees of freedom are divariant (f = 2) Phase assemblages with three degree of freedom are trivariant (f = 3), etc. Important principles of crystallization and melting can be demonstrated by examining a few, relatively simple, systems. Phase diagrams for one-, two-, three- component and higher order systems are widely used by petrologists to understand and illustrate the details of crystallization and/or melting. It is important to keep in mind, however, that natural systems are compositionally much more complex and will consequently show somewhat more complex behavior.
PHASE EQUILIBRIA AND PHASE DIAGRAMS Before we start looking at simple systems, let’s look at natural examples to provide some context of what it is that we are trying to explain by spending huge amounts of time and energy doing difficult experiments in the lab. 1130ºC 1170ºC Photomicrographs of thin sections of samples collected from variable depths and temperature from Makaopuhi lava lake, Hawaii. Note: 1. Increasing crystallinity with decreasing T 1020ºC 1075ºC 2. Crystallization sequence: ol plag cpx FeTi-ox 3. Color change in glass (increasingly dark to 1075ºC, clear at 1020ºC)
Olivine Clinopyroxene Plagioclase Opaque 1250 Liquidus 1200 1200 1150 1100 T ºC 1100 Melt 1000 Crust 1050 1000 9000 40 60 100 20 80 Solidus 950 % Glass 0 10 0 10 20 30 40 50 0 10 20 30 40 50 0 10 100 Note: (1) olivine increases Olivine Augite Plagioclase Weight % Glass then decreases in amount 90 as X n proceeds. (2) Change in comp n of 80 the phenocrysts as X n 70 proceeds--Ferromag. minerals become 60 increasingly Fe rich and plagioclases become 50 .9 .7 .9 .7 .6 80 70 60 .8 .8 more Na rich Mg / (Mg + Fe) Mg / (Mg + Fe) An
Recommend
More recommend