Parameter Passing Modes a 5 Alternative evaluation schemes b - PowerPoint PPT Presentation

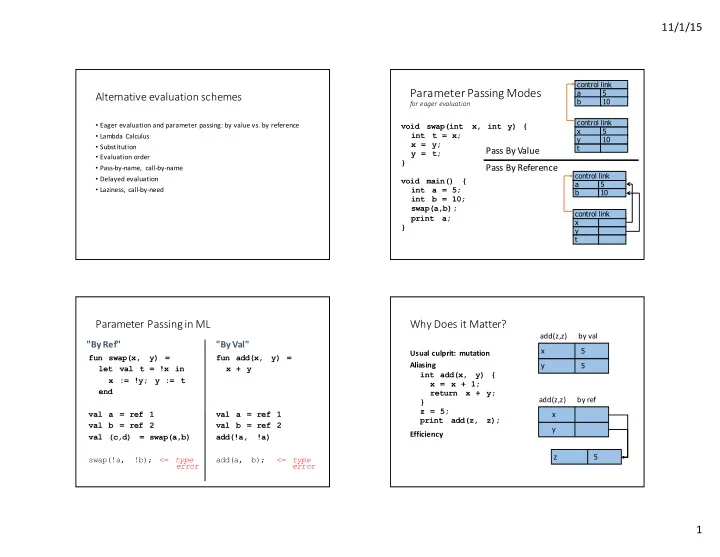
11/1/15 control ¡link Parameter ¡Passing ¡Modes a 5 Alternative ¡evaluation ¡schemes b 10 for ¡eager ¡evaluation control ¡link • Eager ¡evaluation ¡and ¡parameter ¡passing: ¡by ¡value ¡vs. ¡by ¡reference void swap(int x, int y) { x 5 • Lambda ¡Calculus int t = x; y 10 x = y; • Substitution t Pass ¡By ¡Value y = t; • Evaluation ¡order } Pass ¡By ¡Reference • Pass-­‑by-­‑name, ¡ call-­‑by-­‑name control ¡link • Delayed ¡evaluation void main() { a 5 • Laziness, ¡call-­‑by-­‑need int a = 5; b 10 int b = 10; swap(a,b); control ¡link print a; x } y t Parameter ¡Passing ¡in ¡ML Why ¡Does ¡it ¡Matter? add(z,z) ¡ ¡ ¡ ¡ ¡ ¡by ¡val "By ¡Ref" "By ¡Val" x ¡ ¡ ¡ ¡ ¡ 5 Usual ¡culprit: ¡ mutation fun swap(x, y) = fun add(x, y) = Aliasing y ¡ ¡ ¡ ¡ ¡ ¡ 5 let val t = !x in x + y int add(x, y) { x := !y; y := t x = x + 1; end return x + y; add(z,z) ¡ ¡ ¡ ¡ ¡ ¡by ¡ref } z = 5; val a = ref 1 val a = ref 1 x ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ print add(z, z); val b = ref 2 val b = ref 2 y ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ ¡ Efficiency val (c,d) = swap(a,b) add(!a, !a) z ¡ ¡ ¡ ¡ ¡ ¡ 5 swap(!a, !b); <= type add(a, b); <= type error error 1

11/1/15 (lambda) λ calculus Pure ¡Lambda ¡Calculus Terms • "simplest ¡possible ¡functional ¡programming ¡ language" • Reduction (evaluation) ¡by ¡rewriting ¡ function ¡applications ¡to ¡ e ::= substitute arguments ¡in ¡place ¡ of ¡parameters. variables x • Invented ¡by ¡Alonzo ¡Church, ¡1920s/1930s • (of ¡the ¡Church-­‑Turing ¡Thesis ¡and ¡more..., ¡Turing's ¡advisor) • One ¡of ¡3 ¡fundamental ¡models ¡of ¡computation application ¡(left ¡associative) (e e) • Why ¡study? • Essence ¡of ¡functions ( λ x.e) lambda ¡expression • Alternative ¡to ¡environment-­‑based ¡evaluation (think ¡anonymous ¡function) • Understand ¡other ¡choices ¡among ¡alternative ¡evaluation ¡rules. Equivalence/Reduction ¡Rules Su Substitution Rules "substitute ¡ e 1 for ¡all ¡occurrences ¡of ¡ x in ¡ e 2 " [e 1 /x]e 2 ( λ x.e) = ( λ y.[y/x]e) ( 𝜷 -­‑ rename) "replace ¡all ¡occurrence ¡of ¡ x in ¡ e 2 with ¡ e 1 " (alpha) ¡ 𝜷 -­‑equivalence, ¡ 𝜷 -­‑renaming [e/x]x = e Y ou ¡may ¡rename ¡the ¡variable ¡bound ¡by ¡a ¡lambda ¡if ¡you ¡substitute ¡ its ¡new ¡name ¡for ¡its ¡old ¡name ¡in ¡all ¡of ¡its ¡uses ¡in ¡the ¡lambda's ¡body. [e/x]y = y if y ≠ x = [e 2 /x]e 1 ( 𝛾 -­‑ reduce) ( λ x.e 1 )e 2 [e 1 /x](e 2 e 3 ) = (([e 1 /x]e 2 ) ([e/x]e 3 )) (beta) ¡ 𝛾 -­‑equivalence, ¡ 𝛾 -­‑reduction Take ¡care! [e 1 /x]( λ x.e 2 ) = ( λ x.e 2 ) Y ou ¡may ¡reduce ¡a ¡lambda ¡application ¡to ¡the ¡lambda's ¡body ¡if ¡you ¡ substitute ¡the ¡argument ¡for ¡all ¡uses ¡ufthe ¡lambda's ¡parameter. Double-­‑check ¡your ¡ [e 1 /x]( λ y.e 2 ) = ( λ y.[e 1 /x]e 2 ) printed ¡copy [e 1 /x]e 2 means ¡"substitute ¡ e 1 for ¡all ¡occurrences ¡of ¡ x in ¡ e 2 " if y ≠ x and y ∉ FV(e 1 ) or ¡"replace ¡all ¡occurrence ¡of ¡ x in ¡ e 2 with ¡ e 1 ." 2

11/1/15 Illegal ¡reduction: ¡ Why ¡so ¡careful? Careful ¡substitution captures ¡ z (λf. ¡λ z . ¡f ¡(f ¡ z ))(λx. x. ¡ ¡x ¡ x ¡+ ¡ ¡z) à (λ z .(λx. x. ¡ ¡x ¡ x ¡+ ¡ ¡ z )((λx. x. ¡ ¡x ¡ x ¡+ ¡ ¡ z ) ¡ z ) Must ¡be ¡ careful with ¡substitution ¡to ¡avoid ¡ variable ¡capture, à λz. ¡(λx. ¡x ¡+ ¡z)(z ¡+ ¡z) i.e. , ¡ accidentally ¡ attaching ¡variable ¡ uses ¡to ¡wrong ¡definitions. FV( ¡ ¡) ¡= ¡{ z } à λz. ¡(z ¡+ ¡z) ¡+ ¡z Fr Free ¡ ¡Variables Legal ¡ reduction: Variables ¡ used ¡but ¡not ¡bound ¡in ¡a ¡term. 𝜷 -­‑rename ¡ z to ¡ y FV(e) is ¡defined ¡recursively ¡ for ¡lambda ¡calculus ¡terms ¡ e : to ¡avoid ¡capture. (λf. ¡λz. ¡f ¡(f ¡z))(λx. ¡x ¡+ ¡z) à (λf. ¡λ y . ¡f ¡(f ¡ y ))(λx. x. ¡ ¡x ¡ x ¡+ ¡ ¡ z ) FV(x) = {x} à (λ y . ¡(λx. ¡ . ¡x ¡ ¡+ ¡ ¡ z )((λx. ¡ . ¡x ¡ ¡+ ¡ ¡ z ) ¡ y ) FV(e 1 e 2 ) = FV(e 1 ) U FV(e 2 ) à λy. ¡(λx. ¡x ¡+ ¡z)(y ¡+ ¡z) FV( λ x.e) = FV(e) - {x} à λy.(y + ¡z) ¡+ ¡z 𝜃 -reduction Example ¡reduction nice, ¡but ¡optional, ¡rule Left-­‑associative ( λ x.e x) = e ( λ f. λ x.f(f x))( λ z.x+z) 2 ( λ f. λ a.f(f a))( λ z.x+z) 2 (rename x) ([( λ z.x+z)/f] λ a.f(f a)) 2 (reduce f) ( λ a.( λ z.x+z)(( λ z.x+z)a)) 2 (substitution) ( λ a.( λ b.x+b)(( λ z.x+z)a)) 2 (rename z) ( λ a.( λ b.x+b)([a/z](x+z)) 2 (reduce z) ( λ a.( λ b.x+b)(x+a)) 2 (substitution) ( λ a.[(x+a)/b](x+b)) 2 (reduce b) ( λ a.x+(x+a)) 2 (substitution) [2/a](x+(x+a)) (reduce a) x+x+2 (substitution) Normal ¡form: no ¡more ¡reductions ¡possible. 12 3

11/1/15 Normal ¡forms Evaluation/reduction ¡strategies T erm ¡ is ¡in ¡ normal ¡form if ¡no ¡more ¡reductions ¡are ¡ possible. Any ¡order ¡allowed ¡ by ¡the ¡rules ¡is ¡valid: Not ¡all ¡terms ¡can ¡be ¡reduced ¡to ¡a ¡normal ¡form: 𝛻 = ( λ x.(x x)) ( λ x.(x x)) (λx. ¡x ¡+ ¡7) ((λy. ¡ y ¡* ¡4) ¡2) à (λx. ¡x ¡+ ¡7) ¡8 ¡ à 8 ¡+ ¡7 à 15 Confluence: (λx. ¡x ¡+ ¡7)((λy. ¡ y ¡* ¡4) ¡2) à ((λy. ¡ y ¡* ¡4) ¡2) + ¡7 ¡ à 8 ¡+ ¡7 à 15 If ¡ e can ¡be ¡reduced ¡to ¡a ¡normal ¡form, ¡it ¡can ¡be ¡reduced ¡to ¡ exactly ¡one ¡normal ¡form. ¡ ¡Reduction ¡order ¡does ¡not ¡matter. e BUT , ¡not ¡all ¡reduction ¡orders/ ¡ Some ¡evaluation ¡ orders ¡do ¡not ¡lead ¡to ¡normal ¡form. evaluation ¡ strategies ¡ are ¡guaranteed ¡ e 1 e 2 (λx. ¡251) ¡(λx.(x ¡x)) ¡(λx.(x ¡x)) to ¡reach ¡a ¡normal ¡form. N 13 Encodings: ¡natural ¡numbers Encodings: ¡booleans, ¡conditionals (Church ¡numerals) true ¡= ¡ λt. λf. ¡t Numbers ¡ n are ¡functions ¡that ¡compose ¡their ¡first ¡argument ¡ (s ¡ Curried ¡2-­‑argument ¡function ¡returns ¡1 st arg for ¡successor) ¡ n times ¡over ¡their ¡ second ¡argument ¡ (z ¡for ¡zero). false ¡= ¡ λt. λf. ¡f 0 ¡= ¡ λs. λz. ¡z Curried ¡2-­‑argument ¡function ¡returns ¡2 nd arg 1 ¡= ¡ λs. λz. ¡s ¡z 2 ¡= ¡ λs. λz. ¡s ¡(s ¡z) if ¡= ¡ λc. λt. λf. ¡c ¡t ¡f ... Curried ¡3-­‑argument ¡function ¡applies ¡1 st arg (boolean condition) ¡to: n = ¡ λs. λz. ¡s ¡(s ¡(s ¡... ¡(s ¡z) ¡... ¡) ¡) • 2 nd argument ¡(true ¡branch) ¡and ¡ • 3 rd argument ¡(false ¡branch) 4