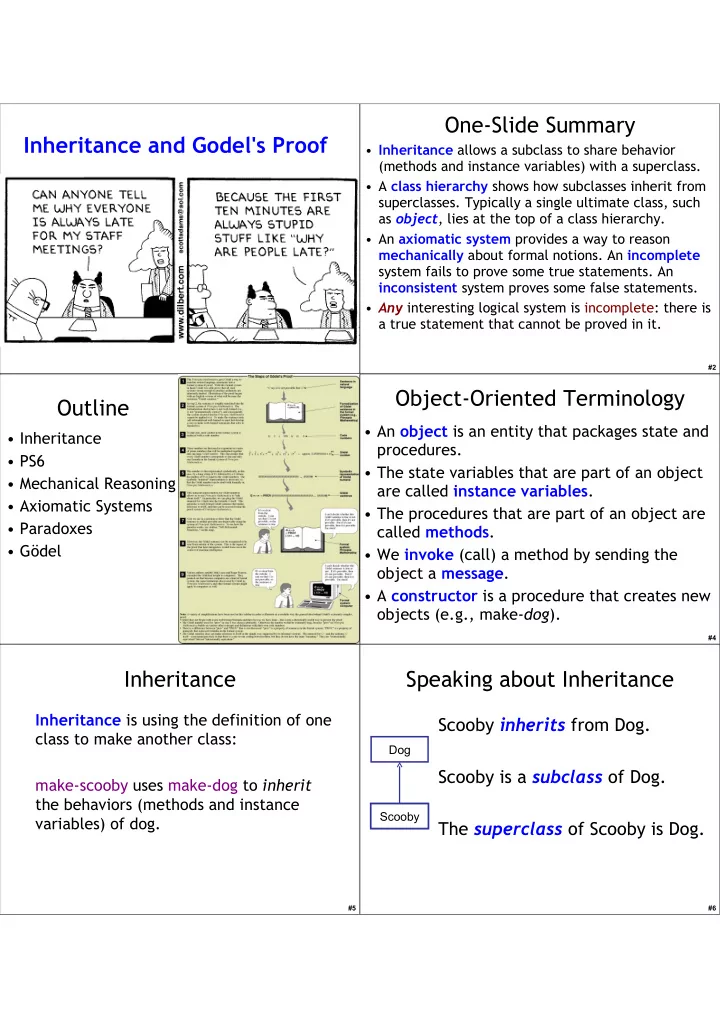
One-Slide Summary Inheritance and Godel's Proof Inheritance allows - PDF document

One-Slide Summary Inheritance and Godel's Proof • Inheritance allows a subclass to share behavior (methods and instance variables) with a superclass. • A class hierarchy shows how subclasses inherit from superclasses. Typically a single ultimate class, such as object , lies at the top of a class hierarchy. • An axiomatic system provides a way to reason mechanically about formal notions. An incomplete system fails to prove some true statements. An inconsistent system proves some false statements. • Any interesting logical system is incomplete: there is a true statement that cannot be proved in it. #2 Object-Oriented Terminology Outline • An object is an entity that packages state and • Inheritance procedures. • PS6 • The state variables that are part of an object • Mechanical Reasoning are called instance variables . • Axiomatic Systems • The procedures that are part of an object are • Paradoxes called methods . • Gödel • We invoke (call) a method by sending the object a message . • A constructor is a procedure that creates new objects (e.g., make- dog ). #3 #4 Inheritance Speaking about Inheritance Inheritance is using the definition of one Scooby inherits from Dog. class to make another class: Dog Scooby is a subclass of Dog. make-scooby uses make-dog to inherit the behaviors (methods and instance Scooby variables) of dog. The superclass of Scooby is Dog. #5 #6

sim-object PS6 PS6 Classes physical-object place Make an adventure game programming with objects make- class is the mobile-object procedure for constructing objects in the Many objects in our game have thing class class person similar properties and student inherits from person police-officer behaviors, so we use which inherits from mobile-object student which inherits from physical-object which inherits from sim-object. inheritance. #7 #8 object PS6 Objects physical-object place Are there class hierarchies like this in the “real Cabal mobile-object Recursa Hall world” or just in fictional (make-place name ) evaluates to an object worlds like thing person that is an instance of the class place. Charlottansville? police-officer student Alyssa P. Hacker #9 #10 RotationPathInterpolator Microsoft Foundation Classes PathInterpolator Interpolator Node Behavior Leaf Object SceneGraphObject Not at all uncommon to have CButton inherits from CWnd inherits from CObject class hierarchies like this! “A button is a kind of window is a kind of object” Java 3D Class Hierarchy Diagram http://java.sun.com/products/java-media/3D/collateral/j3dclass.html #11 #12

Quiz Wednesday Hierarchies • Short Reading Quiz In Class • Designing a class hierarchy is a tricky task • More on it in later CS courses (e.g., 205) #13 #14 Liberal Arts Trivia: Physics Liberal Arts Trivia: Chemistry • Name the vector quantity in physics measured • Give the common name for hydragyrum, a in radians per second. The direction of the heavy metal element. It is the only element vector is perpendicular to the plane of that is liquid at standard temperature and rotation and is usually specified by the “right pressure and is often used in the construction hand rule”. of sphygmomanometers. In the 18 th to 19 th centuries it was used to make felt hats, and the psychological symptoms associated with its poisoning are sometimes used to explain the phrase “mad as a hatter”. • Bonus: What does a sphygmomanometer measure? #15 #16 Story So Far Computer Science/Mathematics • Much of the course so far: • Computer Science (Imperative – Getting comfortable with recursive definitions Knowledge) – Learning to write a program to do (almost) anything (PS1-4) – Are there (well-defined) problems that – Learning more elegant ways of programming cannot be solved by any procedure? (PS5-6) • This Week: Today • Mathematics (Declarative Knowledge) – Getting un - comfortable with recursive – Are there true conjectures that cannot definitions be the shown using any proof? – Understanding why there are some things no program can do! #17 #18

Mechanical Reasoning More Mechanical Reasoning Aristotle (~350BC): Organon • Euclid (~300BC): Elements Codify logical deduction with rules of – We can reduce geometry to a few axioms and inference (syllogisms) derive the rest by following rules • Newton (1687): Philosophiæ Naturalis Every A is a P Principia Mathematica X is an A Premises – We can reduce the motion of objects X is a P Conclusion (including planets) to following axioms (laws) Every human is mortal. mechanically Gödel is human. Gödel is mortal. #19 #20 Mechanical Reasoning • Late 1800s – many mathematicians working on codifying “laws of reasoning” – George Boole, Laws of Thought All true statements – Augustus De Morgan about numbers • Whitehead and Russell, 1911-1913 – Principia Mathematica – Attempted to formalize all mathematical knowledge about numbers and sets #21 #22 Perfect Axiomatic System Incomplete Axiomatic System incomplete Derives Derives all true some, but not all true statements, and no false statements, and no false statements starting from a statements starting from a finite number of axioms finite number of axioms and following mechanical and following mechanical inference rules. inference rules. #23 #24

Principia Mathematica Inconsistent Axiomatic System • Whitehead and Russell (1910– 1913) – Three Volumes, 2000 pages Derives • Attempted to axiomatize mathematical all true reasoning statements, and some false – Define mathematical entities (like numbers) statements starting from a using logic finite number of axioms – Derive mathematical “truths” by following and following mechanical mechanical rules of inference inference rules. – Claimed to be complete and consistent some false statements • All true theorems could be derived • No falsehoods could be derived #25 #26 Russell’s Paradox Russell’s Paradox • Some sets are not members of themselves • S = set of all sets that are not members of themselves – set of all Students • Is S a member of itself? • Some sets are members of themselves – If S is an element of S , then S is a member – set of all things that are not Students of itself and should not be in S . • S = the set of all sets that are not – If S is not an element of S , then S is not a members of themselves member of itself, and should be in S . • Is S a member of itself? #27 #28 Ban Self-Reference? Russell’s Resolution? • Principia Mathematica attempted to Set ::= Set n resolve this paragraph by banning self- reference Set 0 ::= { x | x is an Object } • Every set has a type Set n ::= { x | x is an Object or a Set n - 1 } – The lowest type of set can contain only “objects”, not “sets” – The next type of set can contain objects and S : Set n sets of objects, but not sets of sets Is S a member of itself? #29 #30

Russell’s Resolution? Epimenides Paradox Epimenides (a Cretan): Set ::= Set n “All Cretans are liars.” Set 0 ::= { x | x is an Object } Equivalently: Set n ::= { x | x is an Object or a Set n - 1 } “This statement is false.” S : Set n Russell’s types can help with the Is S a member of itself? set paradox, but not with these. No, it is a Set n so, it can’t be a member of a Set n #31 #32 Liberal Arts Trivia: Liberal Arts Trivia: Woodworking English Literature and Drama • Name the tragedy by Shakespeare parodied • This woodworking joinery technique is noted below by Tatsuya Ishida. for its tensile strength (resistance to being pulled apart). A series of pins are cut from • Bonus points: the blank of animals. the end of one board and interlock with a series of tails cut into the end of another. Once glued it requires no fasteners. #33 #34 Gödel’s Solution Kurt Gödel • Born 1906 in Brno (now Czech Republic, then All consistent axiomatic formulations of Austria-Hungary) number theory include undecidable • 1931: publishes Über propositions. formal unentscheidbare (GEB, p. 17) Sätze der Principia Mathematica und undecidable – cannot be proven either verwandter Systeme ( On true or false inside the system. Formally Undecidable Propositions of Principia Mathematica and Related Systems ) #35 #36

Gödel’s Theorem • 1939: flees Vienna • Institute for Advanced Study, In the Principia Mathematica Princeton system, there are statements that • Died in 1978 – cannot be proven either true or convinced false. everything was poisoned and refused to eat #37 #38 Gödel’s Theorem Gödel’s Theorem All logical systems of any In any interesting rigid system, complexity are incomplete : there are statements that are there are statements that cannot be proven either true or false. true that cannot be proven within the system. #39 #40 Proof – General Idea Gödel’s Statement •Theorem: In the Principia G : This statement does not have any proof in the Mathematica system, there system of Principia are statements that cannot be Mathematica . proven either true or false. •Proof: Find such a statement! G is unprovable, but true! Why? #41 #42

Gödel’s Proof Idea Homework G : This statement does not have any • Read Chapter 11 proof in the system of PM . • Short In-Class Quiz Wednesday • PS6 Due Mon Mar 23 If G is provable, PM would be inconsistent. If G is unprovable, PM would be incomplete. Thus, PM cannot be complete and consistent! #43 #44