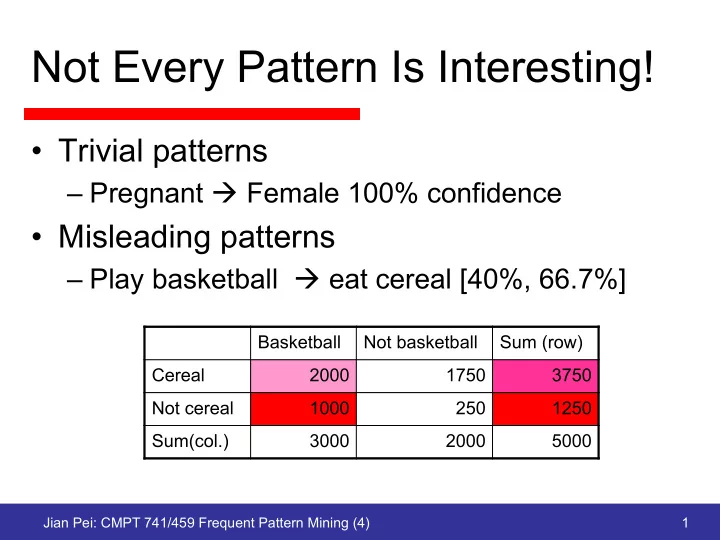

Not Every Pattern Is Interesting! • Trivial patterns – Pregnant à Female 100% confidence • Misleading patterns – Play basketball à eat cereal [40%, 66.7%] Basketball Not basketball Sum (row) Cereal 2000 1750 3750 Not cereal 1000 250 1250 Sum(col.) 3000 2000 5000 Jian Pei: CMPT 741/459 Frequent Pattern Mining (4) 1
Evaluation Criteria • Objective interestingness measures – Examples: support, patterns formed by mutually independent items – Domain independent • Subjective measures – Examples: domain knowledge, templates/ constraints Jian Pei: CMPT 741/459 Frequent Pattern Mining (4) 2
Correlation and Lift • P(B|A)/P(B) is called the lift of rule A à B A , B = P ( A ∪ B ) P ( AB ) corr P ( A ) P ( B ) = P ( A ) P ( B ) • Play basketball à eat cereal (lift: 0.89) • Play basketball à not eat cereal (lift: 1.33) Contingency table Basketball Not basketball Sum (row) B B Cereal 2000 1750 3750 A f 11 f 10 f 1+ Not cereal 1000 250 1250 A f 01 f 00 f 0+ Sum(col.) 3000 2000 5000 f +1 f +0 N Jian Pei: CMPT 741/459 Frequent Pattern Mining (4) 3
Property of Lift • If A and B are independent, lift = 1 • If A and B are positively correlated, lift > 1 • If A and B are negatively correlated, lift < 1 • Limitation: lift is sensitive to P(A) and P(B) { } { } p p r r lift(p, q) < lift(r, s)! q 880 50 930 s 20 50 70 q 50 20 70 s 50 880 930 930 70 1000 70 930 1000 Jian Pei: CMPT 741/459 Frequent Pattern Mining (4) 4
Leverage • The difference between the observed and expected joint probability of XY assuming X and Y are independent leverage ( X → Y ) = P ( XY ) − P ( X ) P ( Y ) • An “absolute” measure of the surprisingness of a rule – Should be used together with lift Jian Pei: CMPT 741/459 Frequent Pattern Mining (4) 5
Convinction • The expected error of a rule conv ( X → Y ) = P ( X ) P ( ¯ Y ) 1 = P ( X ¯ lift ( X → ¯ Y ) Y ) • Consider not only the joint distribution of X and Y Jian Pei: CMPT 741/459 Frequent Pattern Mining (4) 6
Odds Ratio P ( XY ) = P ( XY ) P ( X ) odds ( Y | X ) = P ( X ¯ P ( X ¯ Y ) Y ) P ( X ) P ( ¯ XY ) = P ( ¯ XY ) P ( ¯ X ) odds ( Y | ¯ X ) = P ( ¯ X ¯ P ( ¯ X ¯ Y ) Y ) P ( ¯ X ) X ) = P ( XY ) · P ( ¯ X ¯ oddsratio ( X → Y ) = odds ( Y | X ) Y ) odds ( Y | ¯ P ( X ¯ Y ) · P ( ¯ XY ) Jian Pei: CMPT 741/459 Frequent Pattern Mining (4) 7
χ 2 • Suppose attribute A has c distinct values a 1 , … , a c and attribute B has r distinct values b 1 , … , b r • The χ 2 value (Pearson χ 2 statistics) is c r ( o ij − e ij ) 2 χ 2 = X X e ij i =1 j =1 – o ij and e ij are the observed frequency and the expected frequency, respectively, of the joint event a i b j , respectively Jian Pei: CMPT 741/459 Frequent Pattern Mining (4) 8
Example χ 2 = (2000 − 2250) 2 + (1750 − 1500) 2 + (1000 − 750) 2 + (250 − 500) 2 = 277 . 8 2250 1500 750 500 • The χ 2 value is greater than 1 • count(basketball, cereal) = 2000 < expectation (2250) à play basketball and eating cereal are negatively correlated Basketball Not basketball Sum (row) Cereal 2000 1750 3750 Not cereal 1000 250 1250 Sum(col.) 3000 2000 5000 Jian Pei: CMPT 741/459 Frequent Pattern Mining (4) 9
Φ -coefficient φ = P ( AB ) P ( ¯ A ¯ B ) − P ( ¯ AB ) P ( A ¯ B ) P ( A ) P ( B ) P ( ¯ A ) P ( ¯ p B ) • –1: if A and B perfectly negatively correlated • 1: if A and B perfectly positively correlated • 0: if A and B statistically independent • Drawback: Φ -coefficient puts the same weight on co-occurrence and co-absence Jian Pei: CMPT 741/459 Frequent Pattern Mining (4) 10
IS Measure P ( A, B ) p IS ( A, B ) = lift ( A, B ) P ( A, B ) = p P ( A ) P ( B ) • Biased on frequent co-occurrence • Equivalent to cosine similarity for binary variables (bit vectors) • Geometric mean of rules between a pair of binary random variables s P ( A, B ) P ( A, B ) p IS ( A, B ) = = conf ( A → B ) conf ( B → A ) P ( A ) P ( B ) • Drawback: the value depends on P(A) and P(B) – Similar drawbacks in lift Jian Pei: CMPT 741/459 Frequent Pattern Mining (4) 11
More Measures • All confidence: min{ P(A|B), P(B|A) } • Max confidence: max{ P(A|B), P(B|A) } • The Kulczynski measure: ½ (P(A|B) + P(B| A) Jian Pei: CMPT 741/459 Frequent Pattern Mining (4) 12
Comparing Measures Milk No Milk Sum (row) Contingency table Coffee m, c ~m, c c No Coffee m, ~c ~m, ~c ~c Sum(col.) m ~m Σ Transaction databases and their contingency tables Data Set mc mc mc mc lift all conf. max conf. Kulc. cosine χ 2 D 1 10,000 1,000 1,000 100,000 90557 9.26 0.91 0.91 0.91 0.91 D 2 10,000 1,000 1,000 100 0 1 0.91 0.91 0.91 0.91 D 3 100 1,000 1,000 100,000 670 8.44 0.09 0.09 0.09 0.09 D 4 1,000 1,000 1,000 100,000 24740 25.75 0.5 0.5 0.5 0.5 D 5 1,000 100 10,000 100,000 8173 9.18 0.09 0.91 0.5 0.29 D 6 1,000 10 100,000 100,000 965 1.97 0.01 0.99 0.5 0.10 χ 2 and lift do not perform well on those data sets, since they are sensitive to ~m~c Jian Pei: CMPT 741/459 Frequent Pattern Mining (4) 13
Imbalance Ration • Assess the imbalance of two itemsets A and B in rule implications | P ( A ) − P ( B ) | IR ( A, B ) = P ( A ) + P ( B ) − P ( A ∪ B ) Jian Pei: CMPT 741/459 Frequent Pattern Mining (4) 14
Properties of Measures • Symmetry: is M(A à B) = M(B à A) • Null-transaction dependent (null addition invariant): is ~A~B used in the measure? • Inversion invariant: the value does not change if f 11 and f 10 are exchanged with f 00 and f 01 • Scaling: whether the measure remains if the contingency table [f 11 , f 10 , f 01 , f 00 ] is changed to [k 1 k 3 f 11 , k 2 k 3 f 10 , k 1 k 4 f 01 , k 2 k 4 f 00 ]? Jian Pei: CMPT 741/459 Frequent Pattern Mining (4) 15
Measuring 3 Random Variables • 3 dimensional contingency table c b b c b b a f 111 f 101 f 1+1 a f 110 f 100 f 1+0 a f 011 f 001 f 0+1 a f 010 f 000 f 0+0 f +11 f +01 f ++1 f +10 f +00 f ++0 • For a k-itemset {i 1 , i 2 , … , i k }, the condition for statistical independence is f i 1 i 2 ··· i k = f i 1 + ··· + f + i 2 ··· + · · · f ++ ··· i k N k − 1 Jian Pei: CMPT 741/459 Frequent Pattern Mining (4) 16
Measuring More Random Variables • Some measures, such as lift and statistical independence, can be extended N k − 1 f i 1 i 2 ··· i k I = f i 1 + ··· + f + i 2 ··· + · · · f + ··· + i k PS = f i 1 i 2 ··· i k − f i 1 + ··· + f + i 2 ··· + · · · f + ··· + i k N k N Jian Pei: CMPT 741/459 Frequent Pattern Mining (4) 17
Simpson’s Paradox • A trend that appears in different groups of data disappears when these groups are combined, and the reverse trend appears for the aggregate data – Also known as Yule-Simpson effect – Often encountered in social-science and medical-science statistics – Particularly confounding when frequency data are unduly given causal interpretations Jian Pei: CMPT 741/459 Frequent Pattern Mining (4) 18
Kidney Stone Treatment Example Treatment A Treatment B Small stones G1: 81/87=93% G2: 234/270=87% Large stones G3: 192/263=73% G4: 55/80=69% Overall 273/350=78% 289/350=83% • Which treatment, A or B, is better? Jian Pei: CMPT 741/459 Frequent Pattern Mining (4) 19
Berkeley Gender Bias Case Applicants Admitted Men 8442 44% Women 4321 35% Department Men Women Applicants Admitted Applicants Admitted A 825 62% 108 82% B 560 63% 25 68% C 325 37% 593 34% D 417 33% 375 35% E 191 28% 393 24% F 272 6% 341 7% Jian Pei: CMPT 741/459 Frequent Pattern Mining (4) 20
Fisher Exact Test • Directly test whether a rule X à Y is productive by comparing its confidence with those of its generalizations W à Y, where W is a subset of X – Let X = W U Z W Y Not Y Z a b a + b Not Z c d c + d a + c b + d Sup(W) a = sup ( WZY ) = sup ( XY ) , b = sup ( WZ ¯ Y ) = sup ( X ¯ Y ) c = sup ( W ¯ ZY ) , d = sup ( W ¯ Z ¯ Y ) Jian Pei: CMPT 741/459 Frequent Pattern Mining (4) 21
Marginals • Row marginals a + b = sup ( WZ ) = sup ( X ) , c + d = sup ( W ¯ Z ) • Column marginals a + c = sup ( WY ) , b + d = sup ( W ¯ Y ) a a + b = ad b a + b oddratio = c bc c + d d W Y Not Y c + d Z a b a + b Not Z c d c + d a + c b + d Sup(W) Jian Pei: CMPT 741/459 Frequent Pattern Mining (4) 22
Hypothesis • H 0 : Z and Y are independent given W – X à Y is not productive given W à Y • If Z and Y are independent, then a = ( a + b )( a + c ) , b = ( a + b )( b + d ) oddratio = ad n n bc = 1 c = ( c + d )( a + c ) , d = ( c + d )( b + d ) n n W Y Not Y Z a b a + b Not Z c d c + d a + c b + d Sup(W) Jian Pei: CMPT 741/459 Frequent Pattern Mining (4) 23
Relation between a and b, c, d • Assumption: the row and column marginals are fixed • The value of a uniquely determines b, c, and d W Y Not Y Z a b a + b Not Z c d c + d a + c b + d Sup(W) Jian Pei: CMPT 741/459 Frequent Pattern Mining (4) 24
Recommend
More recommend