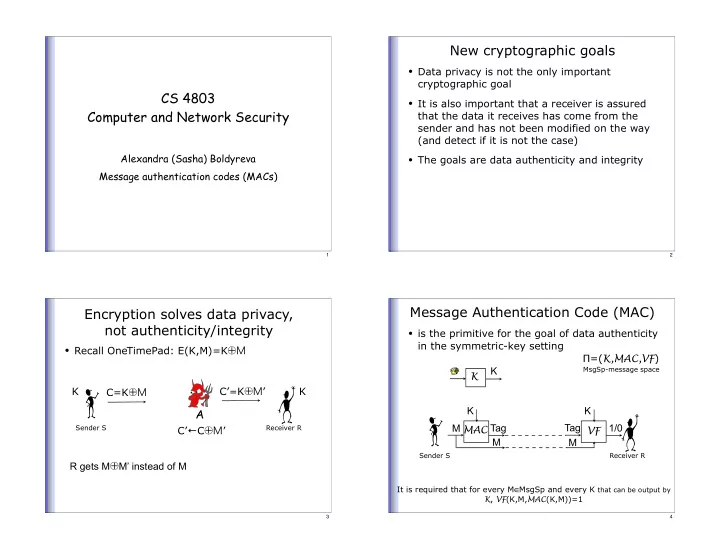
New cryptographic goals Data privacy is not the only important - PowerPoint PPT Presentation

New cryptographic goals • Data privacy is not the only important cryptographic goal CS 4803 • It is also important that a receiver is assured Computer and Network Security that the data it receives has come from the sender and has not been modified on the way (and detect if it is not the case) Alexandra (Sasha) Boldyreva • The goals are data authenticity and integrity Message authentication codes (MACs) 1 2 Message Authentication Code (MAC) Encryption solves data privacy, not authenticity/integrity • is the primitive for the goal of data authenticity in the symmetric-key setting • Recall OneTimePad: E(K,M)=K ⊕M � =( K,MAC,VF ) K MsgSp-message space K K C’ = K ⊕M ’ K C=K ⊕M K K A M Tag Tag 1/0 Sender S Receiver R MAC C’ � C ⊕M ’ VF M M Sender S Receiver R R gets M ⊕ M’ instead of M It is required that for every M ∈ MsgSp and every K that can be output by K , VF (K,M, MAC (K,M))=1 3 4

⊕ ⊕ ⊕ Message Authentication Code (MAC) Towards a security definition for MACs • If the key-generation algorithm simply picks a • We imagine that an adversary can see some random string from some KeySp, then KeySp number of message plus tag pairs describes K • As usual, it is necessary but not sufficient to require that no adversary can compute the • If the MAC algorithm is deterministic, then the secret key verification algorithm VF does not have to be defined as it simply re-computes the MAC by • Right now we will not be concerned with replay invoking the MAC algorithm on the given attacks message M and accepts iff the result is equal to • We don’t want an adversary to be able to its input TAG. compute a new message and a tag such that the receiver accepts (outputs 1). 5 6 Security definition for MACs Examples Fix � =( K ,MAC,VF) Let E:{0,1}k � {0,1}n � {0,1}n be a block cipher. � 1 =({0,1}k , MAC,Vf): Run K to get K For an adversary A consider an experiment Exp-uf-cma( � , A) M[1] M[2] M[m] MAC(K,M): MAC (K, � ) EK EK EK VF (K, � , � ) A Tag= C[1] C[2] C[m] M,Tag Is � 1 secure (uf-cma)? The uf-cma advantage of A is defined as the probability of A outputting M, Tag, s.t. Tag is valid (VF(K,M,Tag)=1) and M is new (was not queried to the MAC oracle) 7 8

⊕ ⊕ ⊕ Note CBC-MAC • We broke the MAC scheme without breaking the Let E:{0,1}k � {0,1}n � {0,1}n be a block cipher. CBC-MAC=({0,1}k ,MAC ): MsgSp={0,1}nm for some m � 1. underlying block cipher (it can be secure PRF). 0n • The weaknesses were in the scheme, not the M[1] M[2] M[m] tools MAC(K,M): EK EK EK C[1] C[2] C[m] MAC returns Theorem. If E is a PRF then CBC-MAC is uf-cma. 9 10 Can we get it all? Can we use a hash function as a building block? • We know how to achieve data privacy (IND-CPA security) • SHA1: {0,1} < � {0,1}160 264 and data authenticity/integrity (UF-CMA security) • Collision-resistant: hard to find M,M’ s.t. SHA1(M)=SHA1(M’) separately. • Is it a good idea to use SHA1 as a MAC? • Can we achieve the both goals at the same time (can we send messages securely s.t. a sender is assured in their • What about: authenticity/integrity)? • MACK(M)=SHA1(M||K)? • Can we use the existing primitives: encryption schemes • MACK(M)=SHA1(K||M)? and MACs? • MACK(M)=SHA1(K||M||K)? • Cannot prove security for these constructions. • Secure construction: HMAC • HMACK(M)=SHA1(K ⊕c ||SHA1(K ⊕d ||M)), where c,d are some constants 11 12

Composite schemes Integrity of encryption • Fix a symmetric encryption scheme and a • We did not define a notion of integrity of encryption schemes (we did it for MACs) message authentication code • But one can define a similar notion for encryption • There are several ways to use them together • Informally, no efficient adversary should be able to 1. Encrypt-and-MAC construct a ciphertext that the receiver will assume valid 2. MAC-then-Encrypt 3. Encrypt-then-MAC • If the components are secure, are the composite schemes secure (provide privacy and integrity)? 13 14 Encrypt-and-MAC MAC-then-Encrypt • Fix a symmetric encryption scheme • Fix a symmetric encryption scheme SE = ( K e , E , D ) SE = ( K e , E , D ) and a MAC and a MAC MAC = ( K m , T , V ) MAC = ( K m , T , V ) • Consider a symmetric encryption scheme • Consider a symmetric encryption scheme EaM = ( K , E , D ) MtE = ( K , E , D ) K K $ $ K e K e ← K e ← K e $ $ K m K m ← K m ← K m Theorem1. There exist an IND-CPA SE and UF-CMA MAC Theorem2. There exist an IND-CPA SE and UF-CMA MAC s.t. EaM constructed as above is NOT IND-CPA secure. s.t. MtE constructed as above is NOT IND-CCA secure. 15 16

Encrypt-then-MAC ! • It’s possible to construct a secure symmetric encryption scheme that provably provides privacy and integrity without using a generic composition. • Fix a symmetric encryption scheme SE = ( K e , E , D ) and a MAC MAC = ( K m , T , V ) • • Consider a symmetric encryption scheme EtM = ( K , E , D ) ;&<'= ;&<*= ;&<,- ' = ;&<, = ... "%2 34%5678, K A925% $ K e ← K e ,(& ⊕ )& ⊕ (& ⊕ ) *(& ⊕ ) +,-'.(& ⊕ ) ,(& ⊕ ) $ ⊕ ⊕ ⊕ ⊕ ⊕ K m ( !"#$ ⋅ ( ← K m ⊕ > ? > ? > ? > ? > ? > ? ... @0$ ) ⊕ (& ⊕ ) *(& ⊕ ) +,-'.(& ⊕ ) ⊕ ⊕ ⊕ 549: τ Theorem3. For every IND-CPA SE and UF-CMA 3<'= 3<* = 3<,- ' = 3<,= /01 ... deterministic MAC , EtM constructed as above provably provides privacy (IND-CPA, IND-CCA) and integrity 34%5678,&B&;<'=& ⊕ ;<*=& ⊕ C ⊕ ;<,-'=& ⊕ 3<,=DE& ⊕ @0$ (&B&> ? + ! . 17 18