nearly free electron approxima0on Bloch equa0on E ! ( b p - PowerPoint PPT Presentation

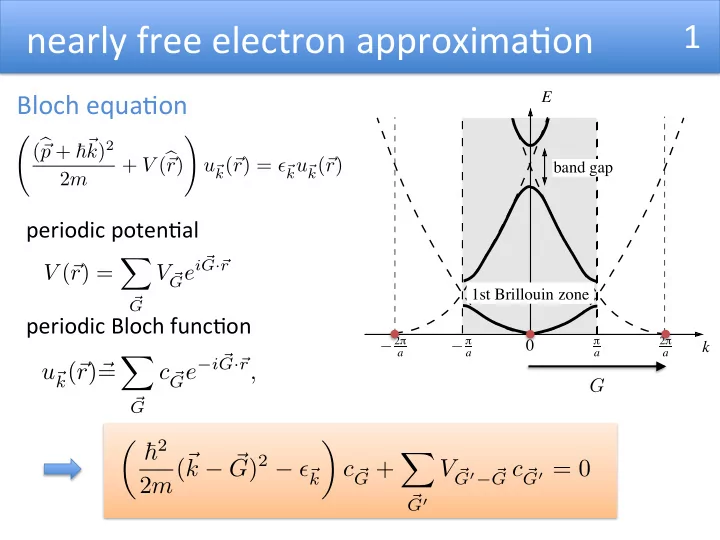
1 ¡ nearly ¡free ¡electron ¡approxima0on ¡ Bloch ¡equa0on ¡ E ! ( b p + ~ ~ k ) 2 ~ + V ( b r ) k ( ~ r ) = ✏ ~ k ( ~ r ) ~ u ~ k u ~ band gap 2 m periodic ¡poten0al ¡ G e i ~ X G · ~ r V ( ~ r ) = V ~ 1st Brillouin zone ~ G periodic ¡Bloch ¡func0on ¡ − 2 � 2 � − � � 0 k a a a a G e − i ~ X G · ~ r , k ( ~ r ) ~ = c ~ u ~ G ~ G ✓ ~ 2 ◆ X 2 m ( ~ k − ~ G ) 2 − ✏ ~ G + G 0 = 0 c ~ V ~ G c ~ G 0 − ~ k ~ G 0

0ght-­‑binding ¡approxima0on ¡ 2 ¡ atom ¡at ¡posi0on ¡ ~ star0ng ¡point: ¡ ¡atomic ¡limit ¡ R ˆ p 2 ~ H a ( ~ r − ~ H a ( ~ r − ~ r − ~ R ) = 2 m + V a ( ~ R ) R ) � n ( ~ R ) = ✏ n � n ( ~ R ) V ¡ regular ¡array ¡of ¡atoms ¡ R ¡ r ¡ ˆ p 2 ~ X r − ~ = 2 m + V a ( ~ R j ) H ~ R j = H a ( ~ R ) + ∆ V ~ R ( ~ r ) Δ V R ¡ R ¡ r ¡ r − ~ X R j ( ~ r ) = V a ( ~ R j 0 ) ∆ V ~ R j 0 6 = ~ ~ R

0ght-­‑binding ¡approxima0on ¡ 3 ¡ Linear ¡combina0on ¡of ¡atomic ¡orbitals ¡(LCAO) ¡ 1 e i ~ k · ~ r − ~ Bloch ¡func0on ¡ X R j � ˜ ˜ k ( ~ r ) = n ( ~ R j ) n ~ √ N ~ R j = 1 Z Z norm: ¡ d 3 re i ~ k · ( ~ R j 0 � ~ n 0 ( ~ d 3 r ˜ X R j ) � ⇤ r � ~ r � ~ r ) ⇤ ˜ h 1 i ˜ k ) = k ( ~ k ( ~ r ) n ( ~ R j ) � ˜ n 0 ( ~ R j 0 ) n ˜ n ~ n 0 ~ ˜ N R j , ~ ~ R j 0 Z d 3 re � i ~ k · ~ X r � ~ R j � ⇤ = n ( ~ R j ) � ˜ n 0 ( ~ r ) ˜ ~ R j e � i ~ k · ~ X n 0 ( ~ R j ↵ ˜ ↵ nn 0 ( ~ n 0 + = � ˜ R j ) R ) ⌧ 1 n ˜ n ˜ ~ R j 6 =0 Hamiltonian: ¡ = 1 Z d 3 re i ~ k · ( ~ R j 0 � ~ n 0 ( ~ X R j ) � ⇤ r � ~ R j ) { H a ( ~ r � ~ h H i ˜ k ) n ( ~ R j 0 ) + ∆ V ~ R j 0 ( ~ r ) } � ˜ n 0 ( ~ R j 0 ) n ˜ ˜ N R j , ~ ~ R j 0 e � i ~ k · ~ n 0 ( ~ n 0 ( ~ X R j � ˜ n 0 + = E ˜ n 0 h 1 i ˜ k ) + ∆ E ˜ R j ) n ˜ n ˜ n ˜ ~ R j 6 =0 Z Z n 0 ( ~ r − ~ d 3 r � ∗ d 3 r � ∗ n 0 = R j ) = n ( ~ R j ) ∆ V ~ R j 0 =0 ( ~ r ) � ˜ n 0 ( ~ r ) ∆ E ˜ n ( ~ r ) ∆ V ~ R j 0 =0 ( ~ r ) � ˜ n 0 ( ~ r ) � ˜ n ˜ n ˜ ˜ ˜

0ght-­‑binding ¡approxima0on ¡ 4 ¡ h i energy ¡spectrum ¡ n 0 ( ~ n 0 ( ~ h H i ˜ k ) � ✏ ~ k h 1 i ˜ k ) = 0 det n ˜ n ˜ band ¡structure ¡of ¡s-­‑orbitals ¡in ¡simple ¡cubic ¡laEce ¡ � s ( ~ r ) = � s ( r ) nearest ¡ ¡ ~  − t R j neighbors ¡  -­‑t ¡ � ss ( ~ -­‑t’ ¡ R j ) = next-­‑nearest ¡ ¡ ~ − t 0  R j neighbors ¡ -­‑t ¡ n.n. n.n.n. e � i ~ k · ~ e � i ~ k · ~ X X R j − t 0 R j = E s + ∆ E s − t ✏ ~ k ~ ~ R j R j = E s + ∆ E s − 2 t { cos( k x a ) + cos( k y a ) + cos( k z a ) } − 4 t 0 [cos( k x a ) cos( k y a ) + cos( k y a ) cos( k z a ) + cos( k z a ) cos( k x a ) }

0ght-­‑binding ¡approxima0on ¡ 5 ¡ band ¡structure ¡of ¡p-­‑orbitals ¡in ¡simple ¡cubic ¡laEce ¡ � x ( ~ r ) = x ' ( r ) , � y ( ~ r ) = y ' ( r ) , � z ( ~ r ) = z ' ( r ) next- nearest neighbors nearest neighbors Important: ¡ phase ¡structure ¡ of ¡wave ¡func0on ¡ " - bonding -­‑ ¡ + ¡ p -­‑orbital ¡ ! - bonding no coupling

0ght-­‑binding ¡approxima0on ¡ 6 ¡ band ¡structure ¡of ¡p-­‑orbitals ¡in ¡simple ¡cubic ¡laEce ¡  t 00 sin( k x a ) sin( k y a ) t 00 sin( k x a ) sin( k z a )  E x ( ~ � 4˜ � 4˜ k ) t 00 sin( k x a ) sin( k y a ) t 00 sin( k y a ) sin( k z a ) E y ( ~ � 4˜ � 4˜ n 0 = h H i ˜ k )   n ˜   t 00 sin( k x a ) sin( k z a ) t 00 sin( k y a ) sin( k z a ) E z ( ~ � 4˜ � 4˜ k ) E x ( ~ k ) = E p + ∆ E p + 2 t cos( k x a ) − 2 t 0 (cos( k y a ) + cos( k z a )) t 0 cos( k y a ) cos( k z a ) + 4˜ t cos( k x a )(cos( k y a ) + cos( k z a )) − 4˜ ~ k · ~ -­‑ ¡approxima0on ¡at ¡ Γ -­‑point ¡( k =0) ¡ p  Ak 2 x + B ( k 2 y + k 2  z ) Ck x k y Ck x k z Ak 2 y + B ( k 2 z + k 2 n 0 = E Γ + x ) h H i ˜ Ck x k y Ck y k z n ˜   Ak 2 z + B ( k 2 x + k 2 y ) Ck x k z Ck y k z

0ght-­‑binding ¡approxima0on ¡ 7 ¡ energy ¡bands ¡in ¡1 st ¡BZ ¡ s-orbitals t 0 = 0 . 2 t p-orbitals t 0 = 0 . 2 t t 0 = 0 . 05 t ˜ t 00 = 0 . 15 t ˜ ˜ t = 0 . 1 t