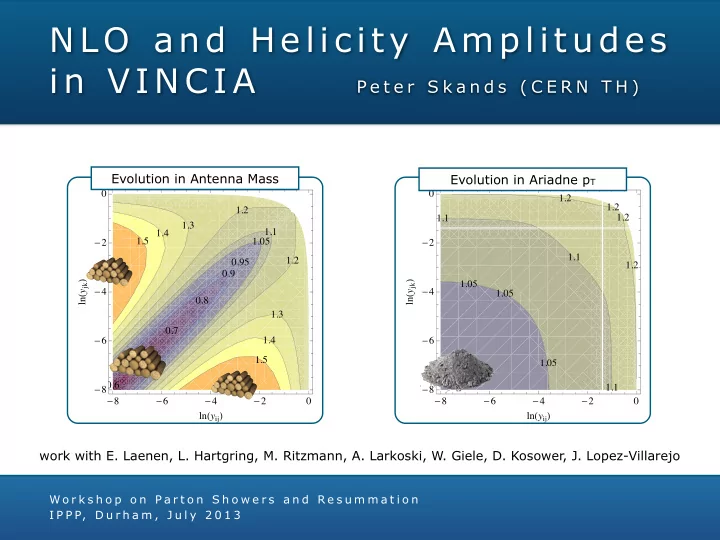

N LO an d H e lic i ty Am p l i t u d es i n VIN C IA P e t e r S k a n d s ( C E R N T H ) Evolution in Antenna Mass Evolution in Ariadne p T Q E = m D H strong L Q E = 2 p T H strong L 0 0 1.2 1.2 1.2 1.2 1.1 1.3 1.1 1.4 1.5 1.05 - 2 - 2 1.1 1.2 0.95 1.2 0.9 ln H y jk L ln H y jk L 1.05 - 4 - 4 1.05 0.8 1.3 0.7 - 6 1.4 - 6 1.5 1.05 0.6 1.1 - 8 - 8 - 8 - 6 - 4 - 2 0 - 8 - 6 - 4 - 2 0 ln H y ij L ln H y ij L work with E. Laenen, L. Hartgring, M. Ritzmann, A. Larkoski, W. Giele, D. Kosower, J. Lopez-Villarejo W o r k s h o p o n P a r t o n S h o w e r s a n d R e s u m m a t i o n I P P P, D u r h a m , J u l y 2 0 1 3
VINCIA Written as a Plug-in to PYTHIA 8 Current Version: VINCIA 1.1.00 C++ (~20,000 lines) Virtual Numerical Collider with Interleaved Antennae Giele, Kosower, Skands, PRD 78 (2008) 014026, PRD 84 (2011) 054003 i Gehrmann-de Ridder, Ritzmann, Skands, PRD 85 (2012) 014013 1 1 j i I k Based on antenna factorization j I k K - of Amplitudes (exact in both soft and collinear limits) m+1 m+1 - of Phase Space (LIPS : 2 on-shell → 3 on-shell partons, with (E,p) cons) K 1.0 0.6 0.8 Resolution Time 0.6 y jk 1.0 p T 0.4 0.8 0.2 Infinite family of continuously deformable Q E 0.8 0.2 0.2 ⌦ ↵ 0.4 0.6 0.8 0.4 0.0 y jk Special cases: transverse momentum, dipole mass, energy 0.0 0.2 0.4 0.6 0.8 1.0 m D 0.4 0.8 1.0 y ij 0.6 0.6 0.8 0.2 0.4 0.2 0.6 0.0 0.0 0.2 0.4 0.6 0.8 1.0 y jk y ij 0.4 E g 0.6 Radiation functions 0.2 0.2 0.8 0.0 0.4 0.0 0.2 0.4 0.6 0.8 1.0 y ij Arbitrary non-singular coefficients, ant i ∗ √ 2 (c) + Massive antenna functions for massive fermions (c,b,t) Kinematics maps Formalism derived for arbitrary 2 → 3 recoil maps, κ 3 → 2 Default: massive generalization of Kosower’s antenna maps vincia.hepforge.org 2 P. S k a n d s
Matrix-Element Matching Standard Paradigm: Double counting, IR divergences, multiscale logs Have ME for X, X+1,…, X+n; Want to combine and add showers → “The Soft Stuff” Works pretty well at low multiplicities Q cut |M X | 2 Still, only corrected for “hard” scales; Soft still pure LL. At high multiplicities: |M X+1 | 2 Showers Efficiency problems: slowdown from need to compute and Matching generate phase space from d σ X+n, and from accept/reject/ reweighting/unweighting steps Scheme |M X+2 | 2 Scale hierarchies: smaller single-scale phase-space region … Powers of alphaS pile up “Fake Sudakovs” from Better Starting Point: a QCD fractal? Clusterings or Pseudoshowers d σ X+n from Reweightings or Subtractions 3 P. S k a n d s
Matrix-Element Matching Standard Paradigm: Double counting, IR divergences, multiscale logs Have ME for X, X+1,…, X+n; Want to combine and add showers → “The Soft Stuff” Works pretty well at low multiplicities Still, only corrected for “hard” scales; Soft still pure LL. 4 P. S k a n d s
Matrix-Element Matching Standard Paradigm: Double counting, IR divergences, multiscale logs Have ME for X, X+1,…, X+n; Want to combine and add showers → “The Soft Stuff” Works pretty well at low multiplicities Still, only corrected for “hard” scales; Soft still pure LL. At high multiplicities: Efficiency problems: slowdown from need to compute and generate phase space from d σ X+n , and from unweighting Scale hierarchies: smaller single-scale phase-space region Powers of alphaS pile up 4 P. S k a n d s
Matrix-Element Matching Standard Paradigm: Double counting, IR divergences, multiscale logs Have ME for X, X+1,…, X+n; Want to combine and add showers → “The Soft Stuff” Works pretty well at low multiplicities Still, only corrected for “hard” scales; Soft still pure LL. At high multiplicities: Efficiency problems: slowdown from need to compute and generate phase space from d σ X+n , and from unweighting Scale hierarchies: smaller single-scale phase-space region Powers of alphaS pile up Better Starting Point: a QCD fractal? 4 P. S k a n d s
Matrix-Element Corrections Interleaved Paradigm: Have shower; want to improve it using ME for X, X+1, …, X+n. 5 P. S k a n d s
Matrix-Element Corrections Interleaved Paradigm: Have shower; want to improve it using ME for X, X+1, …, X+n. Interpret all-orders shower structure as a trial distribution Quasi-scale-invariant : intrinsically multi-scale (resums logs) Unitary : automatically unweighted (& IR divergences → multiplicities) More precise expressions imprinted via veto algorithm: ME corrections at LO, NLO, and more? → soft and hard No additional phase-space generator or σ X+n calculations → fast 5 P. S k a n d s
Matrix-Element Corrections Interleaved Paradigm: Interleaved Paradigm: Have shower; want to improve it using ME for X, X+1, …, X+n. Have shower; want to improve it using ME for X, X+1, …, X+n. Interpret all-orders shower structure as a trial Interpret all-orders shower structure as a trial distribution distribution Quasi-scale-invariant : intrinsically multi-scale (resums logs) Quasi-scale-invariant : intrinsically multi-scale (resums logs) Unitary : automatically unweighted (& IR divergences → multiplicities) Unitary : automatically unweighted (& IR divergences → multiplicities) More precise expressions imprinted via veto algorithm: ME More precise expressions imprinted via veto algorithm: ME corrections at LO, NLO, and more? → soft and hard corrections at LO, NLO, and more? → soft and hard No additional phase-space generator or σ X+n calculations → fast No additional phase-space generator or σ X+n calculations → fast Existing Approaches: Existing Approaches: First Order: PYTHIA and POWHEG First Order: PYTHIA and POWHEG Beyond First Order: PYTHIA → too complicated. POWHEG → very Beyond First Order: PYTHIA → too complicated. POWHEG → very active, still mostly in framework of standard paradigm. GENEVA? active, still mostly in framework of standard paradigm. GENEVA? 5 P. S k a n d s
Markov is Crucial LO: Giele, Kosower, Skands, PRD 84 (2011) 054003 NLO: Hartgring, Laenen, Skands, arXiv:1303.4974 Problems: Traditional parton showers are history-dependent (non-Markovian) → Number of generated terms (possible clustering histories) grows like 2 N N! + Complicated kinematics Parton- (or Catani-Seymour) Shower: After 2 branchings: 8 terms + Dead zones After 3 branchings: 48 terms After 4 branchings: 384 terms Solutions: Markovian Evolution, Matched Antenna Showers, and Smooth Ordering No need to ever cluster back more than one step → Number of generated terms grows like N + Simple expansions + Dead zones merely suppressed 6 P. S k a n d s
Markov is Crucial LO: Giele, Kosower, Skands, PRD 84 (2011) 054003 NLO: Hartgring, Laenen, Skands, arXiv:1303.4974 Problems: Traditional parton showers are history-dependent (non-Markovian) → Number of generated terms (possible clustering histories) grows like 2 N N! + Complicated kinematics Parton- (or Catani-Seymour) Shower: After 2 branchings: 8 terms + Dead zones After 3 branchings: 48 terms After 4 branchings: 384 terms Solutions: Markovian Evolution, Matched Antenna Showers, and Smooth Ordering No need to ever cluster back more than one step → Number of generated terms grows like N + Simple expansions + Dead zones merely suppressed 6 P. S k a n d s
Markov is Crucial LO: Giele, Kosower, Skands, PRD 84 (2011) 054003 NLO: Hartgring, Laenen, Skands, arXiv:1303.4974 Problems: Traditional parton showers are history-dependent (non-Markovian) → Number of generated terms (possible clustering histories) grows like 2 N N! + Complicated kinematics Parton- (or Catani-Seymour) Shower: After 2 branchings: 8 terms + Dead zones After 3 branchings: 48 terms After 4 branchings: 384 terms Solutions: Markovian Evolution, Matched Antenna Showers, and Smooth Ordering No need to ever cluster back more than one step → Number of generated terms grows like N + Simple expansions Markovian Antenna Shower: After 2 branchings: 2 terms + Dead zones merely suppressed After 3 branchings: 3 terms After 4 branchings: 4 terms 7 P. S k a n d s
Recommend
More recommend