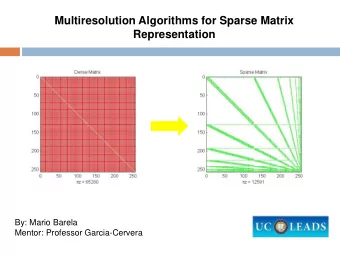
Multiresolution Matrix Factorization Risi Kondor, The University of - PowerPoint PPT Presentation

Multiresolution Matrix Factorization Risi Kondor, The University of Chicago Nedelina Teneva Pramod Mudrakarta UChicago UChicago

. Wavelets on graphs • Learning on graphs • Semi-supervised learning [Shuman et al., 2013]] 2 / 32 2/32 .

. Wavelets on graphs: recent work • Diffusion Wavelets [Coifman & Maggioni, 2006] • Treelets [Lee, Nadler & Wasserman, 2008] • Spectral graph wavelets [Hammond, Vandergheynst & Gribonval, 2010] • Tree wavelets [Gavish, Nadler & Coifman, 2010] • Laplacian eignevector based wavelets [Irion & Saito, 2015] 3 / 32 3/32 .

. Fast multilevel Wavelets on graphs ← → matrix algorithms 4 / 32 4/32 .

Multiresolution analysis

. Fourier to Wavelets − → • Canonical (eigenfunctions of • Generated from some mother translation operator / Laplacian). wavelet by translations and dilations. • Perfectly localized in frequency. • Localized in space and frequency. • Perfectly delocalized in position. • Much better at resolving discontinuities. 6 / 32 6/32 .

. Multiresolution on R : wavelets 1. Define the mother wavelet ψ . 2. Define the basis m ( x ) = 2 − ℓ/ 2 ψ (2 − ℓ x − m ) ψ ℓ 3. The wavelet transform of a function f is f ( x ) = ∑ m ( x ) + ∑ ℓ,m α ℓ m ψ ℓ m β m φ m ( x ) 7 / 32 7/32 .

. More abstractly... Repeatedly split the space of functions on X into the direct sum of a { } φ ℓ • Scaling space V ℓ +1 (with basis ) m { } ψ ℓ • Wavelet space W ℓ +1 (with basis ). m The key to fast wavelet transforms is the that each orthogonal map V ℓ �→ V ℓ +1 ⊕ W ℓ +1 is a very sparse. 8 / 32 8/32 .

. Multiresolution on R Mallat [1989] showed (roughly) that if 1. ∩ j V ℓ = { 0 } , 2. ∪ ℓ V ℓ is dense in L 2 ( R ) , 3. If f ∈ V ℓ then f ′ ( x ) = f ( x − 2 ℓ m ) is also in V ℓ for any m ∈ Z , 4. If f ∈ V ℓ , then f ′ ( x ) = f (2 x ) is in V ℓ − 1 , then there is a mother wavelet ψ and a father wavelet φ s. t. m = 2 − ℓ/ 2 ψ (2 − ℓ x − m ) m = 2 − ℓ/ 2 φ (2 − ℓ x − m ) . ψ ℓ φ ℓ and 9 / 32 9/32 .

. Multiresolution on discrete spaces Which of the ideas from classical multiresolution still make sense? • Repeatedly split L ( X ) into smoother and rougher parts. ✓ • Basis functions should be localized in space & frequency. ✓ Q ℓ • Each Φ ℓ → Φ ℓ +1 ∪ Ψ ℓ +1 transform is orthogonal and sparse. ✓ − m is derived by translating ψ ℓ → MAYBE • Each ψ ℓ • Each ψ ℓ is derived by scaling ψ → ??? 10 / 32 10/32 .

. General principles 1. The sequence L ( X ) = V 0 ⊃ V 1 ⊃ V 2 ⊃ . . . is a filtration of R n in terms of smoothness with respect to T in the sense that µ ℓ = f ∈ V ℓ \{ 0 } ⟨ f, Tf ⟩ / ⟨ f, f ⟩ inf increases at a given rate. 2. The wavelets are localized in the sense that ψ ℓ m ( y ) x ∈ X sup inf d ( x, y ) α y ∈ X increases no faster than a certain rate. 3. Letting Q ℓ be the matrix expressing Φ ℓ ∪ Ψ ℓ in the previous basis Φ ℓ − 1 , i.e., m = ∑ dim( V ℓ − 1 ) φ ℓ [ Q ℓ ] m,i φ ℓ − 1 i =1 i m = ∑ dim( V ℓ − 1 ) ψ ℓ [ Q ℓ ] m +dim( V ℓ − 1 ) ,i φ ℓ − 1 , i =1 i each Q ℓ orthogonal transform is sparse, guaranteeing the existence of a fast wavelet transform ( Φ 0 is taken to be the standard basis, φ 0 m = e m ). 11 / 32 11/32 .

Multiresolution Matrix Factorization (MMF)

. Classical approach: Define wavelets − → Derive FWT MMF approach: Prescribe form of FWT − → Wavelets fall out 13 / 32 13/32 .

. Multiresolution Matrix Factorization ( . ( . ( . . ( . ( . ( . ) ) ) ) ) ) . . . . . . ≈ Q ⊤ Q ⊤ Q L Q 1 A H 1 L • Each Q ℓ is super-sparse (Givens rotation or k –point rotation). • For some nested sequence of sets [ n ] = S 1 ⊇ S 2 ⊇ . . . ⊇ S L +1 , [ Q ℓ ] [ n ] \ S ℓ , [ n ] \ S ℓ = I n − δ ℓ − 1 . • H is core-diagonal. Here A can be the Laplacian of a graph or any symmetric matrix . 14 / 32 14/32 .

. Multiresolution Matrix Factorization ( . . ( . ( . ( . ( . ( . ) ) ) ) ) ) ≈ . . . . . . Q ⊤ Q ⊤ A H Q L Q 1 1 L The columns of Q ⊤ 1 Q ⊤ 2 . . . Q ⊤ L are a • Wavelet basis for the column space of A . • A multilevel sparse dictionary (hierarchically sparse PCA). MMF structure is a generalization of the notion of rank. 15 / 32 15/32 .

. Computation MMF reduces find the wavelet basis to an optimization problem ∥ A − Q ⊤ 1 . . . Q ⊤ L H Q L . . . Q 1 ∥ 2 minimize Frob . [ n ] ⊇ S 1 ⊇ . . . ⊇ S L H ∈H n S L ; Q 1 , . . . , Q L ∈ Q for a given class Q of local rotations and dimensions δ 1 ≥ δ 2 ≥ . . . δ L . Natural greedy optimization approach: A �→ Q 1 AQ ⊤ 1 �→ Q 2 Q 1 AQ ⊤ 1 Q ⊤ 2 �→ . . . . In practice combined with randomization and othe tricks to make it fast. 16 / 32 16/32 .

. Hierarchical structure The sequence in which MMF (with k ≥ 3 ) eliminates dimensions induces a (soft) hierarchical clustering amongst the dimensions (mixture of trees). 17 / 32 17/32 .

. Applications 1. Generate a wavelet bass for graphs/matrices. 2. Reveal structural properties of graphs (communities). 3. Generate graphs with hierarchical structure. 4. Compress graphs and matrices (sketching). 5. Fast approximate matrix inverse → preconditioner. 6. Hierachical scaffold for other fast numerics. 18 / 32 18/32 .

. Relationship to other algorithms • Treelets [Lee, Nadler & Wasserman, 2008]: special case with k = 2 and heuristic approach. • Diffusion wavelets [Coifman and Maggioni, 2006]: fual approach – focus on smoothness rather than sparsity (leads to repeated Gram–Schmidt). • Fast multipole methods [Greengard & Rokhlin, 1987–] Aggregate at different scales. • Multigrid [Brandt, 1970s–] Solve complex problems at multiple scales that communicate with each other. • Hierarchical Matrices [Hackbusch, Borm, Chandrasekaran,…] H –matrices, H 2 –matrices, HSS matrices,... 19 / 32 19/32 .

The pMMF library

. http://people.cs.uchicago.edu/ risi/MMF/index.html Highly optimized open source parallel C++ library: • Custom sparse matrix classes • Blocked matrices → parallelism • Randomization, etc.. • Interface: C++ API/Matlab/command line/GUI. 21 / 32 21/32 .

. Blocking and stages Rows/columns are clustered, matrix is correspondingly blocked, and rotations are found within clusters. A run of rotations conforming to the same clustering structure is called a stage . �→ · · . . . . � �� � � �� � � �� � � �� � A A Q ⊤ Q ⊤ 1 1 Different columns of blocks (“towers”) can be sent to different processors. 22 / 32 22/32 .

. Reblocking After the stage is complete, rows/columns are reclustered. It is critical that reblocking also be efficient. �→ �→ �→ . . . . . . . . . . . �→ �→ . . . 23 / 32 23/32 .

. Matrix Free Arithmetic When applying an MMF factorization to a vector, the vector must go through the same reblocking process. . . . . . . . � �� � � �� � � �� � ���� v Q 3 Q 2 Q 1 24 / 32 24/32 .

. Graph demo 25 / 32 25/32 .

. Compression results 26 / 32 26/32 .

. Preconditioning results 27 / 32 27/32 .

. Wall clock time 28 / 32 28/32 .

. Further Applications [Meneveau] [Lieberman-Aiden et al., 2009] 29 / 32 29/32 .

CONCLUSIONS

. Conclusions • Matrices coming from data are usually NOT like ◦ Random matrices ◦ Worst case matrices ◦ Low rank matrices. • Large–scale problems can only be solved by breaking them into smaller ones. ◦ In Applied Math there is a long tradition of this, but not obvious how to translate it to less structured setting. ◦ MMF is a way to find the multiresolution structure in data and exploit it for both computational and statistical ends. • Multiresolution structure is an alternative to the notion of rank. 31 / 32 31/32 .

. Acknowledgements Co-authors: • Nedelina Teneva (UChicago) • Pramod Mudrakarta (UChicago) • Vikas Garg (MIT) Thanks: • Andreas Krause and Joel Tropp. 32 / 32 32/32 .