Multiresolution Algorithms for Sparse Matrix Representation By: - PowerPoint PPT Presentation

Multiresolution Algorithms for Sparse Matrix Representation By: Mario Barela Mentor: Professor Garcia-Cervera

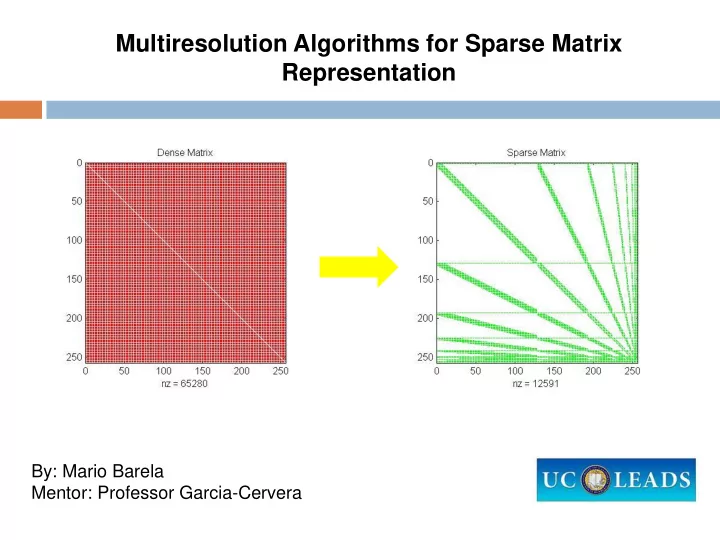
Big Picture What is it all about ? 1 4 3 7 8 6  Dense Matrix 2 5 9 0 4 0 0 0 0  Sparse Matrix 0 0 9 Importance?  Efficiency  Faster Solutions Applications?  Sciences ACM SIGGRAPH 1995 Conference  Systems of equations Proceedings , 173-182  Image Processing  Data Analysis

Research Project Goals Questions:  What algorithms can effectively transform a given dense matrix into a sparse one?  Will the new representation accurately model the original to a certain degree of error?

Research Project Goals Project Goals: Learn Algorithms : Modify Algorithms : Run Large Scale Simulations A B

Experimental Methods for Multiresolution Algorithm 1 2 3 • Remove odd • Evaluate at odd • Repeat process. data points. data points. • Obtain coarser • Interpolate • Subtract odd resolution then between even data points and truncate to data points. store. achieve compression. K+3 K+2 K+1 Differences } K 0 1 2 3 4 5 6 7 8

1-D Data Compression 1200 Nonzeros 1000 800 Original tol=.001 600 tol=.01 tol=.1 400 200 0 A(x) B(x) C(x)

Experimental Data

Multiresolution and Standard Form 𝐷𝑝𝑛𝑞𝑠𝑓𝑡𝑡𝑗𝑝𝑜 𝐵 𝑁𝑆 𝐷𝑖𝑏𝑜𝑕𝑓 𝑝𝑔 𝐶𝑏𝑡𝑓 𝐵 𝑇 𝐵 Given an 𝑂𝑦𝑂 matrix 𝐵, and an 𝑂𝑦1 vector 𝑔, we compute 𝐵𝑔 as follows: (𝐵𝑔) 𝑁𝑆 = 𝐵 𝑇 𝑔 𝑁𝑆

Standard Form Data 70000 Matrix A: 256x256 NONZEROS 60000 50000 40000 tol=10 ⁻⁴ tol=10 ⁻⁷ 30000 20000 10000 0 2-point Linear 3-point Parabolic 4-point Cubic 6-point

Matrix-Vector Multiplication ((𝑗 − 𝑘) 2 ); 𝑗𝑔 𝑗 ≠ 𝑘,  𝐵 𝑗, 𝑘 = log 0 𝑓𝑚𝑡𝑓𝑥ℎ𝑓𝑠𝑓 𝑔 𝑗 = sin 2𝜌 𝑗 𝑂 Product (𝐵𝑔) Error ∙ ∞ -error = 4.35 ∗ 10 −2

Results and Conclusions Results :  𝐵 𝐵 𝑁𝑆 𝐵 𝑇  The order of interpolation used effected the sparsity of transformed matrices and accuracy of multiplication.  Achieved similar results to that of Shalom who used six point- interpolation. Future Plans:  Test the efficiency of our Algorithms in respect to matrix-vector multiplication.  Use our multiresolution algorithms to efficiently solve problems that arise in Mathematics and the Sciences.

Results and Conclusions Acknowledgements:  Professor Carlos Garcia-Cervera: Department of Mathematics, University of California Santa Barbara.  University of California Leadership Excellence through Advanced Degrees (UC LEADS). References:  Ami Harten and Itai Yad- Shalom “Fast Multiresolution Algorithms for Matrix- Vector Multiplication”.  [1] Francesc Arandiga and Vicente F. Candela “ Multiresolution Standard Form of a Matrix”.