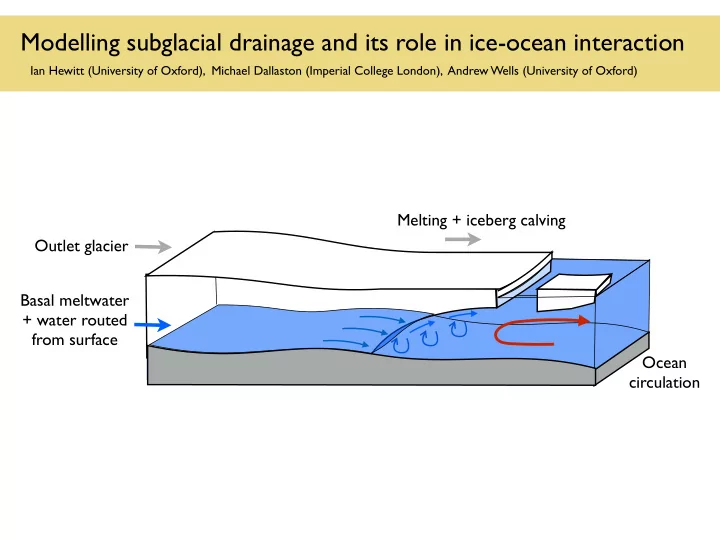

Modelling subglacial drainage and its role in ice-ocean interaction Ian Hewitt (University of Oxford), Michael Dallaston (Imperial College London), Andrew Wells (University of Oxford) Melting + iceberg calving Outlet glacier Basal meltwater + water routed from surface Ocean circulation
I. What do models tell us about how subglacial discharge is delivered at grounding lines? II. How does the spatial distribution of subglacial discharge affect the shape of ice shelves?
Subglacial drainage Permeable sediments ‘Distributed’ systems ‘Channel’ systems
Channel dynamics Hydraulic potential / �r � = ⇢ w gZ b + p w Z s Discharge (turbulent flow) − 1 / 2 @� � � @� Q Q = − K c S 4 / 3 � � Z b � � @ s @ s � � Cross-sectional area Ice creep M − 2 A ∂ S ∂ t = ρ w S Melting n n S | N | n − 1 N N = p i − p w ρ i ⇤ ⇤ - Most of the potential energy dissipated by turbulence is converted to latent heat M = − 1 − ⇢ w c � Q @� @ s − ⇢ w gc � Q @ Z b ⇢ w L L @ s Röthlisberger 1972, Nye 1976
Channel dynamics Steady-state channel with constant discharge Z s Z = � / ⇢ w g p Z b S U = Q/S - Melting rate and creep closure rate are reduced near grounding line. - Results in trumpet-like shape of channels, and relatively low water speed at outlet.
Channel dynamics Steady-state channel with constant discharge Z s Z = � / ⇢ w g p Z b With advection S U = Q/S - However, advection of channels with the ice prevents them becoming too large ∂ S M � 2 A ∂ t + u b · r S = ρ w n n SN n ρ i C ⇡ 3 m 1 / 4 s � 27 / 44 - Further analysis indicates outflow water speed U ⇡ CQ 2 / 11 u 9 / 44 (sin ✓ ) 9 / 44 b
General comments - Routing of subglacial water controlled primarily by topography (probably largest factor in determining portal locations). - Expect large seasonal signal of subglacial discharge when surface meltwater present. - Subglacial drainage system exhibits instabilities that likely lead to episodic discharge (in addition to weather-driven episodes).
I. What do models tell us about how subglacial discharge is delivered at grounding lines? II. How does the spatial distribution of subglacial discharge affect the shape of ice shelves?
Previous modelling results Melt rate Channel depth Petermann ice shelf b c 35 35 N 60 200 ice shelf z 30 30 active ocean y 50 layer x τ 0 25 25 150 − τ 0 40 stagnant ambient layer z = s ( x, y, t ) 20 20 600m z = b ( x, y, t ) v 0 30 100 15 15 z = a ( x, y, t ) inflow boundary 20 10 10 40 km 50 20 km 10 5 5 0 0 0 5 10 15 5 10 15 Across-shelf distance (km) Across-shelf distance (km) Gladish et al 2012 Melt rate (a) Plume thickness Sergienko 2013 (c)
A simplified model - ice z y ∝ x u h z = b ( x, y, t ) m D U S T m T T a S a e Q g Depth-integrated model for ice shelf (standard) Parameterised interface melting ∂ h mL = c γ T | U | ( T � T m ) . ∂ t + r · ( h u ) = � ( ρ o / ρ i ) m, ✓ ◆� ✓ ∂ u ◆� ∂ 2 ∂ u ∂ x + ∂ v + ∂ ∂ y + ∂ v � (1 � ρ i / ρ o ) ρ i gh ∂ h 2 η h η h ∂ x = 0 , ∂ x ∂ y ∂ y ∂ x ✓ ∂ u ∂ y + ∂ v ◆� ✓ ∂ u ∂ x + 2 ∂ v ◆� � (1 � ρ i / ρ o ) ρ i gh ∂ h ∂ + ∂ η h 2 η h ∂ y = 0 , ∂ x ∂ x ∂ y ∂ y + prescribed ice depth and speed over grounding line
A simplified model - plume z y ∝ x u h z = b ( x, y, t ) m D U S T m T T a S a e Q g Simplified plume model (conservation laws) Parameterised entraiment e = E 0 | U || ⌅ b | , Along slope buoyancy due to salinity r · ( D U ) = e + m, ✓ ∂ b (coupling to ice dynamics) ◆ ∂ x � ∂ D r · ( D U U ) = Dg β S S ∆ + r · ( κ D r U ) � C d | U | U ∂ x ✓ ∂ b ◆ ∂ y � ∂ D r · ( D U V ) = Dg β S S ∆ + r · ( κ D r V ) � C d | U | V ∂ y r · ( D U S ) = eS a + r · ( κ D r S ) + mS i , Turbulent eddy viscosity r · ( D U T ) = eT a + r · ( κ D r T ) + mT m � mL (smooths small-scale velocity differences) c . Heat exchange with ice + prescribed subglacial discharge at grounding line
Reduced model results One-dimensional steady-state ice-shelf shape (melting rate approximately uniform) surface s 0 base b Larger subglacial discharge − 1 0 0 . 2 0 . 4 0 . 6 0 . 8 1 1 . 2 1 . 4 1 . 6 1 . 8 2 x Linear stability analysis - Small transverse perturbation of arbitrary wavenumber (due to variable grounding-line ice depth or variable subglacial discharge) (b) y ˜ h ( x ) ˜ h g
Reduced model results Ice depth perturbation Amplitude of perturbation X/ 2) unreg. δ = 0 ( ν = 0) δ = 0 . 036 10 2 ν = 0 . 002 10 1 10 0 ν = 0 . 02 ice 10 − 1 50 100 150 k Wave number of perturbation (d) - Perturbations at grounding line grow downstream, driven by transverse flow into channels and enhanced buoyancy-driven acceleration. - Transverse ice flow is relatively ineffective at smoothing out channels. - Stabilisation of small wavelengths is due to turbulent mixing in the plume layer. Dallaston, Hewitt & Wells, in review
Summary Subglacial drainage channels are likely to trumpet out near grounding line. Expect a smooth transition from subglacial melting (potential energy) to frontal melting (ocean heat). Uneven spatial distribution of discharge and/or basal topography at grounding line can cause channelisation due to enhanced melting of the shelf. Primary factors in channelisation are flow-focussing and buoyancy-driven acceleration, counteracted by turbulent mixing.
Recommend
More recommend