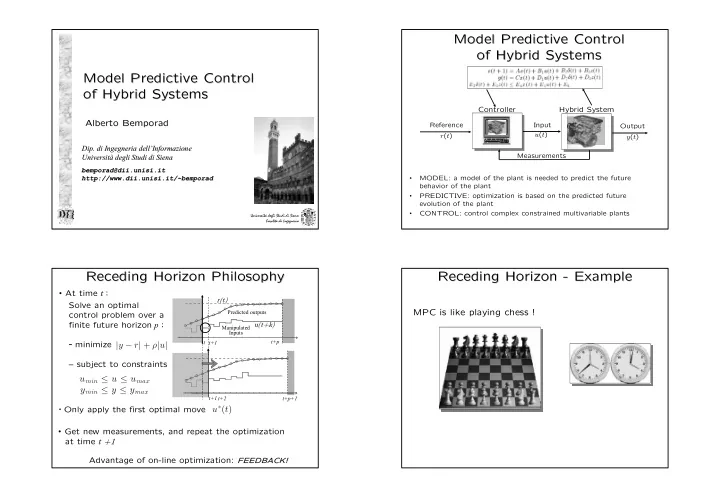

Model Predictive Control Model Predictive Control of Hybrid Systems of Hybrid Systems Model Predictive Control Model Predictive Control of Hybrid Systems of Hybrid Systems Controller Hybrid System Alberto Bemporad Alberto Bemporad Reference Input Output u ( t ) r ( t ) y ( t ) Dip. di Ingegneria Dip. di Ingegneria dell’Informazione dell’Informazione Università degli degli Studi Studi di Siena di Siena Measurements Università bemporad@dii.unisi.it bemporad@dii.unisi.it • http://www.dii.unisi.it/~bemporad http:// www.dii.unisi.it/~bemporad MODEL: a model of the plant is needed to predict the future behavior of the plant • PREDICTIVE: optimization is based on the predicted future evolution of the plant • CONTROL: control complex constrained multivariable plants Università degli Studi di Siena Facoltà di Ingegneria Receding Horizon Philosophy Receding Horizon - - Example Example Receding Horizon Philosophy Receding Horizon • At time t : r(t) Solve an optimal Predicted outputs MPC is like playing chess ! control problem over a finite future horizon p : u(t+k) Manipulated Inputs – minimize t+p t t+1 | y à r | + ú | u | – subject to constraints u min ô u ô u max y min ô y ô y max t+1 t+2 t+p+1 • Only apply the first optimal move u ã ( t ) • Get new measurements, and repeat the optimization at time t +1 Advantage of on-line optimization: FEED FEEDBAC BACK!
MPC for Hybrid Systems Closed- -Loop Stability Loop Stability MPC for Hybrid Systems Closed past future Model Predicted y(t+k|t) outputs Predictive (MPC) Manipulated Control Inputs u(t+k) t+T t t+1 • At time t solve with respect to the finite-horizon open-loop, optimal control problem: (Bemporad, Morari 1999) • Apply only (discard the remaining optimal inputs) u ( t ) = u ã ( t ) Proof: Easily follows from standard Lyapunov arguments • Repeat the whole optimization at time t +1 Stability Proof Hybrid MPC - - Example Example Stability Proof Hybrid MPC Switching System: " # ô õ cos ë ( t ) à sin ë ( t ) 0 x ( t + 1) = 0 . 8 x ( t ) + u ( t ) sin ë ( t ) cos ë ( t ) 1 y ( t ) = 0 1 ] x ( t ) Closed loop: [ Lyapunov function ù if [1 0] x ( t ) õ 0 y ( t ) , r ( t ) u ( t ) 3 ë ( t ) = ù if [1 0] x ( t ) < 0 à 3 Constraint: à 1 ô u ( t ) ô 1 time t time t Open loop: Note: Glob Global opt optimum not imum not ne needed for convergence ! eded for convergence !
MIQP Formulation of MPC MIQP Formulation of MPC (Bemporad, Morari, 1999) Optimal Control of Hybrid Systems: Optimal Control of Hybrid Systems: Computational Aspects Computational Aspects Mixed Integer Quadratic Program (MIQP) MILP Formulation of MPC Formulation of MPC MILP Mixed- -Integer Program Solvers Integer Program Solvers Mixed (Bemporad, Borrelli, Morari, 2000) 4000 4000 Cost of Computation • Mixed-Integer Programming is NP-hard 50 var 40 var 3000 3000 20 var Phase transitions have been found in 2000 2000 computationally hard problems. 1000 1000 BUT 0 2 • Introduce slack variables: min ï 2 3 3 4 4 5 5 6 6 7 7 8 min | x | Ratio of Constraints to Variables s . t . ï õ x (Monasson et al., Nature , 1999) ï õ à x • General purpose Branch & Bound/Branch & Cut solvers available ï x õ [ Qy ( t + k | t )] i i = 1 , . . . , p, k = 1 , . . . , T à 1 k for MILP and MIQP (CPLEX, Xpress-MP, BARON, GLPK, ...) ï x õ k Qy ( t + k | t ) k ∞ ï x à [ Qy ( t + k | t )] i i = 1 , . . . , p, k = 1 , . . . , T à 1 õ k k ï u õ k Ru ( t + k ) k ∞ ï u More solvers and benchmarks: http://plato.la.asu.edu/bench.html õ [ Ru ( t + k ))] i i = 1 , . . . , m, k = 0 , . . . , T à 1 k k ï u õ à [ Ru ( t + k ))] i i = 1 , . . . , m, k = 0 , . . . , T à 1 k • No need to reach global optimum (see proof of the theorem), although performance deteriorates • Set ø , [ ï x 1 , . . . , ï x N y , ï u 1 , . . . , ï T à 1 , U, î, z ] T à 1 X ï x i + ï u J ( ø, x ( t )) = Good for large sampling times (e.g., 1 h) / expensive hardware … min i ø Mixed Integer Linear Program k =0 … but not for fast sampling (e.g. 10 ms) / cheap hardware ! s . t .Gø ô W + Sx ( t ) (MILP)
On- -Line vs. Off Line vs. Off- -Line Optimization Line Optimization On min U J ( U, x ( t )) , P T à 1 k Qy ( t + k + 1 | t ) k ∞ + k Ru ( t + k ) k ∞ k =0 MLD model subj . to x ( t | t ) = x ( t ) x ( t + T | t ) = 0 Explicit Form of Explicit Form of Model Predictive Control Model Predictive Control • On-line optimization: given x ( t ), solve the problem at each time step t Mixed-Integer Linear Program (MILP) via Multiparametric Multiparametric Programming Programming via • Off-line optimization: solve the MILP fo for a r all x ( t ) J ( ø, x ( t )) , f 0 ø min ø s . t .Gø ô W + Fx ( t ) multi-parametric Mixed Integer Linear Program (mp-MILP) Linear MPC Linear MPC Example of Multiparametric Multiparametric Solution Solution Example of • Linear Model: ø ∈ R 2 Multiparametric LP ( ) CR { 1 , 4 } CR { 1 , 2 , 3 } 60 40 CR { 1 , 3 } 20 • Constraints: CR { 2 , 3 } 0 x 2 - 2 0 • Optimal control problem (quadratic performance index): - 4 0 - 6 0 - 6 0 - 4 0 - 2 0 0 20 40 60 x 1
Linear MPC Linear MPC Multiparametric Multiparametric Quadratic Programming Quadratic Programming (Bemporad et al., 2002) • Substitution: • Optimization problem: (quadratic) (linear) Convex vex Q QUADR ADRATIC TIC PRO PROGRA RAM M (QP) P) • Objective: solve the QP for for a all • Assumption: (always satisfied if QP problem originates from optimal control problem) Linearity of the Solution Determining a Critical Region Linearity of the Solution Determining a Critical Region x 0 ∈ X solve QP to find • Impose primal and dual feasibility: identify active constraints at linear inequalities in x ! form matrices by collecting active constraints • Remove redundant constraints KKT • critical region CR 0 x 0 optimality conditions: CR 0 CR 0 = {A x ô B} From (1) : x -space From (2) : X • à , W à , S à CR 0 is the set of all and only parameters x for which G is the optimal combination of active constraints at the optimizer In some neighborhood of x 0 , λ and U are explicit affine functions of x !
Multiparametric QP QP Multiparametric QP QP Multiparametric Multiparametric R 2 R 2 CR 0 = {A x ô B} CR 0 = {A x ô B} R 3 R 3 • • x 0 x 0 R 1 R 1 R i = { x ∈ X : A i x > B i , A j z ô B j , ∀ j < i } R i = { x ∈ X : A i x > B i , A j z ô B j , ∀ j < i } CR 0 CR 0 R N R 4 R N R 4 { CR 0 , R 1 , . . . , R N } { CR 0 , R 1 , . . . , R N } x -space x -space Theore The rem: Theore The rem: X ò R n X ò R n is a partition of is a partition of X X R i Proceed iteratively: for each region Note: while is characterizing a set of active constraints, is not CR 0 R i repeat the whole procedure with X ← R i X The recursive algorithm terminates after a finite X number of steps, because the number of combinations Keep track of the CR already of active constraints is finite explored, don ’ t split CRs QP – – More efficient method Mp- -QP QP Properties Properties Mp Mp- -QP More efficient method Mp (Tøndel, Johansen, Bemporad, 2003) x 2 x 2 x 2 CR CR CR continuous, piecewise affine x 1 x 1 x 1 convex, continuous, The active set of a neighboring region is found by using piecewise quadratic, C 1 (if no degeneracy) the active set of the current region + knowledge of the type of hyperplane we are crossing: Corol Corollary: The linear MPC controller is a continuous piecewise affine function of the state ⇒ The corresponding constraint is adde dded to the active set ⇒ The corresponding constraint is withdr hdrawn from the active set
Complexity Reduction Double Integrator Example Complexity Reduction Double Integrator Example ô õ ô õ 1 u ( t ) 1 1 0 2.5 2.5 CR1 x ( t + 1) = x ( t ) + u ( t ) CR1 y ( t ) = s 2 • System: CR2 CR2 0 1 1 2 CR3 2 CR3 CR4 CR4 CR5 CR5 1.5 CR6 1.5 CR6 CR7 sampl mpling + Z ng + ZOH y ( t ) = 1 [ 0 ] x ( t ) CR7 CR8 1 CR9 1 T s =1 =1 s 0.5 0.5 • Constraints: 0 à 1 ô u ( t ) ô 1 0 -0.5 -0.5 -1 -1 P ∞ y 0 ( t ) y ( t ) + 100 1 u 2 ( t ) • Control objective: minimize -1.5 -1.5 t =0 -2 -2 u t + k = K LQ x ( t + k | t ) ∀ k õ N u -2.5 -2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5 -2.5 -2.5 -2 -1.5 -1 -0.5 0 0.5 1 1.5 2 2.5 • Optimization problem: for N u =2 (cost function is normalized by max λ (H)) Regions where the first component of the solution is the same can be joined (when their union is convex). (Bemporad, Fukuda, Torrisi, Computational Geometry , 2001) mp- -QP solution QP solution Complexity mp Complexity N u =4 N u =5 N u =3 N u =2 40 N u =6 CPU time 20 0 0 5 10 15 20 300 # Regions 200 100 0 0 5 10 15 20 # free moves
Recommend
More recommend