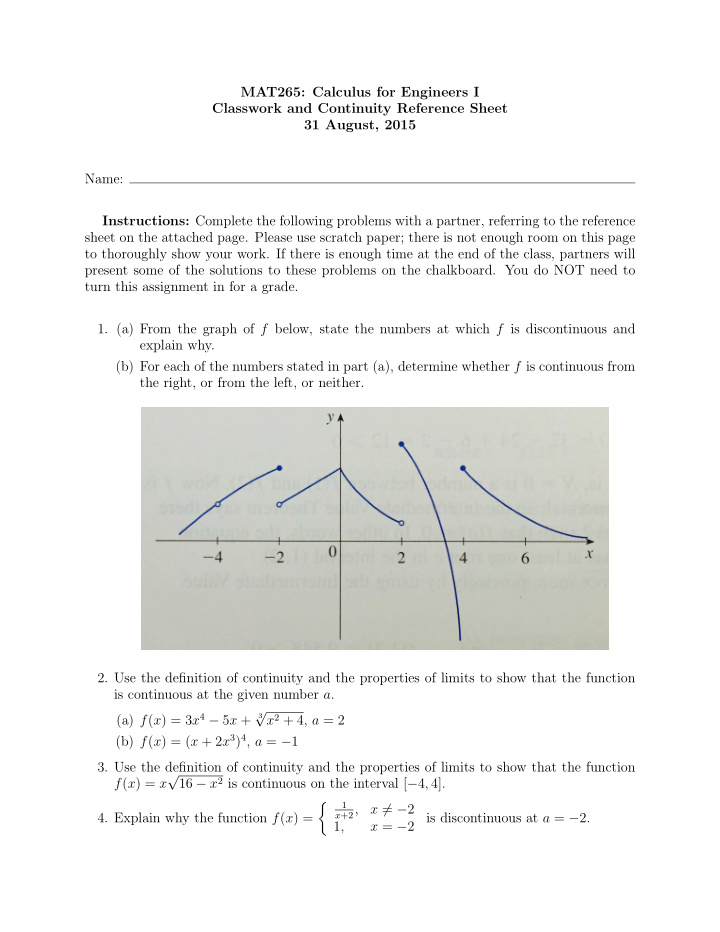
MAT265: Calculus for Engineers I Classwork and Continuity Reference - PDF document

MAT265: Calculus for Engineers I Classwork and Continuity Reference Sheet 31 August, 2015 Name: Instructions: Complete the following problems with a partner, referring to the reference sheet on the attached page. Please use scratch paper; there is not enough room on this page to thoroughly show your work. If there is enough time at the end of the class, partners will present some of the solutions to these problems on the chalkboard. You do NOT need to turn this assignment in for a grade. 1. (a) From the graph of f below, state the numbers at which f is discontinuous and explain why. (b) For each of the numbers stated in part (a), determine whether f is continuous from the right, or from the left, or neither. 2. Use the definition of continuity and the properties of limits to show that the function is continuous at the given number a . √ (a) f ( x ) = 3 x 4 − 5 x + x 2 + 4, a = 2 3 (b) f ( x ) = ( x + 2 x 3 ) 4 , a = − 1 3. Use the definition of continuity and the properties of limits to show that the function √ 16 − x 2 is continuous on the interval [ − 4 , 4]. f ( x ) = x � 1 x +2 , x � = − 2 4. Explain why the function f ( x ) = is discontinuous at a = − 2. 1 , x = − 2

5. Use continuity to evaluate the limit. 5 + √ x (a) lim x → 4 √ 5 + x (b) lim x → π sin( x + sin x ) 6. For what value of the constant c is the function f continuous on ( −∞ , ∞ )? cx 2 + 2 x, � x < 2 f ( x ) = x 3 − cx x ≥ 2 . 7. Find the values of a and b that make the function f continuous everywhere. x 2 − 4  x − 2 , x < 2   f ( x ) = ax 2 − bx + 3 , 2 ≤ x < 3   2 x − a + b, x ≥ 3 . 8. The following functions have removable discontinuities at the given value of a . Find a function g that agrees with f for x � = a and is continuous at a . (a) f ( x ) = x 4 − 1 x − 1 , a = 1 (b) f ( x ) = x 3 − x 2 − 2 x , a = 2 x − 2

The following information can be found in Section 1.5 of your textbook. Definition: A function f is continuous at a number a if lim x → a f ( x ) = f ( a ) . If f is not continuous at a , we say that f is discontinuous at a . Definition: A function f is continuous from the right at a number a if x → a + f ( x ) = f ( a ) lim and f is continuous from the left at a if x → a − f ( x ) = f ( a ) . lim Definition: A function f is continuous on an interval if it is continuous at every number in the interval. (If f is defined only on one side of an endpoint of the interval, we understand continuous at the endpoint to mean continuous from the right or continuous from the left . Theorem: If f and g are continuous at a and c is a constant, then the following functions are also continuous at a : 1. f + g 2. f − g 3. cf 4. fg 5. f/g , provided g ( a ) � = 0. Theorem: If f is continuous at b and lim x → a g ( x ) = b , then lim x → a f ( g ( x )) = f ( b ). In other words, � � x → a f ( g ( x )) = f lim x → a g ( x ) lim . Theorem: If g is continuous at a and f is continuous at g ( a ), then the composite function f ◦ g given by ( f ◦ g )( x ) = f ( g ( x )) is continuous at a . Theorem: The following types of functions are continuous at every number in their domains: polynomials, rational functions, root functions, and trigonometric functions.