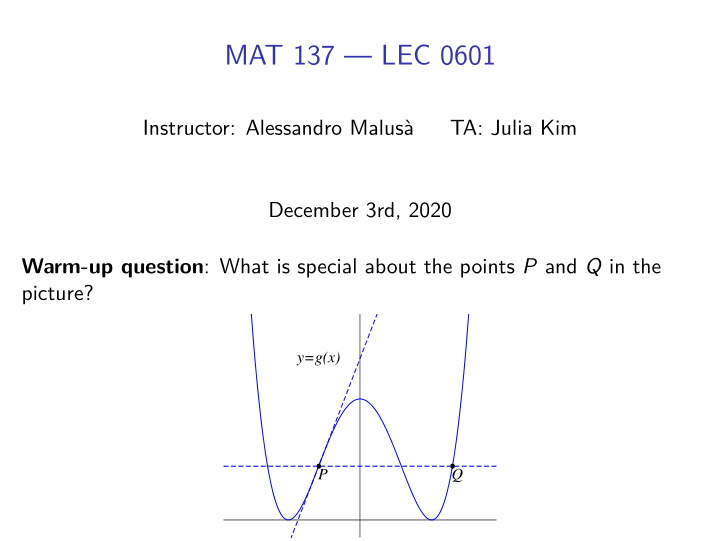
MAT 137 LEC 0601 Instructor: Alessandro Malus TA: Julia Kim - PowerPoint PPT Presentation

MAT 137 — LEC 0601 Instructor: Alessandro Malusà TA: Julia Kim December 3rd, 2020 Warm-up question : What is special about the points P and Q in the picture? y=g(x) P Q

Find the coordinates of P and Q g ( x ) = x 4 − 6 x 2 + 9 y=g(x) P Q

True or False – Concavity and inflection points Let f be a differentiable function with domain R . Let c ∈ R . Let I be an interval. Which implications are true? 1 IF f is concave up on I , THEN ∀ x ∈ I , f ′′ ( x ) > 0. 2 IF ∀ x ∈ I , f ′′ ( x ) > 0, THEN f is concave up on I . THEN f ′ is increasing on I . 3 IF f is concave up on I 4 IF f ′ is increasing on I , THEN f is concave up on I . 5 IF f has an I.P. at c , THEN f ′′ ( c ) = 0. 6 IF f ′′ ( c ) = 0, THEN f has an I.P. at c . THEN f ′ has a local extremum at c 7 IF f has an I.P. at c , 8 IF f ′ has a local extremum at c , THEN f has an I.P. at c . I.P. = “inflection point"

A polynomial from 3 points Construct a polynomial that satisfies the following three properties at once: 1 It has an inflection point at x = 2 2 It has a a local extremum at x = 1 3 It has y -intercept at y = 1.

Before next class... • Watch videos 6.6, 6.7, and 6.8, and then 6.9 and 6.5. • Download the next class’s slides (no need to look at them!)