M ETABOLIC P ETRI N ETS M ONIKA H EINER , properties properties - PowerPoint PPT Presentation
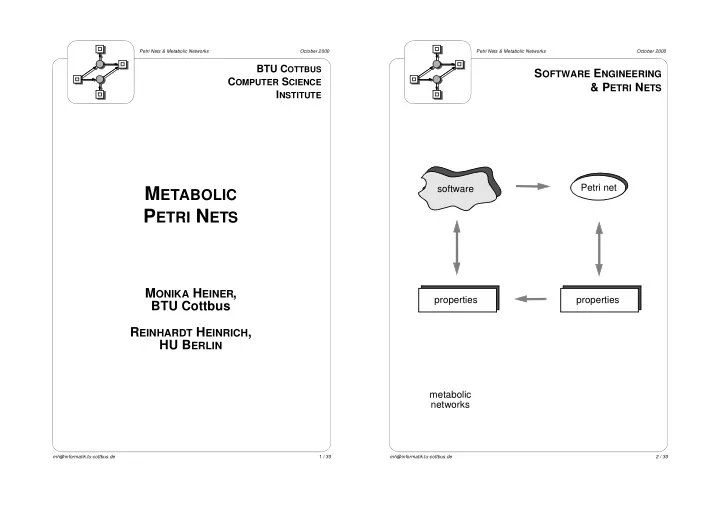
Petri Nets & Metabolic Networks October 2000 Petri Nets & Metabolic Networks October 2000 BTU C OTTBUS S OFTWARE E NGINEERING C OMPUTER S CIENCE & P ETRI N ETS I NSTITUTE Problem Petrinetz Petri net software M ETABOLIC P ETRI N
Petri Nets & Metabolic Networks October 2000 Petri Nets & Metabolic Networks October 2000 BTU C OTTBUS S OFTWARE E NGINEERING C OMPUTER S CIENCE & P ETRI N ETS I NSTITUTE Problem Petrinetz Petri net software M ETABOLIC P ETRI N ETS M ONIKA H EINER , properties properties BTU Cottbus R EINHARDT H EINRICH , HU B ERLIN metabolic networks mh@informatik.tu-cottbus.de 1 / 30 mh@informatik.tu-cottbus.de 2 / 30
Petri Nets & Metabolic Networks October 2000 Petri Nets & Metabolic Networks October 2000 T OOL O VERVIEW informal specification press hierarchical hierarchy PED Petri Net Editor browser with output filters arm 2 functional PEDVisor testing protocols arm 1 (distributed) animation tool (rapid prototyping) elevating rotary table deposit belt (belt 2) functional requirements safety robot requirements qualitative INA PEP PROD SMV analysis protocols qualitative Petri net analyzers Production Cell: travelling crane performance feed belt (belt 1) requirements quantitative TimeNet INA analysis protocols (stochastic) (non-stochastic) quantitative Petri net analyzers execution FUNLite motion protocols lib execution tool mh@informatik.tu-cottbus.de 3 / 30 mh@informatik.tu-cottbus.de 4 / 30
Petri Nets & Metabolic Networks October 2000 Petri Nets & Metabolic Networks October 2000 E XAMPLE NAD + P ENTOSE P HOSPHATE C YCLE NADH P i + 1,3-BPG GAP 15 glucose 6-phosphate ADP 14 fructose ribose 16 6-phosphate 13 5-phosphate 8 ATP fructose 1,6-bisphosphate 2 NADP + 3PG 2 NADPH DHAP glucose ribulose 12 6-phosphate 5-phosphate 17 dihydroxyacetone glycerinaldehyde CO 2 E4P F6P phosphate 3-phosphate ribose 5-phosphate FBP 2PG 1. possibility 2. possibility 7 ADP 18 2 NADP + 2 NADPH S7P GAP 11 glucose ribulose PEP 6-phosphate 5-phosphate ATP F6P CO 2 ADP 6 Xu5P ribose fructose 5-phosphate R5P 6-phosphate Qualitative Analysis of Biochemical Reaction Systems; 19 Reddy, V. N.; Liebman, M. N.; Mavrovouniotis, M. L.: 2 NADP + Computers in Biology and Medicine 26(96), 9-24. fructose ATP 2 NADPH 10 1,6-bisphosphate 5 4 glucose ribulose Pyr 6-phosphate 5-phosphate Ru5P NADH G6P CO 2 dihydroxyacetone glycerinaldehyde fructose ribose phosphate 3-phosphate 3 6-phosphate 5-phosphate ADP 20 2 NADPH 2 NADP + 3. possibility NAD + fructose 1,6-biphosphate 9 ATP Lac Gluc dihydroxyacetone glycerinaldehyde 2 [R EDDY 96] phosphate 3-phosphate E XAMPLE 2 ATP 2 GSSG 4 GSH pyruvate Stryer, L.: [Reddy 96] Biochemistry; 4. possibility Freeman, New York, NY, 1995, p. 450. 1 mh@informatik.tu-cottbus.de 5 / 30 mh@informatik.tu-cottbus.de 6 / 30
Petri Nets & Metabolic Networks October 2000 Petri Nets & Metabolic Networks October 2000 P ETRI N ETS , P ETRI N ETS , B ASICS 1 B ASICS 2 (3) TOKENS (1) NODES (moving objects, places transitions vehicles, work pieces, dates, control flow pointer, ..., units of substances (e. g. Mol) , ...) condition is not fulfilled “passive elements” “active elements” conditions events condition is (one times) fulfilled states actions “ chem. compounds ” “ chem. reactions ” n condition is n times fulfilled (2) ARCS postconditions preconditions (4) MARKING (system state, substance distribution ) 5 How many tokens are on each place? 3 event -> initial marking mh@informatik.tu-cottbus.de 7 / 30 mh@informatik.tu-cottbus.de 8 / 30
Petri Nets & Metabolic Networks October 2000 Petri Nets & Metabolic Networks October 2000 P ETRI N ETS , E XAMPLES , B ASICS 3 R EACTION E QUATIONS (5) FLOW OF TOKENS ❑ FOR LIGHT - INDUCED PHOSPHORYLATION 2 NAD + + 2 H 2 O -> 2 NADH + 2 H + + O 2 ❑ an event may happen, if -> all preconditions NADH are fulfilled NAD + 2 2 (corresponding to the arc weights); 2 H + ❑ if an event happens, then r1 2 H 2 O O 2 -> tokens are removed from all preconditions (corresponding to the arc weights), and ❑ FROM THE PHOTOSYNTHESIS -> tokens are added 2 CO 2 + H 2 S + 2 H 2 O -> 2 (CH 2 O) + H 2 SO 4 to all postconditions (corresponding to the arc weights); CO 2 ❑ an event happens CH 2 O 2 2 (firing of a transition) H 2 S -> atomic r2 2 H 2 SO 4 -> time-less H 2 O mh@informatik.tu-cottbus.de 9 / 30 mh@informatik.tu-cottbus.de 10 / 30
Petri Nets & Metabolic Networks October 2000 Petri Nets & Metabolic Networks October 2000 T YPICAL M ETABOLIC B ASIC P ETRI N ETS S TRUCTURES (1) PLACES ❑ CHAIN OF REACTIONS -> involved substances / chem. compounds r2 MB3 MB1 r1 MB2 ❑ substrates (boundary places), ❑ ( FREE - CHOICE ) BRANCHING r2 OutSub InSub r1 input substrat output substrat MB2 r1 MB1 e. g. glucose, lactate; MB3 r2 ❑ metabolites, e. g. glucose 6-phosphate ❑ BRANCHING WITH SIDE CONDITION ❑ side conditions for reactions, e. g. electron carrier, phosphate carrier; MB2 r1 ❑ enzymes, if any MB1 MB3 r2 mh@informatik.tu-cottbus.de 11 / 30 mh@informatik.tu-cottbus.de 12 / 30
Petri Nets & Metabolic Networks October 2000 Petri Nets & Metabolic Networks October 2000 M ETABOLIC M ETABOLIC P ETRI N ETS 2 P ETRI N ETS 3 (2) TRANSITIONS (3) ARC INSCRIPTIONS ❑ spontaneous reactions -> amount of the units of substances involved in the reaction ❑ enzyme-catalyzed reactions, two ways of modelling: (4) AMOUNT OF TOKENS without the enzyme concentration -> amount of available units of substances MB1 MB2 Enzym (5) INITIAL MARKING with the enzyme concentration x enzyme -> initial substance distribution x x enzym-catalyzed MB1 MB2 reaction Σ M ETABOLIC P ETRI N ET ( M P N ): x - amount of units of substances required by the reaction set of all paths from the input to the output substrates ❑ transport steps, if any taking into consideration the -> inhomogeneous substance distribution; stoichiometric relations; mh@informatik.tu-cottbus.de 13 / 30 mh@informatik.tu-cottbus.de 14 / 30
Petri Nets & Metabolic Networks October 2000 Petri Nets & Metabolic Networks October 2000 E XAMPLE E XAMPLE [R EDDY 96] [R EDDY 96] AS P ETRI N ET , AS P ETRI N ET , V ERSION 1 V ERSION 2 Gluc ATP ADP Ru5P G6P NADP+ Xu5P S7P E4P 2 2 NADPH Ru5P Xu5P GSSG R5P NADPH GSSG F6P 2 GSH ATP GAP 2 F6P 2 R5P ADP S7P GAP FBP 2 2 2 E4P F6P GSH NADP+ GAP DHAP NAD+ DHAP Pi ATP ADP ATP ADP NADH 1,3-BPG ADP GAP ATP G6P Gluc F6P FBP NAD+ 3PG Pi 2PG NAD+ NADH ATP ADP ATP ADP NADH PEP ADP 2PG 1,3-BPG ATP Lac Pyr PEP 3PG Pyr NADH NAD+ glukose1.ped glukose2.ped Lac mh@informatik.tu-cottbus.de 15 / 30 mh@informatik.tu-cottbus.de 16 / 30
Petri Nets & Metabolic Networks October 2000 Petri Nets & Metabolic Networks October 2000 E XAMPLE E XAMPLE [R EDDY 96] [R EDDY 96] AS P ETRI N ET , AS P ETRI N ET , V ERSION 3 V ERSION 4 Gluc Gluc ATP ATP ADP ADP Ru5P Ru5P G6P G6P NADP+ NADP+ 2 2 2 2 NADPH NADPH Xu5P Xu5P GSSG R5P GSSG R5P F6P F6P 2 2 GSH GSH ATP ATP 2 2 ADP ADP GAP S7P GAP S7P FBP FBP F6P F6P E4P E4P GAP GAP NAD+ NAD+ DHAP DHAP 1,3-BPG 1,3-BPG Pi Pi ADP ADP NADH NADH 1,3-BPG 1,3-BPG ATP ATP 3PG 3PG ADP ADP 2 2 ATP ATP two-layered representation reduced to NADH NADH 2PG 2PG NAD+ NAD+ Lac Lac PEP PEP ADP ADP ATP ATP Pyr Pyr NADH NADH NAD+ NAD+ glukose3.ped glukose4.ped Lac Lac mh@informatik.tu-cottbus.de 17 / 30 mh@informatik.tu-cottbus.de 18 / 30
Petri Nets & Metabolic Networks October 2000 Petri Nets & Metabolic Networks October 2000 T YPICAL E XAMPLE P ETRI N ET [R EDDY 96] Q UESTIONS AS P ETRI N ET , V ERSION 5 Gluc b2 b1 (1) How many tokens may reside at most in a ATP given place? ADP Ru5P G6P a2 NADP+ 2 2 2 a1 ❑ (0, 1, k, oo) 3 b1 NADPH a2 b2 2 -> BOUNDEDNESS a1 3 Xu5P R5P GSSG F6P 2 GSH ATP 2 ADP S7P GAP (2) How often may a transition fire? FBP ❑ (0-times, n-times, oo-times) F6P E4P GAP -> LIVENESS NAD+ DHAP Pi NADH (3) Is a given system state 1,3-BPG ADP 2 ❑ always reachable again? 4 7 ATP Lac Gluc 2 -> PROGRESS PROPERTIES start NADH 7 7 7 NAD+ ❑ never reachable? ATP ADP Pi -> SAFETY PROPERTIES Lac glukose4_zyk.ped mh@informatik.tu-cottbus.de 19 / 30 mh@informatik.tu-cottbus.de 20 / 30
Petri Nets & Metabolic Networks October 2000 Petri Nets & Metabolic Networks October 2000 A SSUMPTIONS T YPICAL IN V ERSION 5 A NALYSIS T ECHNIQUES 1 (1) TOKEN GAME (?) ❑ the two appearances of GAP can be separated (2) REACHABILITY GRAPH (no logical / fusion nodes) nodes: system states arcs: the firing transition z1 ❑ the branching probabilities t4 at the conflicts of t2 t1 G6P and Ru5P z2 z3 are known and may be characterized by the relations t3 G6P - 3 : 1 z4 Ru5P - 2 : 1 -> STEADY STATE : (3) REDUCED REACHABILITY GRAPH all intermediates have to be balanced with respect to inputs and outputs (4) STRUCTURAL ANALYSES e. g.: conservative -> bounded mh@informatik.tu-cottbus.de 21 / 30 mh@informatik.tu-cottbus.de 22 / 30
Recommend
More recommend
Explore More Topics
Stay informed with curated content and fresh updates.