Logic? Propositional Logic, Truth Tables (Rosen, Sections 1.1, 1.2, - PowerPoint PPT Presentation

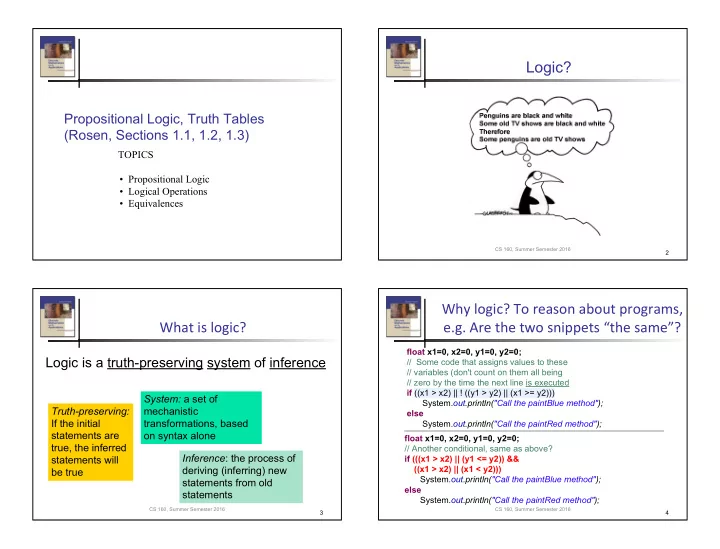
Logic? Propositional Logic, Truth Tables (Rosen, Sections 1.1, 1.2, 1.3) TOPICS • Propositional Logic • Logical Operations • Equivalences CS 160, Summer Semester 2016 2 Why logic? To reason about programs, What is logic? e.g. Are the two snippets “the same”? float x1=0, x2=0, y1=0, y2=0; Logic is a truth-preserving system of inference // Some code that assigns values to these // variables (don't count on them all being // zero by the time the next line is executed if ((x1 > x2) || ! ((y1 > y2) || (x1 >= y2))) System: a set of System. out.println("Call the paintBlue method"); Truth-preserving: mechanistic else If the initial transformations, based System. out.println("Call the paintRed method"); statements are on syntax alone float x1=0, x2=0, y1=0, y2=0; true, the inferred // Another conditional, same as above? Inference : the process of statements will if (((x1 > x2) || (y1 <= y2)) && deriving (inferring) new ((x1 > x2) || (x1 < y2))) be true System. out.println("Call the paintBlue method"); statements from old else statements System. out.println("Call the paintRed method"); CS 160, Summer Semester 2016 CS 160, Summer Semester 2016 3 4

What are the options to answer Are the two snippets “the same”? Let’s build towards the math Options: ■ We want to reason about Boolean expressions A: They are both the same (we’re not guessing ■ They are built out of numbers (and also strings) and can come by after class and show you) and variables and operators B: They are both different (we’re not guessing ■ Operators as functions: and can come by after class and show you) ■ The comparison operator > maps two numbers to a C: We have no clue but want to figure this out Boolean value: D: We will write the program, run it for many So do all comparison/relational operators values and report back to you ■ Boolean operators ( || , &&)? They map two Booleans E: This is not an interesting problem ■ to a Boolean value: CS 160, Summer Semester 2016 CS 160, Summer Semester 2016 5 6 Only Boolean variables/operators inside the condition Towards the math: let’s simplify float x1=0, x2=0, y1=0, y2=0; ■ If we reason over all possible numeric values boolean b1,b2,b3,b4,b5; life will be hard (and it will take a long time). // Replace // if ((x1 > x2) || ! ((y1 > y2) || (x1 >= y2))) ■ For now, focus only on Boolean expressions: // by b1 = (x1 > x2); b2 = (y1 > y2); b3 = (x1 >= y2); variables ■ if (b1 || ! (b2 || b3)) values ■ // and in the other one expressions built using Boolean operators ■ // replace ■ How? // if (((x1 > x2) || (y1 <= y2)) && // ((x1 > x2) || (x1 < y2))) Let’s modify the program ■ // by b4 = (y1 <= y2); b5= (x1 < y2); if ((b1 || b4) && (b1 || b5)) CS 160, Summer Semester 2016 CS 160, Summer Semester 2016 7 8

Welcome to Propositional Logic Propositional Logic ■ Also known as: ■ A proposition is a statement that is either true or false ■ Propositional calculus ■ Examples: ■ Boolean algebra ■ This class is CS160 (true) ■ Propositional logic allows us to prove or disprove equalities that appear in programs: ■ Today is Sunday (false) ■ For example, is (b1 || !(b2 || b3)) the same ■ It is currently raining in Singapore (???) thing as (b1 || !b2) || (b1 || !b3)) ? ■ The value may be unknown (i.e., a variable) ■ Yes, they are (always) equivalent by ■ Similar to numerical expressions, propositional De Morgan’s Law and Distributive Law. logic also defines operators. CS 160, Summer Semester 2016 CS 160, Summer Semester 2016 9 10 Propositional Logic (II) Truth Tables ■ The truth value of a compound ■ A propositional statement is one of: propositional statement is determined by ■ A simple proposition ■ denoted by a capital letter, e.g. ‘A’. its truth table ■ A negation of a propositional statement ■ Truth tables define the truth value of a ■ e.g. ¬ A : “not A” connective for every possible truth value of ■ Two propositional statements joined by an operator ■ e.g. A ∧ B : “A and B” its terms ■ e.g. A ∨ B : “A or B” ■ Use parentheses as needed (precedence is a convention) ■ e.g. A ∧ (B ∨ C) CS 160, Summer Semester 2016 CS 160, Summer Semester 2016 11 12

Logical negation Negation Truth Table ■ Negation of proposition A is ¬ A ¬ A A A: It is snowing. 0 1 ■ ¬ A: It is not snowing ■ 1 0 A: Newton knew Einstein. ■ ¬ A: Newton did not know Einstein. ■ A: I am not registered for CS195. ■ ¬ A: I am registered for CS195. ■ CS 160, Summer Semester 2016 CS 160, Summer Semester 2016 13 14 Truth Table for Conjunction Logical and ( conjunction ) ■ Conjunction of A and B is A ∧ B A ∧ B A B A: CS160 teaches logic. ■ 0 0 0 B: CS160 teaches Java. ■ A ∧ B: CS160 teaches logic and Java. ■ 0 1 0 1 0 0 ■ Combining conjunction and negation 1 1 1 A: I like fish. ■ B: I like sushi. ■ I like fish but not sushi: A ∧ ¬ B ■ CS 160, Summer Semester 2016 CS160 - Spring Semester 2016 15 16

Logical or ( disjunction ) Truth Table for Disjunction ■ Disjunction of A and B is A ∨ B A ∨ B A B A: Today is Friday. ■ 0 0 0 B: It is snowing. ■ A ∨ B: Today is Friday or it is snowing. ■ 0 1 1 1 0 1 ■ This statement is true if any of the following hold: 1 1 1 Today is Friday ■ It is snowing ■ Both ■ Otherwise it is false ■ CS 160, Summer Semester 2016 CS 160, Summer Semester 2016 17 18 Confusion over Inclusive OR and Exclusive OR Exclusive Or ■ The “or” connective ∨ is inclusive: it is true ■ Restaurants typically let you pick one (either if either or both arguments are true soup or salad, not both) when they say “The ■ There is also an exclusive or ⊕ entrée comes with a soup or salad”. A ⊕ B ■ Use exclusive OR to write as a logic proposition A B ■ Give two interpretations of the sentence using 0 0 0 inclusive OR and exclusive OR: 0 1 1 ■ Students who have taken calculus or intro to 1 0 1 programming can take this class 1 1 0 CS 160, Summer Semester 2016 CS 160, Summer Semester 2016 19 20

Conditional & Biconditional Implication Conditional implication ■ The conditional implication connective is → ■ A: A programming homework is due. ■ The biconditional implication connective is ↔ ■ B: It is Tuesday. ■ A → B: ■ These, too, are defined by truth tables ■ If a programming homework is due, then it must be Tuesday. A → B A ↔ B A B A B ■ A programming homework is due only if it is Tuesday. ■ Is this the same? 0 0 1 0 0 1 ■ If it is Tuesday, then a programming homework is 0 1 1 0 1 0 due. 1 0 0 1 0 0 1 1 1 1 1 1 CS 160, Summer Semester 2016 21 CS160 - Spring Semester 2016 22 Bi-conditional Compound Truth Tables ■ Truth tables can also be used to determine ■ A: You can drive a car. the truth values of compound statements, ■ B: You have a driver’s license. such as (A ∨ B) ∧ ( ¬ A) (fill this as an exercise) ■ A ↔ B ■ You can drive a car if and only if you have a A ∨ B (A฀B)฀(฀A) ¬ A A B driver’s license (and vice versa). 0 0 1 0 0 ■ What if we said “if”? ■ What if we said “only if”? 0 1 1 1 1 1 0 0 1 0 1 1 0 1 0 CS 160, Summer Semester 2016 CS 160, Summer Semester 2016 23 24

Tautology and Contradiction Examples ■ A tautology is a compound proposition that is always true. A ∨ ¬A A ∧ ¬A A ¬A ■ A contradiction is a compound proposition that 0 1 1 0 is always false. ■ A contingency is neither a tautology nor a 1 0 1 0 contradiction. Result is always ■ A compound proposition is satisfiable if there is false, no matter at least one assignment of truth values to the what A is Result is always variables that makes the statement true. true, no matter Therefore, it is a what A is Therefore, it is a contradiction tautology CS 160, Summer Semester 2016 CS 160, Summer Semester 2016 25 26 Prove ¬(p ∧ q) ≡ ¬p ∨ ¬q Logical Equivalence ■ Two compound propositions, p and q , are p p q q ¬p ∨ ¬q logically equivalent if p ↔ q is a tautology. ¬p ¬q (p ∧ q) ¬(p ∧ q) ■ Notation: p ≡ q 0 0 1 1 0 1 1 ■ De Morgan’s Laws: 0 1 1 0 0 1 1 ■ ¬ (p ∧ q) ≡ ¬ p ∨ ¬ q ■ ¬ (p ∨ q) ≡ ¬ p ∧ ¬ q 1 0 0 1 0 1 1 ■ How so? Let’s build a truth table! 1 1 0 0 1 0 0 = CS 160, Summer Semester 2016 CS 160, Summer Semester 2016 27 28

Show ¬(p ∨ q) ≡ ¬p ∧ ¬q Other Equivalences ■ Show p → q ≡ ¬p ∨ q p p q q ¬q (p ∨ q) ¬(p ∨ q) ¬p ¬p ∧ ¬q 0 0 1 1 0 1 1 ■ Show Distributive Law: 0 1 1 0 1 0 0 ■ p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r) 1 0 0 1 1 0 0 1 1 0 0 1 0 0 = CS 160, Summer Semester 2016 CS 160, Summer Semester 2016 29 30 Show p → q ≡ ¬p ∨ q Show p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r) q ∧ r p ∨ q p ∨ r p ∨ (q ∧ r) (p ∨ q) ∧ (p ∨ r) p q r p q ¬p p → q ¬p ∨ q 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 0 0 0 1 1 1 0 1 0 0 1 0 0 0 0 1 1 1 1 0 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 0 0 0 0 1 0 1 0 1 1 1 1 1 1 0 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 = CS 160, Summer Semester 2016 = 31 CS 160, Summer Semester 2016 32