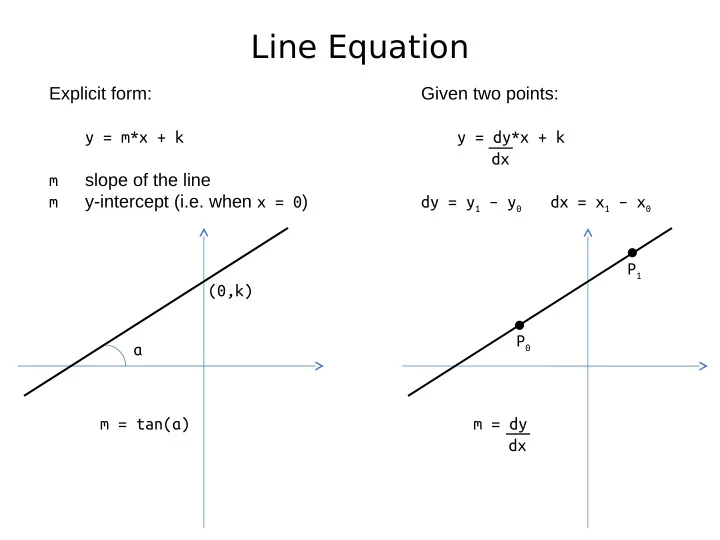
Line Equation Explicit form: Given two points: y = m*x + k y = - PowerPoint PPT Presentation

Line Equation Explicit form: Given two points: y = m*x + k y = dy*x + k dx m slope of the line m y-intercept (i.e. when x = 0 ) dy = y 1 – y 0 dx = x 1 – x 0 P 1 (0,k) P 0 α m = tan(α) m = dy dx

Lines and Slopes m = 0 m = ∞ m = +1 m = -1 (α = 0) (α = 90) (α = 45) (α = -45) m = (-∞..-1) m = (-1..0) m = (0..1) m = (1..∞) (α = -90..45) (α = -45..0) (α = 0..45) (α = 45..90)

Line Drawing (Naïve) Given two points P 0 (x 0 ,y 0 ) and P 1 (x 1 ,y 1 ) : 1. find the line equation y = m*x + k 2. for each x in [x 0 , x 1 ] : calculate y and plot (x, y) Assumptions: x 0 <= x 1 m = [-1..1] def drawLine(x0, y0, x1, y1): compute m and k for each x in [x0 , x1]: y = m*y + k plot(x, round(y))

Line Drawing (Incremental) Given a line equation y = m*x + k knowing the coordinates of P(x,y) makes it easy to calculate y’ for the neighbor point P’(x+1,y’) y’ = m*x’ + k = m*(x + 1) + k = m*x + m + k = m*x + k + m = y + m So to get the next y , just add the slope to the current y value def drawLine(x0, y0, x1, y1): compute the slope m start at y = y0 for each x in [x0 , x1]: plot(x, round(y)) y = y + m

Line Equation Implicit form: If we let: a*x + b*y + c = 0 F(x, y) = a*x + b*y + c the line is all points (x,y) then that satisfy the equation F(x, y) = 0 (x,y) on the line F(x, y) < 0 (x,y) “below” the line F(x, y) > 0 (x,y) “above” the line

Line Equation Implicit form: If we let: a*x + b*y + c = 0 F(x, y) = a*x + b*y + c the line is all points (x,y) then that satisfy the equation F(x, y) = 0 (x,y) on the line F(x, y) < 0 (x,y) “below” the line F(x, y) > 0 (x,y) “above” the line F(P) = a*x + b*y + c = 0 P” F(P”) = ? P P' F(P’) = ?

Line Equation Implicit form: If we let: a*x + b*y + c = 0 F(x, y) = a*x + b*y + c the line is all points (x,y) then that satisfy the equation F(x, y) = 0 (x,y) on the line F(x, y) < 0 (x,y) “below” the line F(x, y) > 0 (x,y) “above” the line F(P) = a*x + b*y + c = 0 P” F(P”) = F(x, y+1) = a*x + b*(y+1) + c = P = a*x + b*y + b + c = = a*x + b*y + c + b = P' = F(P) + b = b F(P’) = F(x, y-1) = -b

Line Drawing (Midpoint) Pick the pixel closest to the line P” d” d’ P’ Expensive, since it requires distance computation

Line Drawing (Midpoint) Instead of calculating the true distances d’ and d” (time consuming) check on which side of the line the midpoint M lies, i.e. check whether F(M) > 0 or F(M) < 0 P” d” M d’ P’ Pick P’ if M above the line, i.e. F(M) > 0 Pick P” if M is below the line, i.e. F(M) < 0

Line Drawing (Midpoint) Midpoint lets us decide (1) which vertex to pick (2) which midpoint to consider next M NE ? M M E ? should we highlight vertex below M and move left to examine M E OR should we highlight vertex above midpoint and move diagonally to examine M NE

Line Drawing (Midpoint) Midpoint lets us decide (1) which vertex to pick (2) which midpoint to consider next ? ? M M M E ? ?

Line Drawing (Midpoint) Midpoint lets us decide (1) which vertex to pick (2) which midpoint to consider next ? M NE ? ? M M ?

Line Drawing (Midpoint) Midpoint lets us decide (1) which vertex to pick (2) which midpoint to consider next ? ? M M M E ? ? ? M NE ? ? M M ?

Line Drawing (Midpoint) Given two points P 0 (x 0 ,y 0 ) and P 1 (x 1 ,y 1 ) pick the closest pixels to the line. Assumptions: x 0 < x 1 m = [0..1] Start with the implicit equation a*x + b*y + c = 0 where a = dy , b = -dx , c = k*dx Use the idea from the incremental algorithm: if we know the value at F(M) can we calculate efficiently F(M E ) or F(M NE ) M NE M M E

Line Drawing (Midpoint) Calculating the value F(M E ) Coordinates: M(x, y) M E (x+1,y) F(M E ) = a*(x+1) + b*y + c = a*x + a + b*y + c = a*x + b*y + c + a = F(M) + a M M E Calculating the value F(M NE ) Coordinates: M(x, y) M NE (x+1,y+1) F(M NE ) = a*(x+1) + b*(y+1) + c = a*x + a + b*y + b + c M NE = a*x + b*y + c + a + b = F(M) + a + b M

Line Drawing (Midpoint) Calculating the value F(M 0 ) Coordinates: P 0 (x 0 ,y 0 ) M 0 (x 0 +1,y 0 +½) F(M 0 ) = a*(x 0 +1) + b*(y 0 +½) + c = a*x 0 + a + b*y 0 + b/2 + c = a*x 0 + b*y 0 + c + a + b/2 M 0 = F(P 0 ) + a + b/2 = 0 + a + b/2 P 0 = a + b/2

Line Drawing (Midpoint) In summary, if M i “above” the line, i.e. go E F(M i+1 ) = F(M i ) + a F(M i+1 ) = F(M i ) + (a+b) if M i “below” the line, i.e. go NE for the first midpoint M 0 F(M 0 ) = a + b/2 To avoid the division in the term b/2 we could go back and use: F(x, y) = 2a*x + 2b*y + 2c same line as F(x, y) = a*x + b*y + c Finally, if M i “above” the line, i.e. go E F(M i+1 ) = F(M i ) + 2a F(M i+1 ) = F(M i ) + 2(a+b) if M i “below” the line, i.e. go NE for the first midpoint M 0 F(M 0 ) = 2a + b

Line Drawing (Issues) Endpoint order: The assumption was that x 1 < x 2 i.e. drawing from “left” to “right” If x 1 > x 2 i.e. drawing from “right” to “left” could simply swap P 1 and P 2 However, swapping will not work if the lines have styles, since it will lead to discontinuities in the pattern.

Line Drawing (Issues) Endpoint order: The assumption was that x 1 < x 2 i.e. drawing from “left” to “right” If x 1 > x 2 i.e. drawing from “right” to “left” could simply swap P 1 and P 2 Challenges: if lines have styles, swapping P 1 and P 2 will lead to discontinuities in the pattern

Line Drawing (Issues) Starting at the edge of a clip rectangle: P 2 P 1 x min x max

Line Drawing (Issues) Starting at the edge of a clip rectangle: P 2 P' 1 P 1 x min x max instead of drawLine(P 1 ,P 2 ) compute P' 1 = ( x min, m*x min + k) and drawLine(P' 1 ,P 2 ) however, the two lines will have different slopes and will be drawn differently

Line Drawing (Issues) Starting at the edge of a clip rectangle: P 2 M P' 1 M 0 P 1 x min x max to fix, plot P' 1 = ( x min, m*x min + k) but also set M 0 to closest midpoint to start algo

Line Drawing (Issues) Starting at the edge of a clip rectangle: y max P 2 y min P 1

Line Drawing (Issues) Starting at the edge of a clip rectangle: y max P 2 y min P' 1 P 1 instead of drawLine(P 1 ,P 2 ) compute P' 1 = (( y min -k)/m,x min ) and drawLine(P' 1 ,P 2 ) however, the two lines will have different slopes and will be drawn differently

Line Drawing (Issues) Starting at the edge of a clip rectangle: y max y min Y min - ½ may miss a pixel – adjust the clip window

Line Drawing (Issues) Starting at the edge of a clip rectangle: y min Y min - ½ M

Line Drawing (Issues) Varying intensity with respect to slope: same number of pixels to represent different lengths