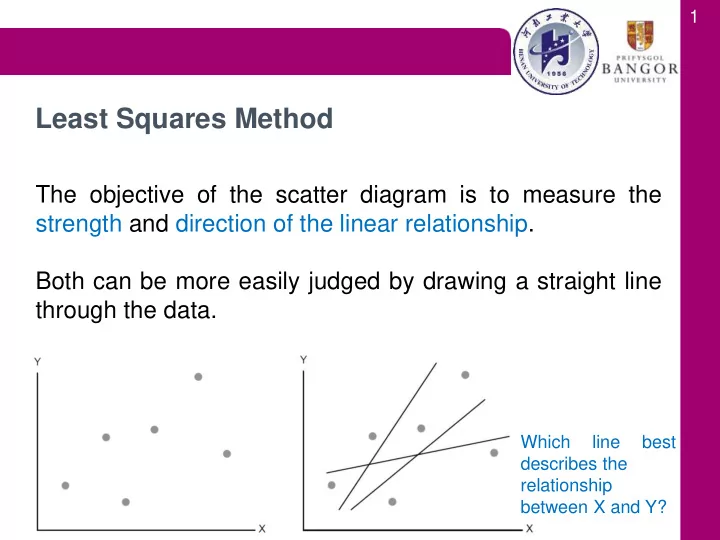

1 Least Squares Method The objective of the scatter diagram is to measure the strength and direction of the linear relationship. Both can be more easily judged by drawing a straight line through the data. Which line best describes the relationship between X and Y?
2 Least Squares Method We need an objective method of producing a straight line. The best line will be one that is “closest” to the points on the scatterplot. In other words, the best line is one that minimises the total distance between itself and all the observed data points. Since we oftentimes use regression to predict values of Y from observed values of X, we choose to measure the distance vertically.
3 Least Squares Method We want to find the line that minimises the vertical distance between itself and the observed points on the scatterplot. So here we have 2 different lines that may describe the relationship between X and Y. To determine which one is best, we can find the vertical distances from each point to the line... So based on this, the line on the right is better than the line on the left in describing the relationship between X and Y. ***infinite number of lines***
4 Least Squares Method Recall, the slope-intercept equation for a line is expressed in these terms: y = mx + b Where: m is the slope of the line b is the y-intercept. If we have determined there is a linear relationship between two variables with covariance and the coefficient of correlation, can we determine a linear function of the relationship?
5 Least Squares Method Just to make things more difficult for students, we typically rewrite this line as: ˆ y b b x 0 1 Read as y-hat! --- Fitted regression line! s b xy where the slope, 1 2 s x b y b x and the intercept, 0 1 Read as ”b naught”
6 Interpretation of the b 0 , b 1
7 Some of the errors will be positive and some will be negative! The problem is that when we add positive and negative values, they tend to cancel each other out. “Best” line: least -squares, or regression line We can then define the error to be the difference between the coordinates and the prediction line. The coordinate of one point: (x i , y i ) ˆ y b b x Predicted value for given x i : i 0 1 i ˆ i 2 “Best” line minimizes y y , the sum of the squared errors. i Error = distance from one point to the line = Coordinate – Prediction
8 Some of the errors will be positive and some will be negative! The problem is that when we add positive and negative values, they tend to cancel each other out. “Best” line: least -squares, or regression line When we square those error lines, we are literally making squares from those lines. We can visualize this as... So we want to find the regression line that minimizes the sum of the areas of these error squares. For this regression line, the sum of the areas of the squares would look like this...
9 Let`s determine the best-fitted line for following data: s b xy b y b x Least Squares Method 1 0 1 2 s x
10 s b xy b y b x Least Squares Method 1 0 1 2 s x
11 s b xy b y b x Least Squares Method 1 0 1 2 s x
12 s b xy b y b x Least Squares Method 1 0 1 2 s x
13 s b xy b y b x Least Squares Method 1 0 1 2 s x Lines of best fit will pivot around the point which represents the mean of X and the mean of the Y variables!
14 s b xy b y b x Least Squares Method 1 0 1 2 s x 2 x x i 2 s n 1
15 s b xy b y b x Least Squares Method 1 0 1 2 s x
16 s b xy b y b x Least Squares Method 1 0 1 2 s x
17 s b xy b y b x Least Squares Method 1 0 1 2 s x
18 s b xy b y b x Least Squares Method 1 0 1 2 s x
19 s b xy b y b x Least Squares Method 1 0 1 2 s x
20 s b xy b y b x Least Squares Method 1 0 1 2 s x
21 s b xy b y b x Least Squares Method 1 0 1 2 s x 2 x x i 2 s n 1
22 s b xy b y b x Least Squares Method 1 0 1 2 s x 2 x x i 2 s n 1
23 s b xy b y b x Least Squares Method 1 0 1 2 s x 2 x x i 2 s n 1
24 s b xy b y b x Least Squares Method 1 0 1 2 s x 2 x x i 2 s n 1
25 s b xy b y b x Least Squares Method 1 0 1 2 s x 2 x x i 2 s n 1
26 s b xy b y b x Least Squares Method 1 0 1 2 s x
27 Line of Best Fit Only for medium to strong correlations...
28 Line of Best Fit
29 Line of Best Fit
30 What line? r measures “closeness” of data to the “best” line. How best? In terms of least squared error:
31 Interpretation of the b 0 , b 1 , ˆ i y x i In a fixed and variable costs model: ˆ y 9.95 2.25 x i i b 0 =9.95? Intercept: predicted value of y when x = 0. b 1 =2.25? Slope: predicted change in y when x increases by 1.
32 Interpretation of the b 0 , b 1 , ˆ i y x i A simple example of a linear equation A company has fixed costs of $7,000 for plant and equipment and variable costs of $600 for each unit of output. What is total cost at varying levels of output? let x = units of output let C = total cost C = fixed cost plus variable cost = 7,000 + 600 x
33 Interpretation of the b 0 , b 1 , ˆ i y x i b 1 , slope, always has the same sign as r, the correlation coefficient — but they measure different things! ˆ y y The sum of the errors (or residuals), , is always 0 i i (zero). x , y The line always passes through the point .
34 Coefficient of Determination When we introduced the coefficient of correlation we pointed out that except for − 1, 0, and +1 we cannot precisely interpret its meaning. We can judge the coefficient of correlation in relation to its proximity to − 1, 0, and +1 only. Fortunately, we have another measure that can be precisely interpreted. It is the coefficient of determination , which is calculated by squaring the coefficient of correlation. For this reason we denote it R 2 .
35 Coefficient of Determination The coefficient of determination measures the amount of variation in the dependent variable that is explained by the variation in the independent variable. The coefficient of determination is R 2 = 0.758 This tells us that 75.8% of the variation in electrical costs is explained by the number of tools. The remaining 24.2% is unexplained.
36 Least Squares Method --- R 2
37 Parameters and Statistics
Recommend
More recommend