( la Shannon) A multi-channel extension A multi-channel extension u - PowerPoint PPT Presentation

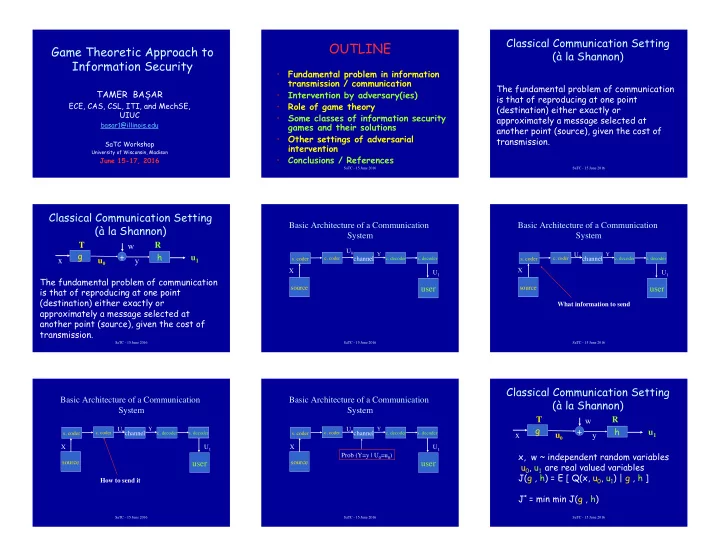
Classical Communication Setting OUTLINE ! Game Theoretic Approach to (à la Shannon) Information Security • Fundamental problem in information transmission / communication The fundamental problem of communication TAMER BA Ș AR • Intervention by adversary(ies) is that of reproducing at one point • Role of game theory ECE, CAS, CSL, ITI, and MechSE, (destination) either exactly or UIUC • Some classes of information security approximately a message selected at basar1@illinois.edu games and their solutions another point (source), given the cost of • Other settings of adversarial transmission. SaTC Workshop intervention University of Wisconsin, Madison • Conclusions / References June 15-17, 2016 SaTC - 15 June 2016 SaTC - 15 June 2016 Classical Communication Setting Basic Architecture of a Communication Basic Architecture of a Communication (à la Shannon) System System T R w U 0 g h Y U 0 Y + u 1 s. coder c. coder channel c. decoder s. decoder s. coder c. coder channel c. decoder s. decoder x u 0 y X X U 1 U 1 The fundamental problem of communication source user source user is that of reproducing at one point (destination) either exactly or What information to send approximately a message selected at another point (source), given the cost of transmission. SaTC - 15 June 2016 SaTC - 15 June 2016 SaTC - 15 June 2016 Classical Communication Setting Basic Architecture of a Communication Basic Architecture of a Communication (à la Shannon) System System T R w g h U 0 Y U 0 Y + u 1 s. coder c. coder channel c. decoder s. decoder s. coder c. coder channel c. decoder s. decoder x u 0 y X U 1 X U 1 x, w ~ independent random variables Prob (Y=y | U 0 =u 0 ) source user source user u 0 , u 1 are real valued variables J(g , h) = E [ Q(x, u 0 , u 1 ) | g , h ] How to send it J * = min min J(g , h) SaTC - 15 June 2016 SaTC - 15 June 2016 SaTC - 15 June 2016

Classical Communication Setting (à la Shannon) A multi-channel extension A multi-channel extension u 1 = h (y 1 ,..,y n ) T R w λ 1 w 1 λ 1 w 1 g h + u 1 × + × + x u 0 y y 1 y 1 v v + + × × h h y 2 y 2 x, w ~ independent random variables g g + + u 1 u 1 x x u 0 w n u 0 w n u 0 , u 1 are real valued actions λ n λ n J(g , h) = E [ Q(x, u 0 , u 1 ) | g , h ] + + × × y n y n u 0 = g (x+v) y i = λ I g (x+v) + w i Standard distortion measure: λ i � s are nonzero constants (gains); J * = min min J(g , γ 1 ) Q(x, u 0 , u 1 ) = k (u 0 ) 2 + (u 1 - x) 2 x, v, w i � s are independent random variables Distortion : Q(x, u 0 , u 1 ) = k (u 0 ) 2 + (u 1 - x) 2 or with k=0 & E[ (u 0 ) 2 ] ≤ α SaTC - 15 June 2016 SaTC - 15 June 2016 SaTC - 15 June 2016 Multi-agent networked systems as graphs Multiple Serial Decision Units A multi-sensor transmission Network is a w 1 w 0 w m-1 connected graph g 1 z …. g …. h 1 h m + + x + v + y m u m Receiver x 1 u 0 Nodes are g 2 + h x 2 agents / dynamic x ~ N(0, σ x 2 ), w i ~ N(0, σ w 2 ), v ~ N(0, σ v 2 ) Source (S) + y systems /mobile w n g n u 1 J(g 0 , h [1,m] ) = E [ Q(x, u 0 , u [1,m] ) | g 0 , h [1,m] ] + x n Links are one of three types of Design {(g 1 , …, g n ), h} to minimize a Q(x, u 0 , u [1,m] ) = (u m – x) 2 + Σ i=1 m (u i-1 ) 2 connections distortion at receiver, with w i, z noises SaTC - 15 June 2016 SaTC - 15 June 2016 SaTC%&%15%June%2016 % Multi-agent networked systems Some nodes could be Intrusion/Intervention by an Adversary adversarial: as graphs • jamming communication Links are one of • interrupting collaboration Passive attack three types of • breaking physical links • Eavesdropping (on transmission—a passive attack) connections: Active attacks • Communication Leads to a game situation • Jamming (communication channels) • Collaboration • Denial of service ! Conflic4ng%interests% • Physical • Message distortion (by flipping bits—active attack) %between%mul4ple%% • Node capture and cloning (physically capturing sensor ! Layered coopera4ve%as%well%as% nodes, replicatings the nodes, and deploying into the graphs non&coopera4ve%agents% network) SaTC - 15 June 2016 SaTC%&%15%June%2016 % SaTC%&%15%June%2016 %

Back to Classical Setting but with Back to Classical Setting but with Aerial Jamming Attack on the Channel Jammed Channel Jammed CommNet of a team of UAVs v v w w g g h h + + u 1 u 1 x u 0 y x u 0 y The jammer wants to maximize the time for which v is the jamming signal generated by Q: What is known about the capabilities, communication can be jammed. information access, and objectives of J? the adversary (J) The two UAVs want to minimize the time for which communication remains jammed. SaTC - 15 June 2016 SaTC - 15 June 2016 SaTC - 15 June 2016 Back to Classical Setting but with Back to Classical Setting but with Back to Classical Setting but with Channel Jammed Channel Jammed Channel Jammed v v v w w w g g g h h h + + + u 1 u 1 u 1 x u 0 y x u 0 y x u 0 y Q: What is known about the capabilities, Q: What is known about the capabilities, Standard distortion measure information access, and objectives of J? information access, and objectives of J? Q IJ (x, u 0 , u 1 , v) = k 0 (u 0 ) 2 + (u 1 - x) 2 with J’s constraint E[v 2 ] ≤ α For example: E[v 2 ] ≤ α J has access to some information, I J , or on x and u 0 ! v = μ ( I J ) Q IJ (x, u 0 , u 1 , v) = k 0 (u 0 ) 2 + (u 1 - x) 2 – k J v 2 Looking for policies ( ( g, h ), μ ) possibly randomized SaTC - 15 June 2016 SaTC - 15 June 2016 SaTC - 15 June 2016 Back to Classical Setting but with Back to Classical Setting but with Upper and lower values, Saddle Channel Jammed Channel Jammed Point, and Nonzero-sum Games v v v inf ( g, h ) sup μ R( g, h , μ ) =: R* (UV of ZSG) w w w g g g h h h + + + u 1 u 1 u 1 x u 0 y x u 0 y x u 0 y Lower value (LV) is: R(g, h, μ ) := E[ Q IJ (x, u 0 , u 1 , v) | ( g, h ),, μ ] sup μ inf ( g, h ) R( g, h , μ ) ≤ R* R(g, h, μ ) := E[ Q IJ (x, u 0 , u 1 , v) | ( g, h ), μ ] R is what the system cares about and hence If equal, then there is “value”, and possibility J has access to some information, I J , a reasonable approach is of SP: A triple ( g*, h* , μ *) such that inf ( g, h ) sup μ R( g, h , μ ) =: R* (UV of ZSG) on x and u 0 ! v = μ ( I J ) R( g*, h* , μ ) ≤ R( g*, h* , μ *) ≤ R( g, h , μ *) Looking for policies ( ( g, h ), μ ) If J behaves differently, then system does for all g, h , μ no worse than R* using the same policy pair. possibly randomized SaTC - 15 June 2016 SaTC - 15 June 2016 SaTC - 15 June 2016