Intuitionistic Fixed Point Logic and Program Extraction (with Prawf) - PowerPoint PPT Presentation

Intuitionistic Fixed Point Logic and Program Extraction (with Prawf) Olga Petrovska (joint work with Ulrich Berger (SU) and Hideki Tsuiki (Kyoto University)) 6-8 April, BCTCS 2020 (Coronavirus Edition ) This work was supported by the Marie Curie International Re- search Stafg Exchange Schemes Computable Analysis (PIRSES-GA- 2011-294962) and Correctness by Construction (FP7-PEOPLE-2013- IRSES-612638) as well as the Marie Curie RISE project Computing with Infinite Data (H2020-MSCA-RISE-2016-731143) and the EPSRC Doctoral Training Grant No. 1818640.

Prawf NEW Motivation Creating a formal system exploiting Curry-Howard isomorphism to extract useful and ‘correct-by-construction’ programs from proofs about abstract mathematics. Existing systems: • Minlog (H. Schwichtenberg): http://www.mathematik. uni-muenchen.de/~logik/minlog/index.php • Nuprl, Isabelle, Coq etc. • 1

Prawf NEW Motivation Creating a formal system exploiting Curry-Howard isomorphism to extract useful and ‘correct-by-construction’ programs from proofs about abstract mathematics. Existing systems: • Minlog (H. Schwichtenberg): http://www.mathematik. uni-muenchen.de/~logik/minlog/index.php • Nuprl, Isabelle, Coq etc. • 1

Prawf NEW Motivation Creating a formal system exploiting Curry-Howard isomorphism to extract useful and ‘correct-by-construction’ programs from proofs about abstract mathematics. Existing systems: • Minlog (H. Schwichtenberg): http://www.mathematik. uni-muenchen.de/~logik/minlog/index.php • Nuprl, Isabelle, Coq etc. • 1

Prawf NEW Motivation Creating a formal system exploiting Curry-Howard isomorphism to extract useful and ‘correct-by-construction’ programs from proofs about abstract mathematics. Existing systems: • Minlog (H. Schwichtenberg): http://www.mathematik. uni-muenchen.de/~logik/minlog/index.php • Nuprl, Isabelle, Coq etc. • 1

Motivation Creating a formal system exploiting Curry-Howard isomorphism to extract useful and ‘correct-by-construction’ programs from proofs about abstract mathematics. Existing systems: • Minlog (H. Schwichtenberg): http://www.mathematik. uni-muenchen.de/~logik/minlog/index.php • Nuprl, Isabelle, Coq etc. • 1 Prawf NEW

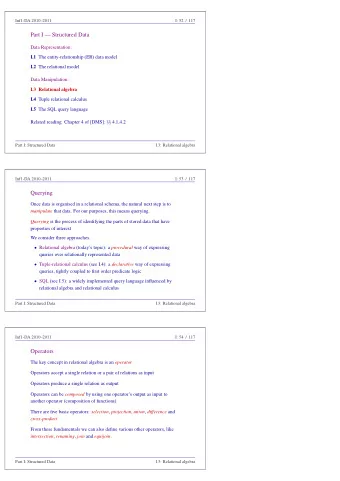
Agenda • Intuitionistic Fixed Point Logic • Realizability • Soundness • Demo 2

Intuitionistic Fixed Point Logic (IFP) as a schema (2) Terms ( First-order logic with lambda abstractions and fixed point operators 3 IFP is a schema (1) Sorts ι, ι 1 , . . . as names for spaces of abstract mathematical objects. ⃗ t ) that include variables , constants of fixed sorts ι and function symbols types ⃗ ι → ι . (3) Predicate constants of fixed arities ( ⃗ ι ) . ⃗ Formulas ∋ A , B ::= P ( t ) | A ∧ B | A ∨ B | A → B | ∀ x A | ∃ x A X | P | λ⃗ Predicates ∋ P , Q ::= x A | µ Φ | ν Φ Operators ∋ Φ , Ψ ::= λ X P ( P is strictly positive in X )

Intuitionistic Fixed Point Logic (IFP) ind • Axioms consisting of closed disjunction-free formulas coind cocl • Intuitionistic Predicate Logic 4 cl • Inductions and Coinduction Natural deduction with equality Φ( P ) ⊆ P Φ( µ Φ) ⊆ µ Φ µ Φ ⊆ P P ⊆ Φ( P ) ν Φ ⊆ Φ( ν Φ) P ⊆ ν Φ e.g., ∀ x , y ( x + y = y + x )

Realizability and RIFP A realizer is an object that “realizes” a formula from a formal theory, i.e. serves as a confirmation of its truth. IFP for Realisers (RIFP) The Scott domain of realizers is defined by the recursive domain equation 5 D = Nil + Lt ( D ) + Rt ( D ) + Pair ( D × D ) + F ( D → D ) where + denotes the separated sum, × the Cartesian product and D → D is the continuous function space.

Non-Computational and Harrop Expressions A Harrop expression contains no disjunction or free predicate A non-computational expression contains neither disjunctions nor free predicate variable. 1 predicate variable is not free in the premise of an implication 6 variable at a strictly positive position 1 .

Realizability and Simplified Realizability We assing to every realizers for realizers for realizers 7 • non-Harrop formula A a predicate R ( A ) with one argument for • non-Harrop predicate P a predicate R ( P ) with an extra argument • non-Harrop operator Φ an operator R (Φ) with an extra argument • Harrop formula A a formula H ( A ) • Harrop predicate P a predicate H ( P ) of the same arity • Harrop operator Φ an operator H (Φ) of the same arity

Realizability interpretation 8

Simple means that no sub-expression (of an expression in question) Soundness 9 Γ , ∆ ⊢ IFP A ∗ ⇒ H (Γ) ,⃗ a r ∆ ⊢ RIFP p r A , where FV ( p ) ⊆ ⃗ a . *The admissibility condition is that either Φ and P are both Harrop or both non-Harrop or Φ is Harrop and simple and P is non-Harrop. of a form µ Φ or ν Φ contains a predicate variable X free.

IFP’ and the Soundness Theorem Def Hideki Tsuiki suggested creating IFP’ to get rid of the admissibility where X and Y are fresh variables. 10 extraction implementation. restriction. This also proved to be useful for simplifying program Monotonicity of the operator Φ : Mon (Φ) = X ⊆ Y → Φ( X ) ⊆ Φ( Y ) Φ( P ) ⊆ P Mon (Φ) IND’ (Φ , P ) ( ∗ ) µ (Φ) ⊆ P P ⊆ Φ( P ) Mon (Φ) COIND’ (Φ , P ) ( ∗ ) P ⊆ ν (Φ) ( ∗ ) free assumptions in the proof of Mon (Φ) must not contain X or Y free.

Soundness proof i Proof by induction on the length of IFP’ derivations. 11 Γ , ∆ ⊢ IFP ′ A ⇒ H (Γ) ,⃗ a r ∆ ⊢ RIFP p r A , where FV ( p ) ⊆ ⃗ a .

Soundness proof ii * Proven by a separate lemma, which includes a number of equivalences like above 12 Ind ′ . Assume ⊢ IFP ′ (Φ( P ) ⊆ P ) , where Φ( P ) = Q [ P / X ] and ⊢ IFP ′ Mon (Φ) , i.e. X ⊆ Y → Q ⊆ Q [ Y / X ] . • I.h. 1 nH ⊢ RIFP s r (Φ( P ) ⊆ P ) ; • I.h. mon nH ⊢ RIFP m r ( Mon (Φ)) ; If Φ and P are non-Harrop show: f r ( µ (Φ) ⊆ P ) R ( µ Φ) ⊆ f − 1 ◦ R ( P ) f r ( Q ⊆ P ) ≡ R ( Q ) ⊆ f − 1 ◦ R ( P ) ∗ ≡ R ( µ ( λ X Q )) ⊆ f − 1 ◦ R ( P ) = since Φ = λ X Q X R ( Q ))) ⊆ f − 1 ◦ R ( P ) ( µ ( λ ˜ = since R ( µ Φ) = µ ( R (Φ)) and R ( λ X Q ) = λ ˜ X ( R ( Q ))

Soundness proof iii (3) assumptions. (a) If RIFP proves a r A from assumptions that do not contain the predicate variable X and if P is a by the equivalences lemma By s.p. induction, it is enough to show 13 (2) (1) R ( Q )[ f − 1 ◦ R ( P ) / ˜ X ] ⊆ f − 1 ◦ R ( P ) By i.h. 1 nH we have: s r (Φ( P ) ⊆ ( P )) , which is equivalent to R ( Q [ P / X ]) ⊆ s − 1 ◦ R ( P ) By i.h. mon nH we have m r Mon (Φ) and by Lemma (a) this implies m r ( Mon (Φ)[ P / Y ]) Writing out Mon (Φ)[ P / Y ] we obtain X ⊆ P → Q ⊆ Q [ P / X ] . Hence, 3 can be rewritten as ∀ g ( g r ( X ⊆ P ) → ( m g ) r ( Q ⊆ Q [ P / X ])) ∀ g ( R ( X ) ⊆ g − 1 ◦ R ( P ) → R ( Q ) ⊆ ( m g ) − 1 ◦ R ( Q [ P / X ])) ≡ X ⊆ g − 1 ◦ R ( P ) → R ( Q ) ⊆ ( m g ) − 1 ◦ R ( Q [ P / X ])) ∀ g (˜ = by def. of R ( X ) non-Harrop predicate of the same arity as X , then RIFP proves a r ( A [ P / X ]) from the same

Soundness proof iv by the equivalences lemma arbitrary predicate constant that does not appear in any axiom. X is an by 2 14 X ⊆ g − 1 ◦ R ( P ) → R ( Q ) ⊆ ( m g ) − 1 ◦ R ( Q [ P / X ])) ∀ g (˜ X = f − 1 ◦ R ( P ) and use Lemma (b), we get If we define g as f and ˜ R ( Q )[ f − 1 ◦ R ( P ) / ˜ X ] ⊆ ( m f ) − 1 ◦ R ( Q [ P / X ])) ⊆ ( m f ) − 1 ◦ ( s − 1 ◦ R ( P )) = ( s ◦ m f ) − 1 ◦ R ( P ) Hence, the realiser is recursively defined as f = s ◦ m f (b) If IFP, IFP’, or RIFP proves Γ ⊢ A , then the same system proves Γ[ P / X ] ⊢ A [ P / X ] , Γ[ P / X ] ⊢ A [ P / X ] , where A , P , X are arbitrary formulas, predicates, predicate variables, respectively, and ˆ

Key points before the demo • IFP is a scheme more flexibility, abstraction (e.g., list reversal, translation between representations) • Use of classical logic as long as it is disjunction-free • Prawf is build specifically for the purpose of program extraction 15

Demo 15

Future work • Extensions for sequent calculus proofs (Yvett Szilagyi) • Extension for CFP (Concurrent Fixed Point Logic) • Developing theorems database in Prawf 16

References U. Berger, P. O., and H. Tsuiki. Prawf: An interactive proof system for program extraction. To be published in proceedings of 16th Conference on Computability in Europe, CiE, 2020. U. Berger and O. Petrovska. Optimised program extraction for induction and coinduction. In Sailing Routes in the World of Computation: 14th Conference on Computability in Europe, CiE 2018, Kiel, Germany, July 30 – August 3 , pages 70–80, 2018. U. Berger and H. Tsuiki. Intuitionistic fixed point logic. Unpublished manuscript available on ArXiv, 2019. Prawf: https://prawftree.wordpress.com/ 17

Thank you 17