Introduction to advanced parameter Gradient descent algorithm - PowerPoint PPT Presentation

Introduction to advanced parameter Gradient descent algorithm optimization w 1 d 1 g 1 1. Choose an initial weight vector and let = – . w j w j η d j 2. Let = + . + 1 So far: g j 3. Evaluate . + 1 • What is a neural network? d j g j 4. Let = – . + 1 + 1 • Basic training algorithm: j j 5. Let = + 1 and go to step 2. • Gradient descent • Backpropagation Next: advanced training algorithms Gradient descent review How to improve over gradient descent? Gradient descent: w t ( ) w t ( ) ∆ w t ( ) + 1 = + where, • Must understand convergence properties w t η E w t ∆ ( ) ∇ [ ( ) ] = – • Use second-order information... Two main problems: • Slow convergence η • Trial-and-error selection of : cut number of epochs (training cycles) by orders of Goal magnitude ... how?

First case study Why quadratic error surface? Disadvantages: E 20 ω 1 ω 2 2 2 = + (same as last time) • Too simple/too few parameters globally • NN error surface not quadratic Advantage: 40 2 E • Easy to visualize 20 1.5 0 1 locally • NN error surfaces will be quadratic near a local - 1.5 1.5 ω 2 - 1 - 1 0.5 minimum. - 0.5 - 0.5 0 ω 1 0 0 0.5 0.5 - 0.5 1 Will also look at simple nonquadratic error surfaces... Taylor series expansion Hessian matrix Definition : The Hessian matrix of a - Single dimension (from calculus): × W W H W dimensional function E w is defined as, ( ) ( ) ≈ ( ) ( ) x ( ) ( ) x ( ) 2 f x f x 0 f ' x 0 x 0 f '' x 0 x 0 + – + – E w H ∇ [ ∇ ( ) ] = where, Multi-dimensional error surface: T w ω 1 ω 2 … ω W = 1 ) T b - w ) T H w E w ( ) ≈ E w 0 ( ) ( w w 0 ( w 0 ( w 0 ) + – + - - – – 2 about some vector w 0 , where, Alternatively: b ∇ E w 0 ( ) = ∂ 2 E H i j = - - - - - - - - - - - - - - - - - - ( , ) ∂ω i ∂ω j ∇ [ ∇ E w 0 ( ) ] ( not just a German mercenary) H Hessian: =

Some linear algebra Gradient descent convergence rate Definition : For a × square matrix , the eigenvalues W W H Near local minimum: λ are the solution of, λ min > 0 (why?) λ I W H – = 0 Definition : A square matrix is positive-definite , if and H Convergence governed by: only if all its eigenvalues are greater than zero. If a λ i matrix is positive-definite, then, λ min   - - - - - - - - - - - - v T H v v   > ∀ ≠ λ max 0 , 0 . Learning rate bound: > H • Quadratic error surface: 0 2 < η < 0 - - - - - - - - - - - - λ max H > • Arbitrary error surface: 0 near local minimum. Simple Hessian example Simple Hessian example (continued) 20 ω 1 ω 2 20 ω 1 ω 2 E E 2 2 2 2 = + = + Second partial derivatives: First partial derivatives: ∂ 2 E ∂ 2 E ∂ 2 E ∂ 2 E ∂ ∂ E E 40 ω 1 2 ω 2 - - - - - - - - - - = 40 - - - - - - - - - - = 2 - - - - - - - - - - - - - - - - - - - - = - - - - - - - - - - - - - - - - - - - - = 0 - - - - - - - - - = - - - - - - - - - = ∂ω 1 ∂ω 2 ∂ω 2 ∂ω 1 ∂ω 1 ∂ω 2 ∂ ω 1 ∂ ω 2 2 2 Hessian: Second partial derivatives: ∂ 2 E ∂ 2 E ∂ 2 E ∂ 2 E 40 0 H - - - - - - - - - - = 40 - - - - - - - - - - = 2 - - - - - - - - - - - - - - - - - - - - = - - - - - - - - - - - - - - - - - - - - = 0 = ∂ω 1 ∂ω 2 ∂ω 2 ∂ω 1 ∂ω 1 ∂ω 2 2 2 0 2

Simple Hessian example (continued) Computation of eigenvalues λ 1 0 40 0 λ I 2 H – = 0 – = 0 0 1 0 2 40 0 H = 0 2 λ – 40 0 = 0 λ 0 – 2 What are the eigenvalues? ( λ ) λ ( ) – 40 – 2 = 0 λ min = 2 λ max = 40 Learning rate bounds Convergence examples η = 0.01 2 λ min = 2 1.5 λ max = 40 1 ω 2 0.5 0 2 < η < 0 - - - - - - - - - - - - λ max - 0.5 - 1.5 - 1 - 0.5 0 0.5 1 ω 1 2 < η < - - - - - - 0 = 0.05 (same as fixed-point derivation) 719 steps 40

Convergence examples Convergence examples η η = 0.04 = 0.05 2 2 1.5 1.5 1 1 ω 2 0.5 0.5 0 0 - 0.5 - 0.5 - 1.5 - 1 - 0.5 - 1.5 - 1 - 0.5 0 0.5 1 0 0.5 1 ω 1 ω 1 175 steps no convergence Basic problem: “long valley with steep Solution sides” What characterizes a “ long valley with steep sides?” • Fixed learning rate is the problem • Answer: different learning rates for each weight. Length of contour lines proportional to: 1 1 - - - - - - - - - - - - - - - - - - - - and λ 1 λ 2 Key question: how to achieve automatically? Small ratios: λ min   - - - - - - - - - - - -   λ max So what can we do about this?

Heuristic extension: momentum Gradient descent algorithm µ w 1 d 1 g 1 Gradient descent with momentum: 1. Choose an initial weight vector and let = – . w j w j η d j w t w t w t ( ) ( ) ∆ ( ) 2. Let = + . + 1 = + + 1 g j w 0 η E w 0 ∆ ( ) ∇ [ ( ) ] 3. Evaluate . = – + 1 ∆ w t ( ) η E w t ∇ [ ( ) ] µ∆ w t ( ) > ≤ µ < t d j g j = – + – 1 , 0 , 0 1 4. Let = – . + 1 + 1 j j 5. Let = + 1 and go to step 2. Notes: w t w t w t ∆ ( ) ( ) ( ) • dependent on and – 1 Ideally, high effective learning rate in shallow dimensions • • Little effect along steep dimensions Analyzing momentum term Analyzing momentum term Assumption (shallow region): Shallow regions: assume, ∇ E w t ( ) ≈ ∇ E w 0 ( ) g ∈ { 1 2 … , , } t ∇ E w t ( ) ≈ ∇ E w 0 ( ) g ∈ { 1 2 … , , } = , t = , In general, Then: t   µ t w 0 η g ∆ ( ) + 1  g  η 1 – ∑ = – µ s ∆ w t ( ) ≈ η g   – = – - - - - - - - - - - - - - - - - - - - - -   µ   1 – s w 1 η g µ w 0 η g 1 = 0 ∆ ( ) ≈ ∆ ( ) ( µ ) – + = – + In the limit: w 2 η g µ w 1 η g η g 1 ∆ ( ) ≈ ∆ ( ) µ [ ( µ ) ] – + = – + – + η – ∆ w t ( ) ≈ - g lim - - - - - - - - - - - - - - - - ( µ ) w 2 η g 1 ∆ ( ) ≈ ( µ µ 2 ) 1 – t → ∞ – + +

Analyzing momentum term Analyzing momentum term Steep regions: oscillations Effective learning rate (shallow regions): η ⁄ ( µ ) 1 – ∇ E w t [ ( ) ] ≈ ∇ E w t [ ( ) ] + 1 – Net effect (ideally): little Momentum Convergence examples η 0.01 µ , = = 0.0 2 Advantage: 1.5 Increase effective learning rate in shallow regions • 1 ω 2 0.5 0 Disadvantages: - 0.5 - 1.5 - 1 - 0.5 0 0.5 1 • Yet another parameter to hand tune ω 1 µ • If not carefully chosen, can do more harm than good 719 steps

Convergence examples Convergence examples η 0.01 µ , η 0.01 µ , = = 0.5 = = 0.9 2 2 1.5 1.5 1 1 ω 2 ω 2 0.5 0.5 0 0 - 0.5 - 0.5 - 1.5 - 1 - 0.5 - 1.5 - 1 - 0.5 0 0.5 1 0 0.5 1 ω 1 ω 1 341 steps 266 steps Convergence examples Convergence examples η 0.04 µ , η 0.04 µ , = = 0.0 = = 0.5 2 2 1.5 1.5 1 1 ω 2 ω 2 0.5 0.5 0 0 - 0.5 - 0.5 - 1.5 - 1 - 0.5 - 1.5 - 1 - 0.5 0 0.5 1 0 0.5 1 ω 1 ω 1 175 steps 60 steps

Convergence examples Convergence examples: summary η 0.04 µ , = = 0.9 2 1.5 µ µ µ 1 = 0.0 = 0.5 = 0.9 0.5 ω 2 719 341 266 η = 0.01 0 175 60 272 η = 0.04 - 0.5 - 1 - 1.5 - 1 - 0.5 0 0.5 1 ω 1 272 steps Heuristic extensions to gradient descent Heuristic extensions to gradient descent Momentum popular in neural network community. • Individual learning rates: ( ) g i t ( t ) ∆ η i γ g i – 1 = (problems?) Many other heuristic attempts (some examples): ρ σ • Adaptive learning rate (what should and be?) ρη old ∆ < E • Quickprop: local independent quadratic assumption:  0 η new  = ση old ∆ E >  0 ( ) t g i ( ) ( ) t - ω i t ∆ ω i ∆ + 1 - - - - - - - - - - - - - - - - - - - - - - - - - - - - - = (problems?) ( ) ( ) t t g i g i – 1 – η max 2 λ max ⁄ • = (what’s the problem here?)

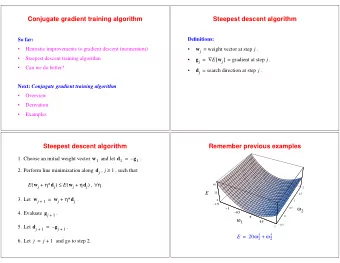
Heuristic extensions to gradient descent Steepest descent Problems: Gradient descent: w t ( ) w t ( ) ∆ w t ( ) • Additional hand-tuned parameters + 1 = + Independence of weight assumptions where, • ∆ w t ( ) η E w t ∇ [ ( ) ] = – More principled approach is desirable. Question: why take all those little tiny steps? Steepest descent: gradient descent with line Steepest descent minimization Question: Do we need to compute ? ∂ E ∂η ⁄ d t ( ) 1. Define search direction : d t E w t ( ) ∇ [ ( ) ] = – Answer: No. Use one-dimensional line search , which requires only evaluation of E η ( ) . 2. Minimize: E η ( ) ≡ E w t [ ( ) η d t ( ) ] + such that: E η∗ ( ) ≤ E η ( ) ∀ η Line search: two steps , 3. New update: 1. Bracket minimum η∗ d t w t w t ( ) ( ) ( ) + 1 = + (problems?) 2. Line minimization