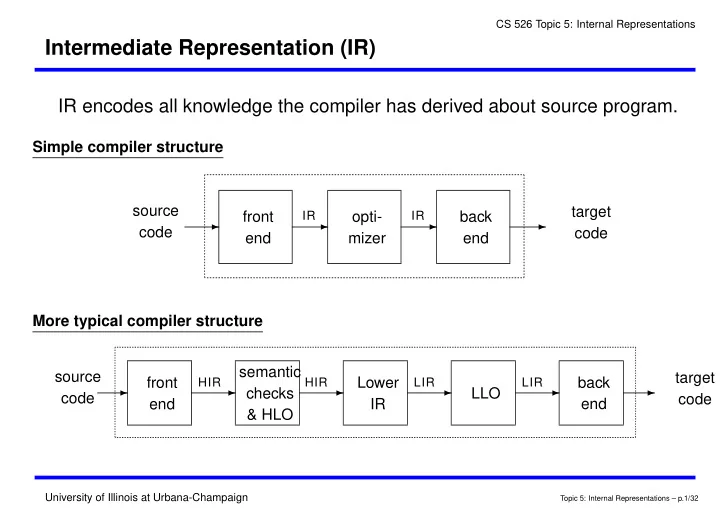

CS 526 Topic 5: Internal Representations Intermediate Representation (IR) IR encodes all knowledge the compiler has derived about source program. Simple compiler structure source target ✲ ✲ ✲ ✲ front IR opti- IR back code code end mizer end More typical compiler structure semantic source target ✲ ✲ ✲ ✲ ✲ ✲ front Lower back HIR HIR LIR LIR checks LLO code code end end IR & HLO University of Illinois at Urbana-Champaign Topic 5: Internal Representations – p.1/32
CS 526 Topic 5: Internal Representations Components and Design Goals for an IR Components of IR Code representation : actual statements or instructions Symbol table with links to/from code Analysis information with mapping to/from code Constants table : strings, initializers, ... Storage map : stack frame layout, register assignments Design Goals for an IR? There is no universally good IR. Many forms of IR have been used. The right choice depends strongly on the goals of the compiler system. University of Illinois at Urbana-Champaign Topic 5: Internal Representations – p.2/32
CS 526 Topic 5: Internal Representations Common Code and Analysis Representations Analysis representations Code representations May have several at a time Usually have only one at a time Common choices : Common alternatives : Control Flow Graph (CFG) Abstract Syntax Tree (AST) Symbolic expression DAGs SSA form + CFG Data dependence graph 3-address code [+ CFG] (DDG) Stack code SSA form Influences : Points-to graph / Alias sets semantic information Call graph types of optimizations Influences : ease of transformations analysis capabilities speed of code generation optimization capabilities size University of Illinois at Urbana-Champaign Topic 5: Internal Representations – p.3/32
CS 526 Topic 5: Internal Representations Categories of IRs By Structure Linear IRs Graphical IRs pseudo-code for abstract machine trees, directed graphs, DAG s many possible semantic levels node / edge data structures tend to be large simple, compact data structures harder to rearrange easier to rearrange Examples : AST, CFG, SSA, DDG, Examples : 3-address, 2-address, Expression DAG, Points-to graph accumulator, or stack code Hybrid IRs as the Code Representation CFG + 3-address code (SSA or non-SSA) CFG + 3-address code + expression DAG AST (for control flow) + 3-address code (for basic blocks) AST (for control flow) + expression DAG (for basic blocks) University of Illinois at Urbana-Champaign Topic 5: Internal Representations – p.4/32
CS 526 Topic 5: Internal Representations Abstract syntax tree An Abstract Syntax Tree ( AST ) is a simplified parse tree. It retains syntactic structure of code. Well-suited for source code Widely used in source-source translators Captures both control flow constructs and straight-line code explicitly Traversal and transformations are both relatively expensive both are pointer-intensive transformations are memory-allocation-intensive University of Illinois at Urbana-Champaign Topic 5: Internal Representations – p.5/32
CS 526 Topic 5: Internal Representations Abstract syntax tree: Examples University of Illinois at Urbana-Champaign Topic 5: Internal Representations – p.6/32
CS 526 Topic 5: Internal Representations Directed acyclic graph Example A Directed Acyclic Graph (DAG) is similar to an x ← 2*y + sin(2*x) AST but with a unique node for each value . z ← x / 2 Advantages ← � ❅ sharing of values is explicit ✠ � ❅ ❘ z 1 / exposes redundancy (value computed ✁ ❈ twice) ✁ ❈ ← ✁ ❈ � ❅ ⇒ powerful representation for symbolic ex- ✁ ☛ ❈ ✠ � ❘ ❅ pressions x 1 + ❈ � ❅ ❈ ✠ � ❘ ❅ ❈ sin Disadvantages * ❈ � ❆ ❈ ✠ � ❄ difficult to transform (e.g., delete a stmt) ❆ y 0 ❈❈ * ❆ ❲ � ❅ not useful for showing control flow structure ❆ ❯ ✠ � ❅ ❘ 2 x 0 ⇒ Better for analysis than transformation University of Illinois at Urbana-Champaign Topic 5: Internal Representations – p.7/32
CS 526 Topic 5: Internal Representations Control Flow Graph: CFG Definitions Basic Block ≡ a consecutive sequence of statements (or instructions) S 1 . . . S n such that (a) the flow of control must enter the block at S 1 , and (b) if S 1 is executed, then S 2 . . . S n are all executed in that order (unless one of the statements causes the program to halt). Leader ≡ the first statement of a basic block Maximal Basic Block ≡ a maximal-length basic block CFG ≡ a directed graph (usually for a single procedure) in which: Each node is a single basic block There is an edge b 1 → b 2 if control may flow from last stmt of b 1 to first stmt of b 2 in some execution NOTE: A CFG is a conservative approximation of the control flow! Why? University of Illinois at Urbana-Champaign Topic 5: Internal Representations – p.8/32
CS 526 Topic 5: Internal Representations Examples 1 - Conditional Control Flow “switch” statement in C : Conditional branch in C : stmtlist 0 stmtlist 0 switch (V) { if (x == y) case 1: stmtlist 1 stmtlist 1 case 2: stmtlist 2 else . . . stmtlist 2 case n: stmtlist n stmtlist 3 default: stmtlist n } stmtlist n +1 University of Illinois at Urbana-Champaign Topic 5: Internal Representations – p.9/32
CS 526 Topic 5: Internal Representations Examples 2 - Loops “do-while” loop in C : stmtlist 0 “while” loop in C : do stmtlist 0 stmtlist 1 while (x < k) while (x < k); stmtlist 1 stmtlist 2 stmtlist 2 University of Illinois at Urbana-Champaign Topic 5: Internal Representations – p.10/32
CS 526 Topic 5: Internal Representations Examples 3 - Exceptions “try-catch-finally” in Java : stmtlist 0 try { S 0 ; // may throw S 1 ; // may throw } catch (etype 1 e1) { S 2 ; // simple statement } catch (etype 2 e2) { S 3 ; // simple statement } finally { S 4 ; // simple statement } stmtlist 1 University of Illinois at Urbana-Champaign Topic 5: Internal Representations – p.11/32
CS 526 Topic 5: Internal Representations Dominance in Control Flow Graphs Dominates ≡ B 1 dominates B 2 iff all paths from entry node to B 2 include B 1 . Intuitively, B 1 is always executed before executing B 2 (or B 1 = B 2 ). Which assignments dominate (X+Y)? : Which assignments dominate (X+Y)? : X = 1; X = 1; if (...) if (...) { { Y = 4; Y = 4; ... = X + Y; } ... = X + Y; } University of Illinois at Urbana-Champaign Topic 5: Internal Representations – p.12/32
CS 526 Topic 5: Internal Representations Static Single Assignment (SSA) Form Informally, a program can be converted into SSA form as follows: Each assignment to a variable is given a unique name All of the uses reached by that assignment are renamed. Easy for straight-line code: V ← 4 2V 0 ← 4 ← V + 5 2 ← V 0 + 5 V ← 6 2V 1 ← 6 ← V + 7 2 ← V 1 + 7 What about flow of control? Introduce φ -functions! University of Illinois at Urbana-Champaign Topic 5: Internal Representations – p.13/32
CS 526 Topic 5: Internal Representations Static Single Assignment with Control Flow if (...) if (...) 2-way branch : X = 5; X 0 = 5; else else X = 3; X 1 = 3; X 2 = φ (X 0 , X 1 ); Y = X; Y 0 = X 2 ; While loop : j = 1; j 5 = 1; S : // while (j < x) S : j 2 = φ (j 5 , j 4 ); if (j > = X) if (j 2 > = X) goto E ; goto E ; j = j+1; j 4 = j 2 +1; goto S goto S E : E : N = j; N = j 2 ; University of Illinois at Urbana-Champaign Topic 5: Internal Representations – p.14/32
CS 526 Topic 5: Internal Representations Definition of SSA Form Definition ( φ Functions) : In a basic block B with N predecessors, P 1 , P 2 , . . . , P N , X = φ ( V 1 , V 2 , . . . , V N ) assigns X = V j if control enters block B from P j , 1 ≤ j ≤ N . Properties of φ -functions : φ is not an executable operation. φ has exactly as many arguments as the number of incoming BB edges Think about φ argument V i as being evaluated on CFG edge from predecessor P i to B Definition (SSA form) : A program is in SSA form if: 1. each variable is assigned a value in exactly one statement 2. each use of a variable is dominated by the definition University of Illinois at Urbana-Champaign Topic 5: Internal Representations – p.15/32
CS 526 Topic 5: Internal Representations The SSA Graph Definition (SSA Graph): The SSA Graph is a directed graph in which: Nodes = All definitions and uses of SSA variables Edges = { ( d, u ) : u uses the SSA variable defined in d } Examples Draw the SSA graphs for the examples with control flow University of Illinois at Urbana-Champaign Topic 5: Internal Representations – p.16/32
CS 526 Topic 5: Internal Representations So Where Do We Need Phi Functions? Choices (for each variable X): At every merge point in the CFG? At every merge point after a write to X? At every merge point (after a write to X) that reaches a read of X? At some proper subset of the above merge points? University of Illinois at Urbana-Champaign Topic 5: Internal Representations – p.17/32
Recommend
More recommend