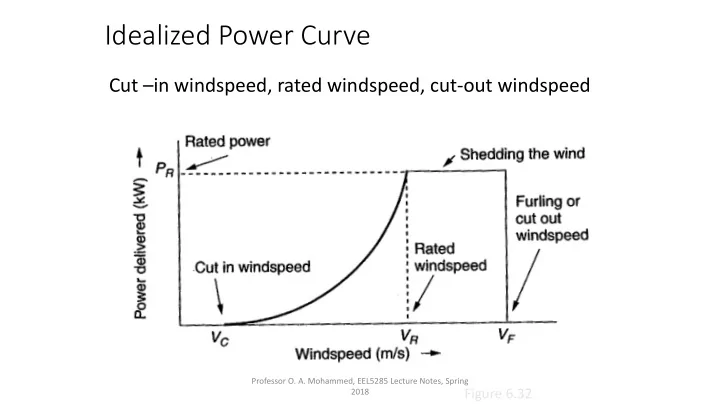
Idealized Power Curve Cut in windspeed, rated windspeed, cut-out - PowerPoint PPT Presentation

Idealized Power Curve Cut – in windspeed, rated windspeed, cut-out windspeed Professor O. A. Mohammed, EEL5285 Lecture Notes, Spring Figure 6.32 2018

Idealized Power Curve • Before the cut-in windspeed , no net power is generated • Then, power rises like the cube of windspeed • After the rated windspeed is reached, the wind turbine operates at rated power (sheds excess wind) • Three common approaches to shed excess wind • Pitch control – physically adjust blade pitch to reduce angle of attack • Stall control (passive) – blades are designed to automatically reduce efficiency in high winds • Active stall control – physically adjust blade pitch to create stall Professor O. A. Mohammed, EEL5285 Lecture Notes, Spring 2018

Idealized Power Curve • Above cut-out or furling windspeed , the wind is too strong to operate the turbine safely, machine is shut down, output power is zero • “Furling” – refers to folding up the sails when winds are too strong in sailing • Rotor can be stopped by rotating the blades to purposely create a stall • Once the rotor is stopped, a mechanical brake locks the rotor shaft in place Professor O. A. Mohammed, EEL5285 Lecture Notes, Spring 2018

Average Power in the Wind • How much energy can we expect from a wind turbine? • To figure out average power in the wind, we need to know the average value of the cube of velocity:     1 1     3 3   P Av A v (6.29) avg   2 2 avg avg • This is why we can’t use average windspeed v avg to find the average power in the wind Professor O. A. Mohammed, EEL5285 Lecture Notes, Spring 2018

Example Windspeed Site Data Figure 6.22 Professor O. A. Mohammed, EEL5285 Lecture Notes, Spring 2018

Wind Probability Density Functions Windspeed probability density function (p.d.f) – between 0 and 1, area under the curve is equal to 1 Professor O. A. Mohammed, EEL5285 Lecture Notes, Spring Figure 6.23 2018

Temperature Correction for Air Density When wind power data are presented, it is often assumed that the air density is 1.225 kg/m 3 ; that is, it is assumed that air temperature is 15 ◦ C (59 ◦ F) and pressure is 1 atmosphere

Altitude Correction for Air Density

IMPACT OF TOWER HEIGHT

An anemometer mounted at a height of 10 m above a surface with crops, hedges, and shrubs shows a windspeed of 5 m/s. Estimate the windspeed and the specific power in the wind at a height of 50 m. Assume 15 ◦ C and 1 atm of pressure.

Estimates of Wind Turbine Energy • Not all of the power in the wind is retained - the rotor spills high-speed winds and low-speed winds are too slow to overcome losses • Depends on rotor, gearbox, generator, tower, controls, terrain, and the wind • Overall conversion efficiency ( C p · η g ) is around 30% P P P  W E B Power to C Power in g Power P Electricity the Wind Gearbox & Rotor Extracted Generator by Blades Professor O. A. Mohammed, EEL5285 Lecture Notes, Spring 2018

Power Mass flow rate

Maximum Rotor Efficiency

Rotor Tip=Speed Ratio

A 40-m, three bladed wind turbine produces 600 kW at a wind speed of 14 m/s. Air density is the standard 1.225 kg/m 3 . Under these conditions, a. At what rpm does the rotor turn when it operates with a TSR of 4.0? b. What is the tip speed of the rotor? c. If the generator needs to turn at 1800 rpm, what gear ratio is needed to match the rotor speed to the generator speed? d. What is the efficiency of the complete wind turbine (blades, gear box,generator) under these conditions?

Economies of Scale • Presently large wind farms produce electricity more economically than small operations • Factors that contribute to lower costs are • Wind power is proportional to the area covered by the blade (square of diameter) while tower costs vary with a value less than the square of the diameter • Larger blades are higher, permitting access to faster winds • Fixed costs associated with construction (permitting, management) are spread over more MWs of capacity • Efficiencies in managing larger wind farms typically result in lower O&M costs (on-site staff reduces travel costs) Professor O. A. Mohammed, EEL5285 Lecture Notes, Spring 2018

Energy Economic Concepts • The economic evaluation of a renewable energy resource requires a meaningful quantification of cost elements • fixed costs • variable costs • We use engineering economics notions for this purpose since they provide the means to compare on a consistent basis • two different projects; or, • the costs with and without a given project Professor O. A. Mohammed, EEL5285 Lecture Notes, Spring 2018

Time Value of Money • Basic notion: a dollar today is not the same as a dollar in a year • Would you rather have $10 now or $50 in five years? • What would a $50,000 purchase you’ll make in 10 years be worth today? • The convention we use is that payments occur at the end of each period Professor O. A. Mohammed, EEL5285 Lecture Notes, Spring 2018

Time Value of Money – Principle and Interest • Principle – the initial sum • Interest – productivity of money over time, money today vs. money tomorrow • Simple interest – not compounded, interest is only paid on the principle amount • Compound interest - when interest is also paid on the interest (what we consider) • Difference between the two is greater when: the interest rate is higher, compounding is more frequent, duration of payments is longer P = principal i = interest value Professor O. A. Mohammed, EEL5285 Lecture Notes, Spring 2018

Compound Interest interest for e.o.p. amount owed amount owed for next period next period 0 P Pi P + Pi = P ( 1 +i ) P ( 1 +i ) + P ( 1 +i ) i = P ( 1 +i ) 2 1 P ( 1 +i ) P ( 1 +i ) i 2 P ( 1 +i ) 2 P ( 1 +i ) 2 i P ( 1 +i ) 2 + P ( 1 +i ) 2 i = P ( 1 +i ) 3 P ( 1 +i ) 3 P ( 1 +i ) 3 i P ( 1 +i ) 3 + P ( 1 +i ) 3 i = P ( 1 +i ) 4 3 P ( 1 +i ) n -1 P ( 1 +i ) n -1 i P ( 1 +i ) n -1 + P ( 1 +i ) n -1 i = P ( 1 +i ) n n -1 P ( 1 +i ) n n The value in the last column for the e.o.p. ( k -1) provides the value in the first column for the e.o.p. k (e.o.p. is end of period) Professor O. A. Mohammed, EEL5285 Lecture Notes, Spring 2018

Terminology • We call (1 + i ) n the single payment compound amount factor   •  We define 1   1 i   and  n    n 1 i is the single payment present worth factor • F is called the future worth; P is called the present worth or present value at interest i of a future sum F Professor O. A. Mohammed, EEL5285 Lecture Notes, Spring 2018

Example: Loan amount P , interest i Loan P for 1 year year 0 P repay P + iP = P ( 1 + i ) at the end of 1 year Loan P for n years year 0 P year 1 ( 1 + i ) P repay/reborrow ( 1 + i ) 2 P year 2 repay/reborrow ( 1 + i ) 3 P year 3 repay/reborrow . ( 1 + i ) n P year n repay Professor O. A. Mohammed, EEL5285 Lecture Notes, Spring 2018

Cash Flows • A cash flow is a transfer of an amount A t from one entity to another at e.o.p. time t • Each cash flow has (1) amount , (2) time , and (3) sign Ex. I take out a loan 0 1 2 3 4 I make equal repayments for 4 years Professor O. A. Mohammed, EEL5285 Lecture Notes, Spring 2018

Cash Flows Diagrams - Overview Convention for cash flows  inflow End of year 1  outflow 0 1 2 3 4 Present Ex. Ex. Take out a loan Revenue collected Initial purchase Payments made Incoming cash flows Outgoing cash flows Professor O. A. Mohammed, EEL5285 Lecture Notes, Spring 2018

Discount Rate • The interest rate i is typically referred to as the discount rate and is denoted by d • In converting a future amount F to a present worth P we can view the discount rate as the interest rate that can be earned from the best investment alternative • A postulated savings of $ 10,000 in a project in 5 years is worth at present    5     5 P F 10,000 1 d 5 Professor O. A. Mohammed, EEL5285 Lecture Notes, Spring 2018

Discount Rate • For d = 0.1, P = $ 6,201, while for d = 0.2, P = $ 4,019 • In general, the lower the discount factor, the higher the present worth • The present worth of a set of costs under a given discount rate is called the life-cycle costs Professor O. A. Mohammed, EEL5285 Lecture Notes, Spring 2018

Equivalence • We represent the time value of money by the standard approach of discounted cash flows • “Discounting” refers to moving cash flows to obtain an equivalent amount in another year • Two cash-flow sets       a b A : t 0,1,2,..., n and A : t 0,1,2,..., n t t under a given discount rate d are said to be equivalent cash-flow sets if their worths, discounted to any point in time, are identical. Professor O. A. Mohammed, EEL5285 Lecture Notes, Spring 2018

Equivalence, Example • Are these cash-flow sets are equivalent with d = 7%? 8,200.40     a b A A t t 2000 2000 2000 2000 2000 0 1 2 4 5 6 7 0 1 2 3 b a Professor O. A. Mohammed, EEL5285 Lecture Notes, Spring 2018