How efficient are binary search trees? Balanced search trees - PowerPoint PPT Presentation

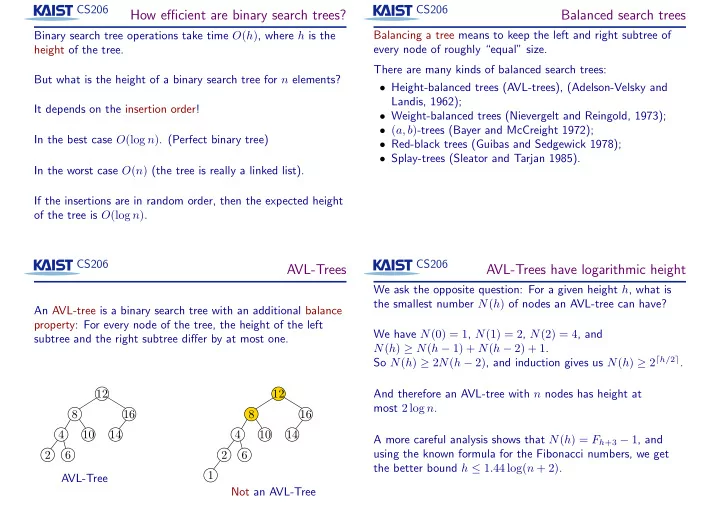
CS206 CS206 How efficient are binary search trees? Balanced search trees Balancing a tree means to keep the left and right subtree of Binary search tree operations take time O ( h ) , where h is the every node of roughly “equal” size. height of the tree. There are many kinds of balanced search trees: But what is the height of a binary search tree for n elements? • Height-balanced trees (AVL-trees), (Adelson-Velsky and Landis, 1962); It depends on the insertion order! • Weight-balanced trees (Nievergelt and Reingold, 1973); • ( a, b ) -trees (Bayer and McCreight 1972); In the best case O (log n ) . (Perfect binary tree) • Red-black trees (Guibas and Sedgewick 1978); • Splay-trees (Sleator and Tarjan 1985). In the worst case O ( n ) (the tree is really a linked list). If the insertions are in random order, then the expected height of the tree is O (log n ) . CS206 CS206 AVL-Trees AVL-Trees have logarithmic height We ask the opposite question: For a given height h , what is the smallest number N ( h ) of nodes an AVL-tree can have? An AVL-tree is a binary search tree with an additional balance property: For every node of the tree, the height of the left We have N (0) = 1 , N (1) = 2 , N (2) = 4 , and subtree and the right subtree differ by at most one. N ( h ) ≥ N ( h − 1) + N ( h − 2) + 1 . So N ( h ) ≥ 2 N ( h − 2) , and induction gives us N ( h ) ≥ 2 ⌈ h/ 2 ⌉ . 12 12 And therefore an AVL-tree with n nodes has height at most 2 log n . 8 16 8 16 4 10 14 4 10 14 A more careful analysis shows that N ( h ) = F h +3 − 1 , and using the known formula for the Fibonacci numbers, we get 2 6 2 6 the better bound h ≤ 1 . 44 log( n + 2) . 1 AVL-Tree Not an AVL-Tree

CS206 CS206 Maintaining balance The four cases of restructuring We have to maintain the balancing condition when we insert or remove nodes in the tree. z z y y Consider the insertion/deletion of a node w . x x Heights change only on the path from the root to w . T 0 T 3 T 1 T 3 T 0 T 2 Let z be the lowest ancestor of w that is now unbalanced. Let T 2 T 1 y be its child of larger height, and x the child of y of larger z z height (outer child in case of equal height). y y We restructure the subtree rooted at z , by moving x , y , and z x x and their subtrees. T 0 T 3 There are four cases. T 2 T 3 T 0 T 1 T 1 T 2 CS206 CS206 Single Rotation Single Rotation z 12 12 y y z 8 16 4 16 x z x y 4 10 14 2 8 14 T 0 x T 1 T 3 2 6 1 6 10 T 3 T 2 T 0 T 1 T 2 1 Left rotation The new subtree at y is balanced since h ( T 0 ) − 1 ≤ h ( T 3 ) ≤ h ( T 0 ) = h ( T 2 ) ≤ h ( T 1 ) ≤ h ( T 0 ) + 1

CS206 CS206 Double rotation Double rotation z z 12 12 y x z x 8 16 6 16 y T 0 y T 0 4 10 14 4 8 14 T 2 T 3 2 6 x 2 5 10 T 1 T 2 T 1 T 3 5 Right rotation around y x Left rotation around z z y h ( T 0 ) = h ( T 1 ) = h ( T 3 ) T 2 h ( T 1 ) − 1 ≤ h ( T 2 ) ≤ h ( T 1 ) T 0 T 1 T 3