Hi The simplest mo del that P(x) ts the data is also - PowerPoint PPT Presentation

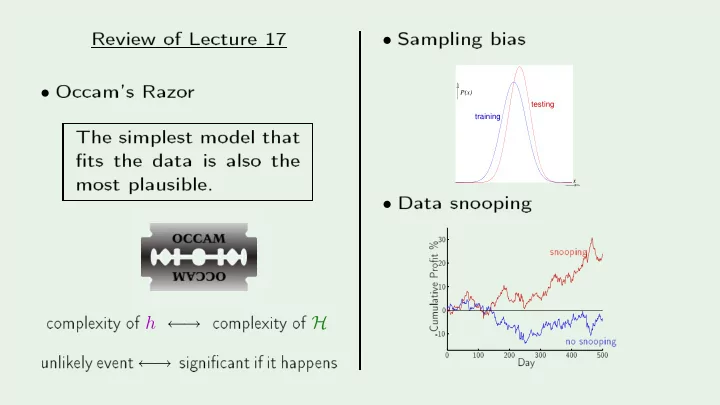
PSfrag repla ements Review of Le ture 17 Sampling bias O am's Razo r • Hi The simplest mo del that • P(x) �ts the data is also the testing training most plausible. Data sno oping x Hi 30 • 20 sno oping 10 % omplexit y of h ← omplexit y of H Pro�t 0 -10 Cumulative unlik ely event ← signi� ant if it happ ens no sno oping 0 100 200 300 400 500 Da y → →

Lea rning F rom Data Y aser S. Abu-Mostafa Califo rnia Institute of T e hnology Le ture 18 : Epilogue Sp onso red b y Calte h's Provost O� e, E&AS Division, and IST Thursda y , Ma y 31, 2012 •

Outline The map of ma hine lea rning Ba y esian lea rning • Aggregation metho ds • A kno wledgments • • Creato r: Y aser Abu-Mostafa - LFD Le ture 18 2/23 M � A L

It's a jungle out there stochastic gradient descent semi−supervised learning overfitting Q learning SVM deterministic noise Gaussian processes data snooping distribution−free learning curves linear regression VC dimension mixture of experts collaborative filtering sampling bias nonlinear transformation neural networks decision trees no free lunch training versus testing RBF noisy targets active learning Bayesian prior linear models weak learners bias−variance tradeoff ordinal regression logistic regression data contamination cross validation ensemble learning hidden Markov models types of learning perceptrons error measures kernel methods graphical models exploration versus exploitation soft−order constraint is learning feasible? Creato r: Y aser Abu-Mostafa - LFD Le ture 18 3/23 Boltzmann machines weight decay clustering regularization Occam’s razor M � A L

The map THEORY TECHNIQUES PARADIGMS models methods VC supervised linear regularization bias−variance neural networks unsupervised validation SVM complexity reinforcement nearest neighbors aggregation bayesian active RBF input processing gaussian processes online SVD Creato r: Y aser Abu-Mostafa - LFD Le ture 18 4/23 graphical models M � A L

Outline The map of ma hine lea rning Ba y esian lea rning • Aggregation metho ds • A kno wledgments • • Creato r: Y aser Abu-Mostafa - LFD Le ture 18 5/23 M � A L

Probabilisti app roa h Extend p robabilisti role to all omp onents de ides whi h h (lik eliho o d) Hi UNKNOWN TARGET DISTRIBUTION UNKNOWN P y P y P y P y ( | ) x INPUT target function f: X Y plus noise DISTRIBUTION Ho w ab out P ( h = f | D ) ? P ( ) x P ( D | h = f ) x , ... , x N 1 DATA SET x ( , ), ... , ( , ) y y D = x x 1 1 N N g ~ f ( ) ( ) x ~ x FINAL LEARNING HYPOTHESIS ALGORITHM g: X Y A HYPOTHESIS SET Creato r: Y aser Abu-Mostafa - LFD Le ture 18 6/23 H Hi M � A L

The p rio r requires an additional p robabilit y distribution: P ( h = f | D ) = P ( D | h = f ) P ( h = f ) is the p rio r P ( h = f | D ) ∝ P ( D | h = f ) P ( h = f ) P ( D ) is the p osterio r P ( h = f ) Given the p rio r, w e have the full distribution P ( h = f | D ) Creato r: Y aser Abu-Mostafa - LFD Le ture 18 7/23 M � A L

Example of a p rio r Consider a p er eptron: h is determined b y w = w 0 , w 1 , · · · , w d A p ossible p rio r on w : Ea h w i is indep endent, unifo rm over [ − 1 , 1] This determines the p rio r over h - Given D , w e an ompute P ( D | h = f ) P ( h = f ) Putting them together, w e get P ( h = f | D ) Creato r: Y aser Abu-Mostafa - LFD Le ture 18 8/23 ∝ P ( h = f ) P ( D | h = f ) M � A L

A p rio r is an assumption Even the most �neutral� p rio r: Hi x is unknown x is random P(x) The true equivalent w ould b e: x −1 1 −1 1 Hi Hi x is unknown x is random δ −a (x ) Creato r: Y aser Abu-Mostafa - LFD Le ture 18 9/23 a x −1 1 −1 1 Hi M � A L

If w e knew the p rio r w e ould ompute P ( h = f | D ) fo r every h ∈ H w e an �nd the most p robable h given the data . . . w e an derive E ( h ( x )) fo r every x = ⇒ w e an derive the erro r ba r fo r every x w e an derive everything in a p rin ipled w a y Creato r: Y aser Abu-Mostafa - LFD Le ture 18 10/23 M � A L

When is Ba y esian lea rning justi�ed? 1. The p rio r is valid trumps all other metho ds 2. The p rio r is irrelevant just a omputational atalyst Creato r: Y aser Abu-Mostafa - LFD Le ture 18 11/23 M � A L

Outline The map of ma hine lea rning Ba y esian lea rning • Aggregation metho ds • A kno wledgments • • Creato r: Y aser Abu-Mostafa - LFD Le ture 18 12/23 M � A L

What is aggregation? Combining di�erent solutions h 1 , h 2 , · · · , h T that w ere trained on D : Hi Regression: tak e an average Hi Classi� ation: tak e a vote a.k.a. ensemble lea rning and b o osting Creato r: Y aser Abu-Mostafa - LFD Le ture 18 13/23 M � A L

Di�erent from 2-la y er lea rning In a 2-la y er mo del, all units lea rn jointly : Hi training data Learning Algorithm In aggregation, they lea rn indep endently then get ombined: Hi Hi training data Learning Algorithm Creato r: Y aser Abu-Mostafa - LFD Le ture 18 14/23 Hi M � A L

T w o t yp es of aggregation 1. After the fa t: ombines existing solutions Example. Net�ix teams merging �blending� 2. Befo re the fa t: reates solutions to b e ombined Example. Bagging - resampling D Hi training data Learning Algorithm Creato r: Y aser Abu-Mostafa - LFD Le ture 18 15/23 Hi M � A L

De o rrelation - b o osting Create h 1 , · · · , h t , · · · sequentially: Mak e h t de o rrelated with p revious h 's: Hi training data Learning Algorithm Emphasize p oints in D that w ere mis lassi�ed Hi Cho ose w eight of h t based on E in ( h t ) Creato r: Y aser Abu-Mostafa - LFD Le ture 18 16/23 M � A L

Blending - after the fa t F o r regression, T Prin ipled hoi e of α t 's: minimize the erro r on an �aggregation data set� pseudo-inverse � g ( x ) = α t h t ( x ) h 1 , h 2 , · · · , h T − → t =1 Some α t 's an ome out negative Most valuable h t in the blend? Un o rrelated h t 's help the blend Creato r: Y aser Abu-Mostafa - LFD Le ture 18 17/23 M � A L

Outline The map of ma hine lea rning Ba y esian lea rning • Aggregation metho ds • A kno wledgments • • Creato r: Y aser Abu-Mostafa - LFD Le ture 18 18/23 M � A L

Course ontent Professo r Malik Magdon-Ismail , RPI Professo r Hsuan-Tien Lin , NTU Creato r: Y aser Abu-Mostafa - LFD Le ture 18 19/23 M � A L

Course sta� Ca rlos Gonzalez ( Head T A ) Ron App el Costis Sideris Do ris Xin Creato r: Y aser Abu-Mostafa - LFD Le ture 18 20/23 M � A L

Filming, p ro du tion, and infrastru ture Leslie Max�eld and the AMT sta� Ri h F agen and the IMSS sta� Creato r: Y aser Abu-Mostafa - LFD Le ture 18 21/23 M � A L

Calte h supp o rt IST - Mathieu Desb run E&AS Division - Ares Rosakis and Mani Chandy Provost's O� e - Ed Stolp er and Melany Hunt Creato r: Y aser Abu-Mostafa - LFD Le ture 18 22/23 M � A L

Many others Calte h T A's and sta� memb ers Calte h alumni and Alumni Asso iation Colleagues all over the w o rld Creato r: Y aser Abu-Mostafa - LFD Le ture 18 23/23 M � A L

To the fond memory of Faiza A. Ibrahim