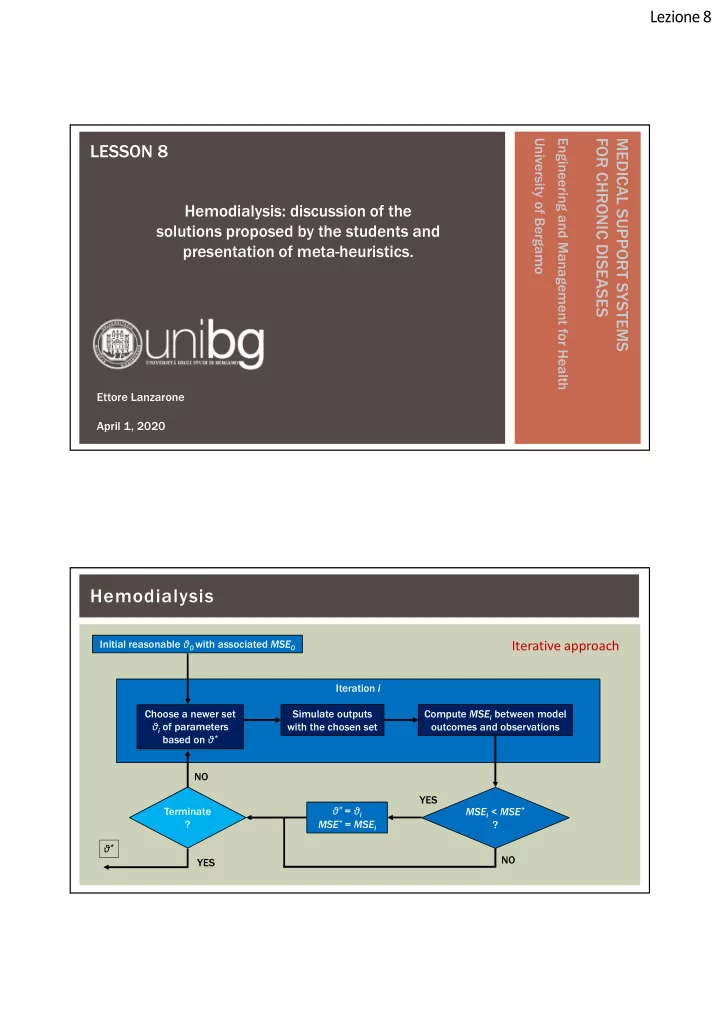

Lezione 8 University of Bergamo Engineering and Management for Health FOR CHRONIC DISEASES MEDICAL SUPPORT SYSTEMS LESSON 8 Hemodialysis: discussion of the solutions proposed by the students and presentation of meta-heuristics. Ettore Lanzarone April 1, 2020 Hemodialysis Initial reasonable θ 0 with associated MSE 0 Iterative approach Iteration i Simulate outputs Compute MSE i between model Choose a newer set θ i of parameters with the chosen set outcomes and observations based on θ * NO YES Terminate θ * = θ i MSE i < MSE * ? MSE * = MSE i ? θ * NO YES
Lezione 8 Hemodialysis This is the general layout. You detailed the blocks according to reasonable choices. More formally, based on the specific blocks, the general iterative approach can be tailored according to one of the literature approaches or a mix of them. For example: • Iterative Local Search • Tabu Search • Gradient method • Simulated annealing Hemodialysis Choose a newer set • Iterative Local Search θ i of parameters based on θ * Randomly choose θ i such that | θ i - θ * | <δ • Tabu Search Randomly choose θ i such that | θ i - θ * | <δ and that θ i was not already tested in any previous iteration • Gradient method If an analytical relationship is available (not our case), choose θ i such that | θ i - θ * | <δ in the direction of maximum decrease of MSE around MSE*
Lezione 8 Hemodialysis • Simulated annealing MSE i < MSE * ? Sometimes accept a worst solution to avoid being trapped in local optimal point. A worst solution is accepted with a probability π i that decreases along with the iterations (π i >π i+1 ) Thus, it is easy to worsen the solution in the first iterations while it becomes less probables after several iterations Hemodialysis Termination Terminate These heuristic approaches converge to the optimal solution ? after an infinite number of iterations. However it is computationally impossible to have infinite iterations. The algorithm has to be stopped at a certain point. Possible criteria are: • After a given number of iterations • When the solution does not improve any more after a certain number of iterations
Lezione 8 Hemodialysis These algorithms are called heuristics of metaheuristics . For a detailed analysis see: Gendrau M. and Potvin J-V (editors) Handbook of Metaheuristics (3rd edition) 2019 Springer, ISBN 978-3-319-91085-7 Available at the Unibg Library LINK Hemodialysis Simulated data vs real observations In both cases you minimize MSE during the iterations (or one of the other validation metrics). What to evaluate? Is the final solution good?
Lezione 8 Hemodialysis SIMULATED DATA In case of simulated data you know the real values of the parameters used to generate the model. You can compute the error between the re-estimated value and the original value. If errors are low, you can trust the model and then apply to real clinical cases. Hemodialysis REAL DATA In case of real data, you do not know the real values of the parameters. You have to assume that a low MSE corresponds to fairly estimated values. Pay attention to non-identifiability issues or equivalent solutions.
Lezione 8 Hemodialysis Refinement of your solutions Hemodialysis Integration of models in the machine
Lezione 8 Hemodialysis Acquire information from the current session Hemodialysis Real time estimation of the patient-specific characteristics Use stored information from the Use previous information of sessions the current session
Lezione 8 Hemodialysis Prediction of the evolution of volumes and solute concentrations Hemodialysis Correction of the machine setting in case of need
Lezione 8 Hemodialysis Approval from the clinician
Recommend
More recommend