Gravitational Potential Energy Lift a book by hand (F ext ) at - PDF document

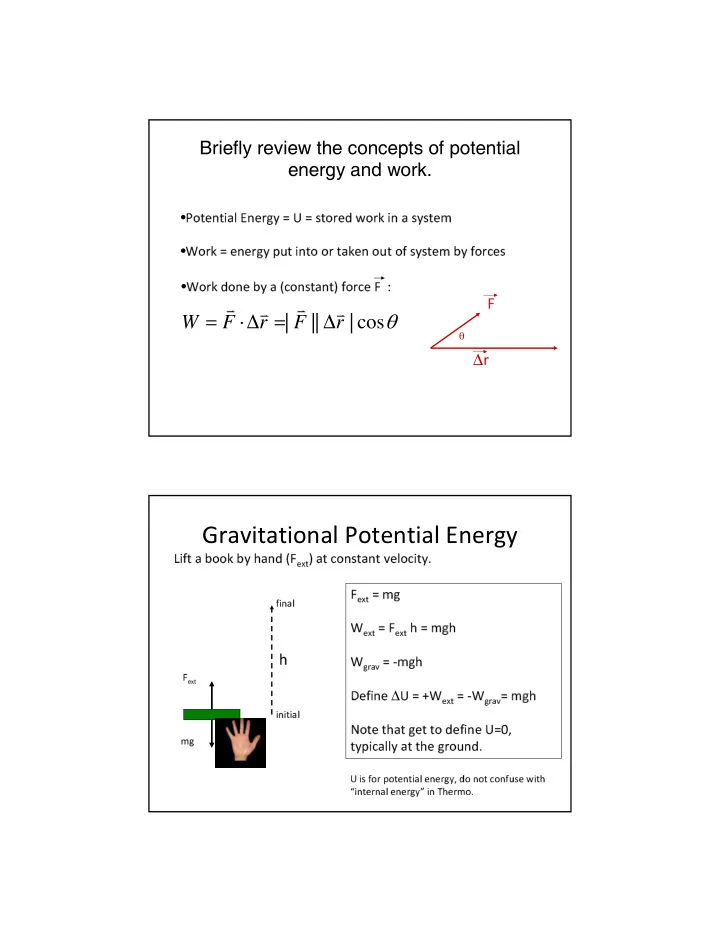
Briefly review the concepts of potential energy and work. • Potential Energy = U = stored work in a system • Work = energy put into or taken out of system by forces • Work done by a (constant) force F : F = ⋅ ∆ = ∆ θ W F v r | F v || r | cos v v θ ∆ r Gravitational Potential Energy Lift a book by hand (F ext ) at constant velocity. F ext = mg final W ext = F ext h = mgh h W grav = -mgh F ext Define ∆ U = +W ext = -W grav = mgh initial Note that get to define U=0, mg typically at the ground. U is for potential energy, do not confuse with “internal energy” in Thermo.

Gravitational Potential Energy (cont) For conservative forces Mechanical Energy is conserved. = + E E U Mech Kin Gravity is a conservative force. Coulomb force is also a conservative force. Friction is not a conservative force. If only conservative forces are acting, then ∆ E Mech =0. ∆ + ∆ = E Kin U 0 Electric Potential Energy Charge in a constant field ∆ U elec = change in U when moving +q from initial to final position. ∆ = − = + = − U U U W W F Ext =-q E f i ext field Final position ∆ = − = − ⋅ ∆ + U W F r v v field field F Field =q E → ∆ = − ⋅ ∆ ∆ r U q E v r v E Initial position + - - - - - - - - - - - - - -

General case What if the E-field is not constant? ∆ = − ⋅ ∆ U q E r v v f Integral over the path ∆ = − ⋅ U q E d r v v from initial (i) position to final (f) ∫ position. i Electric Potential Energy Since Coulomb forces are conservative, it means that the change in potential energy is path independent. f ∆ = − ⋅ U q E d r v v ∫ i

Electric Potential Energy Positive charge in a constant field Electric Potential Energy Negative charge in a constant field

Observations • If we need to exert a force to “push” or “pull” against the field to move the particle to the new position, then U increases. In other words “we want to move the particle to the new position” and “the field resists”. • If we need to exert a force to “hold” the particle so the field will not move the particle to the new position, then U decreases . In other words, “the field wants to move the particle”, and “we resist”. • Both can be summarized in the following statement: “If the force exerted by the field opposes the motion of the particle, the field does negative work and U increases, otherwise, U decreases” Potential Energy between two point charges r +Q 1 +Q 2 Imagine doing work to move the objects from infinitely far apart (initial) to the configuration drawn above (final).

Potential Energy between two point charges ∆ = − = + = − U U U W W f i ext field f ∆ = − = − ⋅ U U U F v d r * Note that force is not v f i ∫ field constant over the path! i f ∆ = − = − ⋅ U U U q E v d r v f i ∫ i Consider Q 1 fixed and move Q 2 from infinity to r. r +Q 1 11 Potential Energy between two point charges r +Q 1 +Q 2 f E-field generated by Q 1 . ∆ = − = − ⋅ U U U q E d r v v ∫ f i Moving Q 2 through the field. i r ⎛ ⎞ 1 Q ∆ = − = − ⎜ ⎟ U U U Q 1 dx 2 4 ⎜ ⎟ ∫ f i πε 2 x ⎝ ⎠ ∞ 0 1 Q Q ∆ = − = U U U 1 2 f i πε 4 r 0

Potential Energy between two point charges We also need to define the zero point for potential energy. This is arbitrary, but the convention is U=0 when all charged objects are infinitely far apart. 1 Q Q ∆ = − = U U U 1 2 U i =U( ∞ )= 0 by our convention. f i πε 4 r 0 1 Q Q = Potential Energy between two U f 1 2 πε 4 r electric charges. 0 E. Potential energy vs. distance

E. Potential Energy of a charge distribution q 1 Potential energy associated to the q 2 field produced by charges q i r 1 r 2 ⎛ ⎞ q q q q q q q 3 = ⎜ + + + ⎟ = U 0 1 2 3 ... 0 i ⎜ ⎟ ∑ πε πε 4 r r r 4 r ⎝ ⎠ i 0 1 2 3 0 i r 3 q 0 For a continuous charge distribution, replace the sum by an integral E. Potential Energy of a charge distribution q 1 To calculate the TOTAL potential q 2 energy we have to consider all the fields produced by all the charges q i r 1 r 2 on the other(n-1) charges q j q 3 q q 1 = i j U ∑ Total πε 4 r r 3 < i j 0 ij q 0 For a continuous charge distribution, replace the sum by an integral

CPS Question Both cases below are for two kQ Q point charges separated by a = U ( r ) 1 2 r distance r. Which graph is correct for two negative charges? A) Left Plot, B) Right Plot U(r) U(r) r r Just like a compressed spring stores potential energy. 17 Electric Field r +Q 1 +Q 2 Earlier we found that not only using forces, but also electric fields was very useful. 1 Q Q 1 Q 1 Q = ˆ = = = F v 1 2 r E 1 r ˆ F q E Q 1 r ˆ v v v 12 πε 1 12 1 2 2 πε 2 πε 2 4 r 4 r 4 r 0 0 0 • Electric Field is the force per unit of charge due to the presence of Q 1 • Electric field from Q 1 is there even if Q 2 is not there. All of the above are vectors!

Electric Potential r +Q 1 +Q 2 We find a similarly useful thing with electric potential energy. 1 Q Q 1 Q 1 Q = = = = U 1 2 V 1 U qV Q 1 12 1 12 1 2 πε πε πε 4 r 4 r 4 r 0 0 0 • Electric potential is the electric potential energy per unit of charge due to the presence of Q 1 • Electric potential from Q 1 is there even if Q 2 is not there. All of the above are scalars! Electric Potential Electric Field is a vector associated with 1 Q = E 1 r ˆ v a source charge Q 1 . 1 πε 2 +Q 1 4 r Units are [Newtons/Coulomb]. 0 Electric potential is a scalar associated with 1 Q = V 1 a source charge Q 1 . 1 πε 4 r Units are [Joules/Coulomb] or [Volts]. 0 V = Voltage = Electric Potential Units are [Volts] = [Joules/Coulomb] U = Electric Potential Energy Units are [Joules] Electric Field Units=[Volts]/[meter]=[Newton]/[Coulomb]

Electric Potential of a point charge 1 q = V πε 4 r 0 Analogy: Electrical pressure or electrical "height" Positive charges want to get away from higher voltage towards lower voltage. Just like a gas wants to move from high to low pressure. Electric Potential of a charge distribution q 1 Potential energy associated to the q 2 field produced by the charges q i r 1 ⎛ ⎞ q q q q q q r 2 = + + + = 0 ⎜ 3 ⎟ 0 i U 1 2 ... ⎜ ⎟ ∑ πε πε 4 r r r 4 r ⎝ ⎠ q 3 i 0 1 2 3 0 i Electric potential due to charges q i r 3 q 0 1 q = V i “test charge” ∑ πε 4 r i 0 i For a continuous charge distribution, replace the sum by an integral

Electric Potential from Electric Field f f ∆ = = − ⋅ = − ⋅ U W F r d r q E v d r v v Ext . ∫ ∫ i i f ∆ U ∆ = = − ⋅ V E v d r v ∫ q i Equipotential surfaces Elevation is a scalar. Contour lines show paths of constant elevation. Gravitational potential V G =gh If I stand at a certain elevation I have a gravitational potential energy [Joules] = mgh=mV G

Equipotential surfaces Electric potential (Voltage) is a scalar. Contour lines show paths of constant Voltage (equipotentials). If a charge q is at a certain Voltage, it has an electrical potential energy [Joules] = qV Equipotential surfaces and field lines • Equi-potential surfaces and field lines are always mutually perpendicular • The Field is not necessarily constant on equipotential surfaces • Larger density of equipotentials means larger variations of V, and larger values of |E|

E. Field and E. potential What is Electric Field? Electric Field is a vector that is analogous to a steepness vector. Steepness cannot have one number at a given position, it depends which direction you look (vector). E. Field and E. potential Given the Electric field vector f ∆ = − = − ⋅ as a function of position, we can V V V E v d r v f i ∫ compute Voltage. i r − ∞ = − ⋅ V ( r ) V ( ) E v d r v V i =V( ∞ )= 0 by our convention. ∫ ∞ r If we integrate the “steepness” over a path, we ∆ = = − ⋅ V V ( r ) E v d r v find the change in elevation. ∫ This does not depend on our path taken. ∞

E. Field and E. potential b b ∆ = − ⋅ = − V E v d r dV v ∫ ∫ a a dV dV dV − = + + = − = − = − dV E dx E dy E dz E ; E ; E ⇒ x y z x y z dx dy dz The Electric field vector is the rate of change ∂ ∂ ∂ V V V = − − − of Voltage in a given direction. ˆ ˆ ˆ E v x y z ∂ ∂ ∂ x y z The Electric field vector “potential gradient” = − ∇ E r V v http://www.falstad.com/vector2de/ CPS question Two identical charge, +Q and +Q, are fixed in space. The electric potential (V) at the point X midway between the charges is: A) Zero V B) Non-Zero ∂ V = − E x ˆ v ∂ x E=0 V=? +Q +Q Point X x +Q +Q 30