graph weight win Rt function its w edges : E on . L Eva - PowerPoint PPT Presentation

t Minimum Cut - ' a ( v. E ) graph weight win Rt function its w edges : E on → .

L Eva , Vs } S = Minimums Cut - S T V - = . w CST ) q :* :* . ' i i EV ' ( SF ) bi partition A cut is Cr of of the any empty ) ( vertices both s , T non are . . set of this E ( crossing cut s , T ) edges =

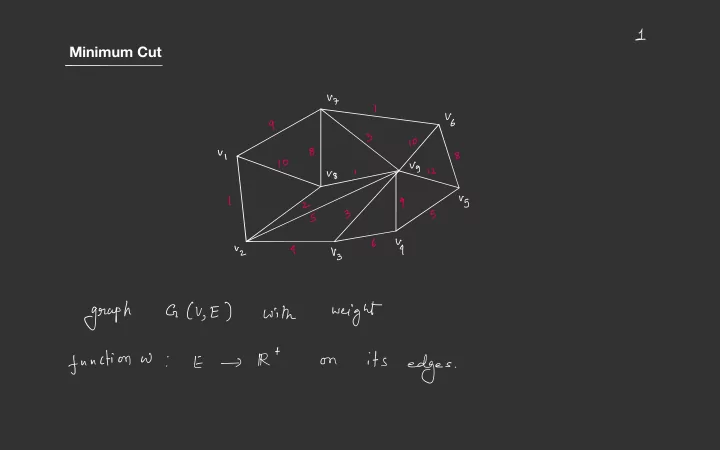
3 Minimum Cut - ✓ 7 I ✓ 6 8 ✓ I 8 go biz b 4 " 2 9 vz weight A is called cat minimum of with the Cr a cut minimum . Problem : G GCV , E. w ) find min cut of Given a . Applications ?

c- V 9 weight minimum of cat A - cut Cst ) is min a parts different Where sand in partition of the me t are . ✓ 7 suppose s =L I 13¥ and 8 ✓ I 8 t= t Vg = go ✓ 9 . OG 12 l Vg wcs.TK#gtsS--Es--Vz3S-- r , vz• b Y 9£ vz T { vi. vz Va 3 = - . , . . by finding find such cat We the maximum can a week ) ( more next flow b/w t this and S on .

g Minot of minced ) the global ( also as G known Cst ) is all cats the minimum over . subroutine If flow maximum we use a OCNZMAXFIOW ) will be the runtime then ( pm ) . - Fastest [ 0 ( nm ) MAXFIOW algorithm takes time . ] These algorithms complicated are . Can avoid using flaw algorithms ? ⑤ we

6 . Stoer-Wagner’s Algorithm ⑧ e ' eye i÷÷÷¥÷ - contraction Est } , " - lot 6/2*3 observation Key : the Cst ) Cr min is of either min cut The cut G) Est } minuet the or of -

7 Stoer-Wagner’s Algorithm # iterative The to observation leads an above ( proto ) algorithm : best so far cat found the 't be ( et C . while IGI 32 minimum which for in Find C is cat a a i . some Cst ) pain say , . w ( w CE ) 2 If c ) C . 't replace with C C . G ← GIES ,t3 3 Contract ( s 't ) and Let . .

8 find How such cat do ? we a Inca , ⑤ ( I a -4 A A- EV and For some Vote , - w ( aid ) E let w ( x , A) = , easy ) EE YEA n is most-Cited if se max { w ( n I 94A } , A ) , A) Cy = w .

g (G) MinCutPhase - vertex arbitrary is K A- ← { a } a an While AFV to most tightly connected A Let neha . If IAI IVI -2 = s ← se If IAI IVI I = - t ← a E ( A , a) Cc - set of A edges b/w and n A . A- ← Au la ] Contract Cst ) return

10 (G) MinCutPhase - vertex arbitrary is K A- ← { a } a an While AFV ( is to min most tightly connected A Let neha a . ( St ) - cut of the If IAI IVI -2 = last two - se vertices Sc addled If to A IAI IVI . l = - t c- a ( mtnyn ) E ( A , a) Ca - set of A o edges b/w and n A . A- ← A { a ] u Contract Cst ) return

11 ✓ 7 ' em .vn 8 v , 4 8 = biz weans , ⇒ its ::¥¥ ' = 20 Vg ) WCA , vz¥ I 6 v 9 9 Vz a= 1) A- { Yo } 2) w ( Erol , Va ) w ( { v , } , vi. 7=1 , Us ) w ( { Vol , = 8 and A { , ] = VG , Vg . w ( Evo , Vs } , Vt ) =L 3) 3 , # 1=-22 w ( Eva w( Eva , ↳ 3,41=5 , ↳ ,

"

" ÷ .

" i

" ÷ .

"

÷÷÷÷÷ '

13 Running Time - reduces by 1 size of G contraction the . each After during a cost incurred the Let 1- ( m ,n ) be (G) Mincutphase to call . ) OC Total time n .

14 Running Time - reduces by 1 size of G contraction the . each After during a cost incurred the Let 1- ( m ,n ) be (G) Mincutphase to call . T n' Yn ) 0 ( mn n ) ) . n -1cm , OC = Total time . - connected tightly vertex most next the Finding priority found be using queue can a . key ) ( Extract Increase Max , Timon ) ofmtnyn ) thus =

( * IS Proof of Correctness ( Each of the minimum cut phase is a - r graph current - t in cut the S , two the where and t are s last ) added vertices . induction by The proof is . arbitrary - cut C Cst ) Suppose is any . wCc* ) WCC ) show to E want we .

16 , Tc graph current so the Gr is - > induced partition C by . + a a • active ? is mis S T o . last is suppose vertex UV the added before ' added V was V - v ' and indifferent parts - is if u are V active in C .

17 set of added vertices before u the Av be Suppose . Sve Tvc =(AvVU2 ) Nc to = ( Ev3UA4nsc in - - - - . . . r . . , , → E- ( Ar , r ) U Tve sve T Sc - a Aru Ev } - = , - Tvc ) let = ( C Src : . , for show to vertex want we active u every , w ( Cr ) " ( v ) E Au , . -

' 8 set of added vertices before u the Av be Suppose . Sre Tvc = = Avnsc ¥:a ← Ann Tc . ÷ E- ( Arm ) E Cat I Sc Tvc ) let = ( Cr Src . , Ct C 't ( At and ) Note C = , 't ) w ( e ) W ( Edt ) c . = .

Inductive argument 19 - E- ( ¥ ) . § Base I case ! ° ! First vertex active - Av tV¥qv3 - . u w ( Cr ) Wl Av , u ) = . - -

Inductive argument 20 - § Base case ! ¥ First vertex active - Av tv¥qv3 - . ✓ Wl Av , wlcv ) u ) = . step : w ( Av , w ( cu ) Inductive v ) E suppose holds active vertex upto the v . first active vertex be me Let u after to added be V -

21 in LAu : ÷ . a . w ( Auu ) wCA w t = .

21 th • ÷ . ' Aun Sc T S C C w ( Au , u ) w ( Av , w ( Aal Av , n ) u ) t = . w C v ) u ) E Av ( Ar , But as u was s w connected vertex most tightly w.me Au the . chosen as .

21 th • ÷ . ' Aunsc T Sc c w ( Au ,u ) w ( Abu ) w ( Aal Av , n ) t = . m ) E w ( Ar w ( Aal Av , v ) t , . w ( Ar , r ) But W ( cu ) ( inductive E hypothesis )

" a. ÷¥÷÷:÷ . W ( Au , u ) w ( Av , w ( Aa u ) u ) l Av , t = . m ) E w ( Ar w CA n v ) t l Ar , , . on ) Ew E

21 u ) El Antar , U dy • y y a :c . ' Aun Sc T Sc c w ( Au , u ) w ( Abu ) w ( Aal Av , n ) t = . m ) E w ( Av , w ( Aal Av , v ) t . E ( Aa IA does not light edges u ) contribute blue in , only [ ✓ and to Cee .

21 , .u ) ELA f y ÷ : . an W ( Au , u ) w ( Av , w ( Au n ) u ) l Av , t = . m ) E u ( Ar , w CA n l Av , v ) t . E weed Ewes ) t w a (c) wA of * Is . - O .