Graph Coloring Independent Set and Coloring k -Coloring : 3-Coloring - PowerPoint PPT Presentation

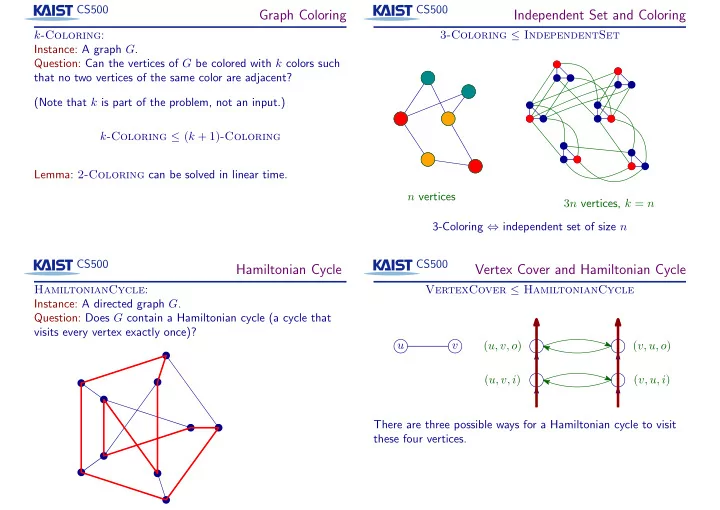
CS500 CS500 Graph Coloring Independent Set and Coloring k -Coloring : 3-Coloring ≤ IndependentSet Instance: A graph G . Question: Can the vertices of G be colored with k colors such that no two vertices of the same color are adjacent? (Note that k is part of the problem, not an input.) k -Coloring ≤ ( k + 1) -Coloring Lemma: 2-Coloring can be solved in linear time. n vertices 3 n vertices, k = n 3-Coloring ⇔ independent set of size n CS500 CS500 Hamiltonian Cycle Vertex Cover and Hamiltonian Cycle HamiltonianCycle : VertexCover ≤ HamiltonianCycle Instance: A directed graph G . Question: Does G contain a Hamiltonian cycle (a cycle that visits every vertex exactly once)? ( u, v, o ) ( v, u, o ) u v ( u, v, i ) ( v, u, i ) There are three possible ways for a Hamiltonian cycle to visit these four vertices.

CS500 CS500 Vertex Cover and Hamiltonian Cycle Vertex Cover and Hamiltonian Cycle VertexCover ≤ HamiltonianCycle VertexCover ≤ HamiltonianCycle u v ( u, v, o ) ( v, u, o ) u v ( u, v, o ) ( v, u, o ) ( u, v, i ) ( v, u, i ) ( u, v, i ) ( v, u, i ) There are three possible ways for a Hamiltonian cycle to visit There are three possible ways for a Hamiltonian cycle to visit these four vertices. these four vertices. CS500 CS500 Vertices of G Cover vertices k cover vertices connected to the ends of all vertex chains. v 1 ( u, v 1 , i ) v 2 u ( u, v 1 , i ) ( u, v 1 , o ) v 3 ( u, v 1 , o ) 1 v 4 ( u, v 2 , i ) ( u, v 2 , i ) 2 ( u, v 2 , o ) ( u, v 2 , o ) ( u, v 2 , o ) ( u, v 2 , o ) Vertex chain of u 3 ( u, v 3 , i ) ( u, v 3 , i ) ( u, v 3 , o ) ( u, v 3 , o ) k = 3 ( u, v 4 , i ) ( u, v 4 , i ) ( u, v 4 , o ) ( u, v 4 , o )

CS500 CS500 G has a vertex cover of size k if and only if G ′ has a G has a vertex cover of size k if and only if G ′ has a Hamiltonian path. Hamiltonian path. Let u 1 , u 2 , . . . , u k be the vertices of the vertex cover C . Then Let u 1 , u 2 , . . . , u k be the vertices of the vertex cover C . Then the Hamiltonian path starts in cover vertex 1 , visits the vertex the Hamiltonian path starts in cover vertex 1 , visits the vertex chain of u 1 , goes to cover vertex 2 , visits the vertex chain of chain of u 1 , goes to cover vertex 2 , visits the vertex chain of u 2 , and so on, until returning to cover vertex 1 . u 2 , and so on, until returning to cover vertex 1 . u v ( u, v, o ) ( v, u, o ) u v ( u, v, o ) ( v, u, o ) v �∈ C u ∈ C u ∈ C v ∈ C ( u, v, i ) ( v, u, i ) ( u, v, i ) ( v, u, i ) CS500 CS500 Example Example Cover u v u v u v u v w x w x w x w x

CS500 CS500 Subset Sum Summary SubsetSum : 3-Coloring ≤ IndependentSet Instance: A set X of positive integers and an integer t . 3-Coloring ≤ Planar3Coloring Question: Does X have a subset whose elements sum to t ? IndependentSet ≤ VertexCover VertexCover ≤ SubsetSum Number edges from 0 to m − 1 . IndependentSet ≤ Clique Our set X contains b i = 4 i for each edge i , and a v for each VertexCover ≤ SetCover vertex v : a v = 4 m + VertexCover ≤ HamiltonianCycle � 4 i . i ∈ ∆( v ) VertexCover ≤ SubsetSum The target sum t is SubsetSum ≤ Partition m − 1 HamiltonianCycle ≤ HamiltonianPath t = k · 4 m + � 2 · 4 i . HamiltonianPath ≤ LongestPath i =0