Generalizations of Gowers Theorem Dana Barto sov a (USP) - PowerPoint PPT Presentation

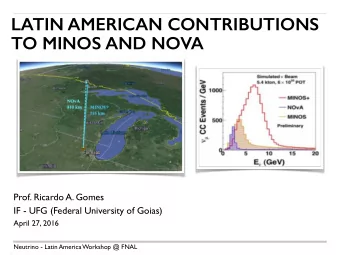
Generalizations of Gowers’ Theorem Dana Bartoˇ sov´ a (USP) Aleksandra Kwiatkowska (UCLA) BWB 2014 Maresias August 25-29, 2014 This work was supported by the grant FAPESP 2013/14458-9. Dana Bartoˇ sov´ a Generalizations of Gowers’ Theorem

Gowers’ c 0 Theorem Theorem (Gowers) Let ε > 0 and let F be any real-valued Lipschitz function on the unit sphere of c 0 . Then there is an infinite-dimensional subspace X on the unit sphere of which F varies by at most ε. Dana Bartoˇ sov´ a Generalizations of Gowers’ Theorem

Gowers’ c 0 Theorem Theorem (Gowers) Let ε > 0 and let F be any real-valued Lipschitz function on the unit sphere of c 0 . Then there is an infinite-dimensional subspace X on the unit sphere of which F varies by at most ε. Theorem (Gowers) Let ε > 0 and let F be any unconditional real-valued Lipschitz function on the unit sphere of c 0 . Then there is an infinite-dimensional positive block subspace X of c 0 on the unit sphere of which F varies by at most ε. Dana Bartoˇ sov´ a Generalizations of Gowers’ Theorem

Gowers’ c 0 Theorem Theorem (Gowers) Let ε > 0 and let F be any real-valued Lipschitz function on the unit sphere of c 0 . Then there is an infinite-dimensional subspace X on the unit sphere of which F varies by at most ε. Theorem (Gowers) Let ε > 0 and let F be any unconditional real-valued Lipschitz function on the unit sphere of c 0 . Then there is an infinite-dimensional positive block subspace X of c 0 on the unit sphere of which F varies by at most ε. P S ( c 0 ) - positive part of the sphere of c 0 Dana Bartoˇ sov´ a Generalizations of Gowers’ Theorem

Discretization � { 1 , (1 + ε ) − 1 , . . . , (1 + ε ) − ( k − 1) } , | supp( f ) | < ℵ 0 , { f : N ∃ n ∈ N f ( n ) = 1 } =: FIN k - (2 · ε )-net in P S ( c 0 ) (for sufficiently large k ) Dana Bartoˇ sov´ a Generalizations of Gowers’ Theorem

Discretization � { 1 , (1 + ε ) − 1 , . . . , (1 + ε ) − ( k − 1) } , | supp( f ) | < ℵ 0 , { f : N ∃ n ∈ N f ( n ) = 1 } =: FIN k - (2 · ε )-net in P S ( c 0 ) (for sufficiently large k ) F ( S ( c 0 )) ⊂ [ a, b ) = I 1 ∪ I 2 ∪ . . . ∪ I r - | I i | = | I j | ( a + rε ≥ b ) Dana Bartoˇ sov´ a Generalizations of Gowers’ Theorem

Discretization � { 1 , (1 + ε ) − 1 , . . . , (1 + ε ) − ( k − 1) } , | supp( f ) | < ℵ 0 , { f : N ∃ n ∈ N f ( n ) = 1 } =: FIN k - (2 · ε )-net in P S ( c 0 ) (for sufficiently large k ) F ( S ( c 0 )) ⊂ [ a, b ) = I 1 ∪ I 2 ∪ . . . ∪ I r - | I i | = | I j | ( a + rε ≥ b ) f ∈ FIN k � ( c ( f ) = i ← → F ( f ) ∈ I i ) Dana Bartoˇ sov´ a Generalizations of Gowers’ Theorem

FIN k � { 0 , 1 , 2 . . . , k } � supp( p ) = { n : p ( n ) � = 0 } p : N Dana Bartoˇ sov´ a Generalizations of Gowers’ Theorem

FIN k � { 0 , 1 , 2 . . . , k } � supp( p ) = { n : p ( n ) � = 0 } p : N � { 0 , 1 , . . . , k } : | supp( p ) | < ℵ 0 & ∃ n ( p ( n ) = k ) } FIN k = { p : N Dana Bartoˇ sov´ a Generalizations of Gowers’ Theorem

FIN k � { 0 , 1 , 2 . . . , k } � supp( p ) = { n : p ( n ) � = 0 } p : N � { 0 , 1 , . . . , k } : | supp( p ) | < ℵ 0 & ∃ n ( p ( n ) = k ) } FIN k = { p : N FIN 1 ↔ FIN( N ) Dana Bartoˇ sov´ a Generalizations of Gowers’ Theorem

FIN k � { 0 , 1 , 2 . . . , k } � supp( p ) = { n : p ( n ) � = 0 } p : N � { 0 , 1 , . . . , k } : | supp( p ) | < ℵ 0 & ∃ n ( p ( n ) = k ) } FIN k = { p : N FIN 1 ↔ FIN( N ) Tetris � FIN k − 1 T : FIN k Dana Bartoˇ sov´ a Generalizations of Gowers’ Theorem

FIN k � { 0 , 1 , 2 . . . , k } � supp( p ) = { n : p ( n ) � = 0 } p : N � { 0 , 1 , . . . , k } : | supp( p ) | < ℵ 0 & ∃ n ( p ( n ) = k ) } FIN k = { p : N FIN 1 ↔ FIN( N ) Tetris � FIN k − 1 T : FIN k T(p)(n)=max { 0,p(n)-1 } . Dana Bartoˇ sov´ a Generalizations of Gowers’ Theorem

FIN k � { 0 , 1 , 2 . . . , k } � supp( p ) = { n : p ( n ) � = 0 } p : N � { 0 , 1 , . . . , k } : | supp( p ) | < ℵ 0 & ∃ n ( p ( n ) = k ) } FIN k = { p : N FIN 1 ↔ FIN( N ) Tetris � FIN k − 1 T : FIN k T(p)(n)=max { 0,p(n)-1 } . Partial addition � p + q ( n ) = max { p ( n ) , q ( n ) } supp( p ) ∩ supp( q ) = ∅ Dana Bartoˇ sov´ a Generalizations of Gowers’ Theorem

Hindman’s Theorem FIN 1 ↔ FIN( N ) Dana Bartoˇ sov´ a Generalizations of Gowers’ Theorem

Hindman’s Theorem FIN 1 ↔ FIN( N ) � p + q = p ∪ q p ∩ q = ∅ Dana Bartoˇ sov´ a Generalizations of Gowers’ Theorem

Hindman’s Theorem FIN 1 ↔ FIN( N ) � p + q = p ∪ q p ∩ q = ∅ T ( p ) = ∅ Dana Bartoˇ sov´ a Generalizations of Gowers’ Theorem

Hindman’s Theorem FIN 1 ↔ FIN( N ) � p + q = p ∪ q p ∩ q = ∅ T ( p ) = ∅ Theorem (Hindman) � { 1 , 2 , . . . , r } be a finite colouring. Then there Let c : FIN( N ) is an infinite A ⊂ FIN( N ) such that FU(A) is monochromatic. Dana Bartoˇ sov´ a Generalizations of Gowers’ Theorem

Gowers’ for FIN k Block sequence B = ( b i ) ∞ i =1 ⊂ FIN k ( N ) s.t. max supp( b i ) < min supp( b i +1 ) Dana Bartoˇ sov´ a Generalizations of Gowers’ Theorem

Gowers’ for FIN k Block sequence B = ( b i ) ∞ i =1 ⊂ FIN k ( N ) s.t. max supp( b i ) < min supp( b i +1 ) � B � - partial subsemigroup generated by B, T, + , i.e. elements of the form Dana Bartoˇ sov´ a Generalizations of Gowers’ Theorem

Gowers’ for FIN k Block sequence B = ( b i ) ∞ i =1 ⊂ FIN k ( N ) s.t. max supp( b i ) < min supp( b i +1 ) � B � - partial subsemigroup generated by B, T, + , i.e. elements of the form l � T j s ( b s ) s =1 for some l ∈ N , b s ∈ B, j s ∈ { 0 , 1 , . . . , k } , and at least one j s = 0 . Dana Bartoˇ sov´ a Generalizations of Gowers’ Theorem

Gowers’ for FIN k Block sequence B = ( b i ) ∞ i =1 ⊂ FIN k ( N ) s.t. max supp( b i ) < min supp( b i +1 ) � B � - partial subsemigroup generated by B, T, + , i.e. elements of the form l � T j s ( b s ) s =1 for some l ∈ N , b s ∈ B, j s ∈ { 0 , 1 , . . . , k } , and at least one j s = 0 . Theorem (Gowers) � { 1 , 2 , . . . , r } be a finite colouring. Then there is Let c : FIN k an infinite block sequence B ⊂ FIN k such that � B � is monochromatic. Dana Bartoˇ sov´ a Generalizations of Gowers’ Theorem

Finite Gowers’ FIN k Theorem Theorem For every k, m, r, there exists n such that for every colouring � { 1 , 2 , . . . , r } there is a block sequence c : FIN k ( n ) B ⊂ FIN k ( n ) of length m such that � B � is monochromatic. Dana Bartoˇ sov´ a Generalizations of Gowers’ Theorem

Finite Gowers’ FIN k Theorem Theorem For every k, m, r, there exists n such that for every colouring � { 1 , 2 , . . . , r } there is a block sequence c : FIN k ( n ) B ⊂ FIN k ( n ) of length m such that � B � is monochromatic. g k ( m, r ) - smallest such n Dana Bartoˇ sov´ a Generalizations of Gowers’ Theorem

Finite Gowers’ FIN k Theorem Theorem For every k, m, r, there exists n such that for every colouring � { 1 , 2 , . . . , r } there is a block sequence c : FIN k ( n ) B ⊂ FIN k ( n ) of length m such that � B � is monochromatic. g k ( m, r ) - smallest such n Theorem (Tyros) g k ( m, r ) upper bounded by a primitive recursive function belonging to the class E 7 of Grzegorczyk’s hierarchy. Dana Bartoˇ sov´ a Generalizations of Gowers’ Theorem

Finite Gowers’ FIN k Theorem Theorem For every k, m, r, there exists n such that for every colouring � { 1 , 2 , . . . , r } there is a block sequence c : FIN k ( n ) B ⊂ FIN k ( n ) of length m such that � B � is monochromatic. g k ( m, r ) - smallest such n Theorem (Tyros) g k ( m, r ) upper bounded by a primitive recursive function belonging to the class E 7 of Grzegorczyk’s hierarchy. Theorem (Ojeda-Aristizabal) g k ( m, 2) ≤ f 4+2( k − 1) ◦ f 4 (6 m − 2) , where f i is the i -th function in the Ackermann Hierarchy. Dana Bartoˇ sov´ a Generalizations of Gowers’ Theorem

Type is a φ ∈ FIN k ( d ) such that φ ( i ) � = φ ( i + 1) . Dana Bartoˇ sov´ a Generalizations of Gowers’ Theorem

Type is a φ ∈ FIN k ( d ) such that φ ( i ) � = φ ( i + 1) . If A = ( a i ) d i =1 is a block sequence in FIN 1 ( n ) , then Dana Bartoˇ sov´ a Generalizations of Gowers’ Theorem

Type is a φ ∈ FIN k ( d ) such that φ ( i ) � = φ ( i + 1) . If A = ( a i ) d i =1 is a block sequence in FIN 1 ( n ) , then d � φ ( i ) · χ ( a i ) ∈ FIN k ( n ) i =1 Dana Bartoˇ sov´ a Generalizations of Gowers’ Theorem

Type is a φ ∈ FIN k ( d ) such that φ ( i ) � = φ ( i + 1) . If A = ( a i ) d i =1 is a block sequence in FIN 1 ( n ) , then d � φ ( i ) · χ ( a i ) ∈ FIN k ( n ) i =1 p ∈ FIN k ( n ) � ∃ φ ∈ FIN k ( d ) a type and ( a i ) d i =1 in FIN 1 ( n ) . Dana Bartoˇ sov´ a Generalizations of Gowers’ Theorem

Type is a φ ∈ FIN k ( d ) such that φ ( i ) � = φ ( i + 1) . If A = ( a i ) d i =1 is a block sequence in FIN 1 ( n ) , then d � φ ( i ) · χ ( a i ) ∈ FIN k ( n ) i =1 p ∈ FIN k ( n ) � ∃ φ ∈ FIN k ( d ) a type and ( a i ) d i =1 in FIN 1 ( n ) . d � p = φ ( i ) χ ( a i ) i =1 Dana Bartoˇ sov´ a Generalizations of Gowers’ Theorem