Funnel Heap - A Cache-Oblivious Priority Queue Gerth Stlting Brodal - PowerPoint PPT Presentation

Funnel Heap - A Cache-Oblivious Priority Queue Gerth Stølting Brodal Rolf Fagerberg BRICS University of Aarhus Thirteenth International Symposium on Algorithms and Computation Vancouver, BC, Canada, November 22, 2002 1

Outline of talk • Cache-oblivious model • Cache-oblivious results • Cache-oblivious priority queues • Funnel heap – k - merger – the data structure – operations Brodal, Fagerberg: Funnel Heap 2

The Classic RAM Model Add: O (1) R The RAM model: Mult: O (1) CPU A M Mem access: O (1) Brodal, Fagerberg: Funnel Heap 3

The Classic RAM Model Add: O (1) R The RAM model: Mult: O (1) CPU A M Mem access: O (1) L1 L2 R C C Real life: CPU a a A Disk c c M h h e e Bottleneck: transfer between two highest memory levels in use Brodal, Fagerberg: Funnel Heap 3

The I/O Model I/O M e m External CPU o r Memory y N = problem size M = memory size Aggarwal and Vitter 1988 B = I/O block size • One I/O moves B consecutive records from/to disk • Cost: number of I/Os � N N � Scan ( N ) = O ( N/B ) Sort ( N ) = O B log M/B B Brodal, Fagerberg: Funnel Heap 4

Cache-Oblivious Model Frigo, Leiserson, Prokop, Ramachandran 1999 • Program in the RAM model • Analyze in the I/O model (for arbitrary B and M ) Advantages • Optimal on arbitrary level ⇒ optimal on all levels • B and M not hard-wired into algorithm Brodal, Fagerberg: Funnel Heap 5

Cache-Oblivious Results • Scanning ⇒ stack, queue, selection, . . . • Sorting, matrix multiplication, FFT Frigo, Leiserson, Prokop, Ramachandran, FOCS’99 • Cache oblivious search trees Prokop 99 Bender, Demaine, Farach-Colton, FOCS’00 Rahman, Cole, Raman, WAE’01 Bender, Duan, Iacono, Wu and Brodal, Fagerberg, Jacob, SODA’02 • Priority queue and graph algorithms Arge, Bender, Demaine, Holland-Minkley, Munro, STOC’02 • Computational geometry Bender, Cole, Raman, ICALP’02 Brodal, Fagerberg, ICALP’02 • Scanning dynamic sets Bender, Cole, Demaine, Farach-Colton, ESA’02 Brodal, Fagerberg: Funnel Heap 6

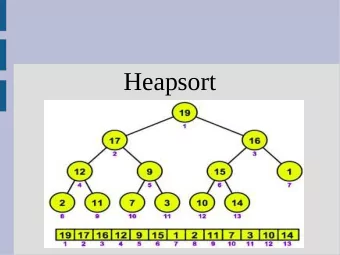
Priority Queues Insert ( e ) DeleteMin Classic RAM: • Heap: O (log 2 n ) time Williams 1964 Brodal, Fagerberg: Funnel Heap 7

Priority Queues Insert ( e ) DeleteMin Classic RAM: N � � • Heap: O (log 2 n ) time, O log 2 I/Os Williams 1964 M Brodal, Fagerberg: Funnel Heap 7

Priority Queues Insert ( e ) DeleteMin Classic RAM: N � � • Heap: O (log 2 n ) time, O log 2 I/Os Williams 1964 M I/O model: � 1 � Sort ( N ) � N � • Buffer tree: O B log M/B = O I/Os Arge 1995 B N Brodal, Fagerberg: Funnel Heap 7

Cache-Oblivious Priority Queues � 1 N � Arge, Bender, Demaine, • O B log M/B I/Os B Holland-Minkley, Munro 2002 – Uses sorting and selection as subroutines – Requires tall cache assumption, M ≥ B 2 Brodal, Fagerberg: Funnel Heap 8

Cache-Oblivious Priority Queues � 1 N � Arge, Bender, Demaine, • O B log M/B I/Os B Holland-Minkley, Munro 2002 – Uses sorting and selection as subroutines – Requires tall cache assumption, M ≥ B 2 • Funnel heap This talk – Uses only binary merging � 1 N i � – Profile adaptive, i.e. O B log M/B I/Os B N i is either the size profile, max depth profile, or #insertions during the lifetime of the i th inserted element Brodal, Fagerberg: Funnel Heap 8

Merge Trees s ✲ ✸ Binary merger Brodal, Fagerberg: Funnel Heap 9

Merge Trees s ✲ ✸ Binary merger q ✲ ✶ s ✲ q ✲ ✸ ✶ ❫ ✲ q ✲ ✶ ✣ s ✲ q ✲ ✸ ✶ ◆ ✲ q ✲ ✶ ✍ s ✲ q ✲ ✸ ✶ ❫ ✲ q ✲ ✶ ✣ s ✲ q ✲ ✸ ✶ Merge tree Brodal, Fagerberg: Funnel Heap 9

Merging Algorithm Fill ( v ) while out-buffer not full if left in-buffer empty Fill (left child) if right in-buffer empty q ✲ ✶ Fill (right child) s ✲ q ✲ ✸ ✶ perform one merge step ❫ ✲ q ✲ ✶ ✣ s ✲ q ✸ ✲ ✶ ◆ ✲ q ✲ ✶ ✍ s ✲ q ✸ ✲ ✶ ❫ ✲ q ✲ ✶ ✣ s ✲ q ✸ ✲ ✶ Brodal, Fagerberg: Funnel Heap 10

k - merger B 0 k 3 M 0 B 1 B √ · · · k → · · · M 1 M √ k M 0 B 1 M 1 B 2 M 2 B √ k M √ B 0 · · · k k Recursive memory layout Recursive defi nition of buffer sizes O ( k 3 B log M ( k 3 ) + k ) I/Os per invocation (if M ≥ B 2 ) Lemma: Frigo, Leiserson, Prokop, Ramachandran 1999 Brodal, Fagerberg 2002 Brodal, Fagerberg: Funnel Heap 11

The Priority Queue Link i v 1 v i A 1 A i ✛ ✛ ✛ ✛ · · · ✛ ✛ ✛ · · · ✛ ✛ ✻ ✻ ✻ ✻ B 1 B i ✻ ✻ ✻ ✻✻ I ✻ k i ✻✻ ✻ s 1 s 1 ✻✻ ✻ ·· · · · ✻✻ ✻ · · · · s i s i s i Brodal, Fagerberg: Funnel Heap 12

The Priority Queue Link i v 1 v i A 1 A i ✛ ✛ ✛ ✛ · · · ✛ ✛ ✛ · · · ✛ ✛ ✻ ✻ ✻ ✻ B 1 B i ✻ ✻ ✻ ✻✻ I ✻ k i ✻✻ ✻ s 1 s 1 ✻✻ ✻ ·· · · · ✻✻ ✻ · · · · s i s i s i k 4 / 3 k i +1 ≈ i s 4 / 3 s i +1 ≈ i s 1 / 3 k i ≈ i Brodal, Fagerberg: Funnel Heap 12

The Priority Queue Link i v 1 v i A 1 A i ✛ ✛ ✛ ✛ · · · ✛ ✛ ✛ · · · ✛ ✛ ✻ ✻ ✻ ✻ B 1 B i ✻ ✻ ✻ ✻✻ I ✻ k i ✻✻ ✻ s 1 s 1 ✻✻ ✻ ·· · · · ✻✻ ✻ · · · · s i s i s i k 4 / 3 k i +1 ≈ i s 4 / 3 s i +1 ≈ i s 1 / 3 k i In total: A single binary merge tree ≈ i Brodal, Fagerberg: Funnel Heap 12

Operations — DeleteMin A 1 v 1 · · · · · · I ·· · · · · · · · • If A 1 is empty, call Fill( v 1 ) • Search I and A 1 for minimum element Brodal, Fagerberg: Funnel Heap 13

Operations — Insert · · · · · · I k i c 1 ·· · · · c 2 · · · · c i • Insert in I • If I overflows, call Sweep( i ) for first i where c i ≤ k i Sweep ≈ addition of one to number c 1 c 2 ..c i ..c max s i = s 1 + � i − 1 j =1 k j s j Brodal, Fagerberg: Funnel Heap 14

Analysis · · · · · · ·· · · · · · · · We can prove: • Number N of insertions performed: s i max ≤ N � � 1 • Number of I/Os per Insert for link i : O B log M/B s i • By the doubly-exponentially growth of s i , the total number of I/Os per Insert is � 1 � ∞ � 1 � B log M/B N (3 / 4) k � O = O B log M/B N k =0 • DeleteMin is amortized for free Brodal, Fagerberg: Funnel Heap 15

Profile Adaptive · · · · · · ·· · · · · · · · • Modify Insert to apply Sweep ( i ) for – first i where c i ≤ k i , or – link i is at most half-full, i.e. there exists S ij 1 and S ij 2 that can be merged � 1 N i � • O B log M/B I/Os B Brodal, Fagerberg: Funnel Heap 16

Conclusions · · · · · · ·· · · · · · · · • Funnel heap - a cache-oblivious priority queue • Profile adaptive • Requires tall cache assumption (necessary requirement Brodal, Fagerberg 2002 ) Open problem • Worst-case bounds Brodal, Fagerberg: Funnel Heap 17