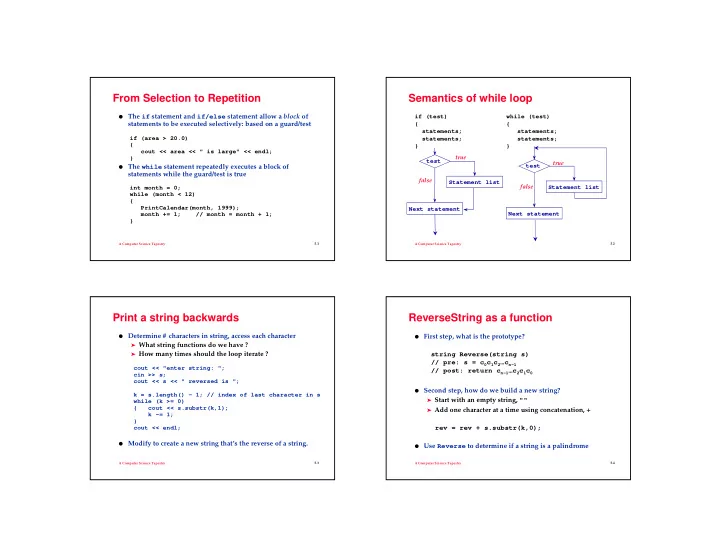

From Selection to Repetition Semantics of while loop ● The if statement and if/else statement allow a block of if (test) while (test) { { statements to be executed selectively: based on a guard/test statements; statements; if (area > 20.0) statements; statements; { } } cout << area << " is large" << endl; } true test true test ● The while statement repeatedly executes a block of statements while the guard/test is true false Statement list int month = 0; Statement list false while (month < 12) { PrintCalendar(month, 1999); Next statement month += 1; // month = month + 1; Next statement } A Computer Science Tapestry 5.1 A Computer Science Tapestry 5.2 Print a string backwards ReverseString as a function ● Determine # characters in string, access each character ● First step, what is the prototype? ➤ What string functions do we have ? string Reverse(string s) ➤ How many times should the loop iterate ? // pre: s = c 0 c 1 c 2 …c n-1 cout << "enter string: "; // post: return c n-1 …c 2 c 1 c 0 cin >> s; cout << s << " reversed is "; ● Second step, how do we build a new string? k = s.length() - 1; // index of last character in s ➤ Start with an empty string, "" while (k >= 0) { cout << s.substr(k,1); ➤ Add one character at a time using concatenation, + k -= 1; } cout << endl; rev = rev + s.substr(k,0); ● Modify to create a new string that’s the reverse of a string. ● Use Reverse to determine if a string is a palindrome A Computer Science Tapestry 5.3 A Computer Science Tapestry 5.4
Anatomy of a loop Infinite loops ● Initialize variables used in loop/loop test (before loop) ● Sometimes your program will be “stuck”, control-C to stop ➤ Loop test affected by initial values of variables ➤ What’s the problem in the loop below? Fixable? ● The loop test or guard is evaluated before each loop iteration cin >> num; ➤ NOT evaluated after each statement in loop int start = 0; ● The loop body must update some variable/expression used in while (start != 0) the loop test so that the loop eventually terminates { start += 2; ➤ If loop test is always true, loop is infinite cout << start << endl; } k = s.length() - 1; string rev = ""; while (k >= 0) ● It’s impossible to write one program that detects all infinite { rev = rev + s.substr(k,1); loops (the compiler doesn’t do the job, for example) k -= 1; } ➤ This can be proven mathematically, Halting Problem return rev; ➤ Some detection possible, but not universally A Computer Science Tapestry 5.5 A Computer Science Tapestry 5.6 Developing Loops Factorial ● N! = 1x2x…xN is “N factorial”, used in math, statistics ● Some loops are easy to develop code for, others are not ➤ Sometimes the proper loop test/body are hard to design int factorial(int n) ➤ Techniques from formal reasoning/logic can help // pre: 0 <= n // post: returns n! (1 x 2 x … x n) ● Practice helps, but remember ➤ Good design comes from experience, experience comes ● We’ll return the value of a variable product , we’ll need to from bad design accumulate the answer in product ● There are other looping statements in addition to while , but ➤ The loop will iterate n times, mutiplying by 1, 2, …, n they don’t offer anything more powerful, just some syntactic ➤ Alternatives: how many multiplications are needed? convenience ➤ If product holds the answer, then product == n! when ➤ for loop the loop terminates ➤ do-while loop • Use this to help develop the loop A Computer Science Tapestry 5.7 A Computer Science Tapestry 5.8
Factorial continued Long, int, and BigInt ● If product holds the answer, then product == n! when the ● On some systems the type long int ( long ) provides a loop terminates, replace n with count , the looping variable greater range than int ➤ Invariant: product == count! ➤ With 32-bit (modern) compilers/operating systems int is roughly –2 billion to 2 billion, but on 16-bit machines the long Factorial(int num) range is usually –32,768 to 32,767 [how many values?] // precondition: num >= 0 // postcondition returns num! ➤ 13! Is 1,932,053,504, so what happens with 14! { long product = 1; int count = 0; ● The type BigInt , accessible via #include " bigint.h " can while (count < num) be used like an int , but gets as big as you want it to be { count += 1; ➤ Really arbitrarily large? product *= count; ➤ Disadvantages of using BigInt compared to int ? } return product; } A Computer Science Tapestry 5.9 A Computer Science Tapestry 5.10 Determining if a number is prime Determining Primality (continued) ● Cryptographic protocols depend on prime numbers ● 2 is prime, 3 is prime, 5 is prime, 17 is prime, … 137, 193? ➤ Determining if a number is prime must be “easy” ➤ To check 137, divide it by 3, 5, 7, 9, 11, 13 ➤ Actually factoring a number must be “hard” ➤ To check 193, divide it by 3 ,5, 7, 9, 11, 13 ➤ What does hard mean? What factors affect difficulty? • Note that 14x14 = 196, why is 13 largest potential factor? • How do we determine if a number is divisible by another? ● PGP (pretty good privacy) and e-commerce depend on secure/encrypted transactions ● We’ll check odd numbers as potential divisors ➤ What are government restrictions on exporting PGP? ➤ Treat even numbers as special case, avoid lengthy testing ➤ Different versions of Netscape in US and other countries? ➤ Watch out for 2, special case of even number ➤ Instead of odd numbers, what would be better as tests? ● Sophisticated mathematics used for easy prime-testing, we’ll ➤ How many times will our testing loop iterate to determine do basic prime testing that’s reasonably fast, but not good if n is prime? enough for encryption (why not?) ➤ See primes.cpp for code A Computer Science Tapestry 5.11 A Computer Science Tapestry 5.12
Details of IsPrime in primes.cpp C++ details: syntax and shorthand ● Several different return statements are written, only one is ● With while loops and variables we can write a program to do executed when function executes anything a program can be written for ➤ The return statement immediately tops, return to call ➤ Other language features make programs easier to develop and maintain: functions, if statements, other statements ➤ Some people think functions should have one return ➤ Yet, we want to avoid needing to understand many, many • Potentially easier to debug and reason about, language features if we don’t have to • Often introduces extraneous variables/tests ➤ You’ll read code written by others who may use features ● To assign a double value to an int , a typecast is used, tell the compiler that the loss of precision is ok ● Loops are statements, can be combined with other loops, with if statements, in functions, etc. ➤ Fix all compiler warnings whenever possible ● Other kinds of looping statements can make programming ➤ Make casts explicit, tell the compiler you know what you simpler to develop and maintain are doing ● Similar shorthand for other language features: x = x + 1; ● What about complexity/efficiency of IsPrime ? A Computer Science Tapestry 5.13 A Computer Science Tapestry 5.14 The for loop Example: add up digits of a number ● In many coding problems a definite loop is needed ● If we have a number like 27 or 1,618 what expression yields the number of digits in the number (hint, think log) ➤ Number of iterations known before loop begins and simple to calculate and use in loop (counting loop) • Example: length of string: print a string vertically ➤ Which digit is easiest to get, how can we access it? ➤ How can we chop off one digit at-a-time? void Vertical(string s) // post: chars of s printed vertically int digitSum(int n) // post: returns sum of digits in n int len = s.length(); // for loop alternative { int k = 0; for(k=0; k < len; k+= 1) // what’s needed here? while (k < len) { cout << s.substr(k,0); while (n > 0) // for loop alternative? { cout << s.substr(k,0); } { sum += n % 10; k += 1; // what’s needed here? } } ● Initialization, test, update are localized into one place, harder return sum; to leave update out, for example } A Computer Science Tapestry 5.15 A Computer Science Tapestry 5.16
Recommend
More recommend