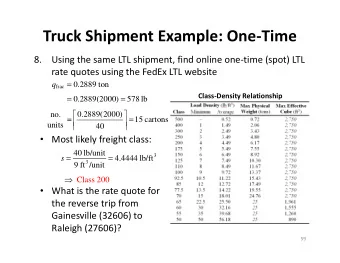
From LTL to Deterministic Parity Automata Javier Esparza 1 Jan K - PowerPoint PPT Presentation

From LTL to Deterministic Parity Automata Javier Esparza 1 Jan K ř etínsk ý 1 Salomon Sickert 1 Jean-François Raskin 2 1. Technische Universität München 2. Université libre de Bruxelles 1

R EACTIVE S YNTHESIS Specification Controller LTL 2

R EACTIVE S YNTHESIS Specification Controller Nondeterministic Büchi LTL NBA 2

R EACTIVE S YNTHESIS Specification Controller Nondeterministic Büchi LTL NBA DPA Deterministic Parity 2

R EACTIVE S YNTHESIS Specification Controller Nondeterministic Büchi LTL NBA DPA Parity Game Deterministic Parity 2

R EACTIVE S YNTHESIS Specification Controller Nondeterministic Büchi LTL NBA DPA Parity Game Controller Deterministic Parity 2

R EACTIVE S YNTHESIS Specification Controller LTL NBA DPA Parity Game Controller • SYNTCOMP 2016 / LTL Synthesis Track • Tools: Acacia(4Aiger), BoSy, PARTY, Unbeast • Techniques: Bounded Synthesis, Antichains, BDDs • No tool relied on parity games! 2

R EACTIVE S YNTHESIS Specification Controller LDBA LTL NBA DPA Parity Game Controller • SYNTCOMP 2016 / LTL Synthesis Track Goal: • Tools: Acacia(4Aiger), BoSy, PARTY, Unbeast • Techniques: Bounded Synthesis, Antichains, BDDs Find a translation to make synthesis using Parity games competitive! • No tool relied on parity games! 2

L IMIT -D ETERMINISTIC B ÜCHI A UTOMATA Initial Component Accepting Component “ Jumps” deterministic non-deterministic Also known as: deterministic-in-the-limit or semi-deterministic 3

L IMIT -D ETERMINISTIC B ÜCHI A UTOMATA Initial Component Accepting Component “ Jumps” deterministic non-deterministic Also known as: deterministic-in-the-limit or semi-deterministic 3

L IMIT -D ETERMINISTIC B ÜCHI A UTOMATA Initial Component Accepting Component “ Jumps” deterministic non-deterministic Also known as: deterministic-in-the-limit or semi-deterministic 3

Simple, optimal and practical translation from LTL to DPA (via LDBA) 4

without Safra-trees (or similar approaches) Simple, optimal and practical translation from LTL to DPA (via LDBA) 4

without Safra-trees (or similar approaches) 2-Exp Simple, optimal and practical translation from LTL to DPA (via LDBA) 4

without Safra-trees (or similar approaches) 2-Exp yields small automata in practice Simple, optimal and practical translation from LTL to DPA (via LDBA) 4

LDBA R UN DAG No branching on the right side! × × Initial Component Accepting Component (non-deterministic) (deterministic) 5

LDBA R UN DAG Position: 3 2 1 6

LDBA R UN DAG Position: 3 2 1 6

LDBA R UN DAG • Facts: • No branching • All infinite branches eventually stabilise at a specific position. Position: 3 2 1 6

LDBA R UN DAG • Facts: • No branching • All infinite branches eventually stabilise at a specific position. • Idea: • Parity condition identifies the oldest accepting run. Position: 3 2 1 6

LDBA R UN DAG • Facts: • No branching • All infinite branches eventually stabilise at a specific position. • Idea: • Parity condition identifies the oldest accepting run. Position: 3 2 1 6

LDBA R UN DAG • Facts: • No branching • All infinite branches eventually stabilise at a specific position. • Idea: • Parity condition identifies the oldest accepting run. Position: 3 2 1 6

LDBA R UN DAG • Facts: • No branching • All infinite branches eventually stabilise at a specific position. • Idea: • Parity condition identifies the oldest accepting run. Position: 3 2 1 6

LDBA R UN DAG • Facts: • No branching • All infinite branches eventually stabilise at a specific position. • Idea: • Parity condition identifies the oldest accepting run. Position: 3 2 1 6

LDBA R UN DAG • Facts: • No branching • All infinite branches eventually stabilise at a specific position. • Idea: • Parity condition identifies the oldest accepting run. Position: 3 2 1 6

LTL → DPA • Facts: • LTL → LDBA is exactly 2-Exp [S, Esparza, Jaax, Kretínsk ý CAV’16] • LDBA → DPA is exactly Exp • Naive combination of with LDBA → DPA yields a 3-Exp construction. • However, the translation LTL → DPA should be 2-Exp! 7

P RUNED R UN DAG L 3 L 2 L 1 × × Initial Component Accepting Component (non-deterministic) (deterministic) 8

P RUNED R UN DAG Oracle: L 2 ⊆ L 1 L 3 L 2 L 1 × × Initial Component Accepting Component (non-deterministic) (deterministic) 8

P RUNED R UN DAG Oracle: L 2 ⊆ L 1 L 3 L 2 L 1 × × × × × Initial Component Accepting Component (non-deterministic) (deterministic) 8

P RUNED R UN DAG Oracle: L 3 ⊆ L 2 ∪ L 1 L 3 L 2 L 1 × × Initial Component Accepting Component (non-deterministic) (deterministic) 8

P RUNED R UN DAG Oracle: L 3 ⊆ L 2 ∪ L 1 L 3 L 2 L 1 × × × × × Initial Component Accepting Component (non-deterministic) (deterministic) 8

CONCLUSION • Presented Construction: • Simpler Structure: rankings (lists) vs. Safra-trees • Optimal for LDBA → DPA and LTL → DPA (with pruning) • On-the-fly construction • Future Work: • Design a NBA → LDBA translation, which can be easily pruned. • Provide a complete synthesis toolchain combined with a parity game solver. • Publication: • From LTL and Limit-Deterministic Büchi Automata to Deterministic Parity Automata. TACAS’17 • Website: https://www7.in.tum.de/~sickert/projects/ltl2dpa 9

L ANDSCAPE OF A UTOMATA DRA LTL NBA DPA LDBA DMA N ondeterministic L imit- D eterministic D eterministic EXP 2-EXP 3-EXP Acceptance Conditions: B üchi R abin P arity M uller 10

L ANDSCAPE OF A UTOMATA DRA Tableaux, Alternating Automata LTL NBA DPA LDBA DMA N ondeterministic L imit- D eterministic D eterministic EXP 2-EXP 3-EXP Acceptance Conditions: B üchi R abin P arity M uller 10

L ANDSCAPE OF A UTOMATA DRA Safra-Piterman trees, Skeleton trees Tableaux, Alternating Automata LTL NBA DPA LDBA DMA N ondeterministic L imit- D eterministic D eterministic EXP 2-EXP 3-EXP Acceptance Conditions: B üchi R abin P arity M uller 10

L ANDSCAPE OF A UTOMATA DRA Safra-Piterman trees, Skeleton trees Tableaux, Alternating Automata LTL NBA DPA Breakpoints LDBA DMA N ondeterministic L imit- D eterministic D eterministic EXP 2-EXP 3-EXP Acceptance Conditions: B üchi R abin P arity M uller 10

L ANDSCAPE OF A UTOMATA Focus on F and G , Rabinizer DRA Safra-Piterman trees, Skeleton trees Tableaux, Alternating Automata LTL NBA DPA Breakpoints LDBA DMA N ondeterministic L imit- D eterministic D eterministic EXP 2-EXP 3-EXP Acceptance Conditions: B üchi R abin P arity M uller 10

L ANDSCAPE OF A UTOMATA Focus on F and G , Rabinizer DRA Safra-Piterman trees, Skeleton trees Tableaux, Alternating Automata LTL NBA DPA Breakpoints LDBA DMA Focus on F and G , Kini, [CAV’16] N ondeterministic L imit- D eterministic D eterministic EXP 2-EXP 3-EXP Acceptance Conditions: B üchi R abin P arity M uller 10

L ANDSCAPE OF A UTOMATA Focus on F and G , Rabinizer DRA Safra-Piterman trees, Appearance Records Skeleton trees Tableaux, Alternating Automata LTL NBA DPA Breakpoints LDBA DMA Focus on F and G , Kini, [CAV’16] N ondeterministic L imit- D eterministic D eterministic EXP 2-EXP 3-EXP Acceptance Conditions: B üchi R abin P arity M uller 10

L ANDSCAPE OF A UTOMATA Focus on F and G , Rabinizer DRA Safra-Piterman trees, Appearance Records Skeleton trees Tableaux, Alternating Automata LTL NBA DPA Breakpoints LDBA DMA Focus on F and G , Kini, [CAV’16] N ondeterministic L imit- D eterministic D eterministic EXP 2-EXP 3-EXP Acceptance Conditions: B üchi R abin P arity M uller 10

L ANDSCAPE OF A UTOMATA Focus on F and G , Rabinizer DRA Safra-Piterman trees, Appearance Records Skeleton trees Tableaux, Alternating Automata LTL NBA DPA Breakpoints LDBA DMA Focus on F and G , Kini, [CAV’16] N ondeterministic L imit- D eterministic D eterministic EXP 2-EXP 3-EXP Acceptance Conditions: B üchi R abin P arity M uller 10

L ANDSCAPE OF A UTOMATA DRA LTL NBA DPA LDBA DMA N ondeterministic L imit- D eterministic D eterministic EXP 2-EXP 3-EXP Acceptance Conditions: B üchi R abin P arity M uller 11

L ANDSCAPE OF A UTOMATA DRA LTL NBA DPA LDBA DMA N ondeterministic L imit- D eterministic D eterministic Acceptance Conditions: B üchi R abin P arity M uller 12

L ANDSCAPE OF A UTOMATA DRA Probabilistic MC LTL NBA DPA LDBA DMA N ondeterministic L imit- D eterministic D eterministic Acceptance Conditions: B üchi R abin P arity M uller 12

L ANDSCAPE OF A UTOMATA DRA Probabilistic MC LTL NBA DPA Synthesis via Parity Games: • positional strategies • efficient solvers available LDBA DMA N ondeterministic L imit- D eterministic D eterministic Acceptance Conditions: B üchi R abin P arity M uller 12