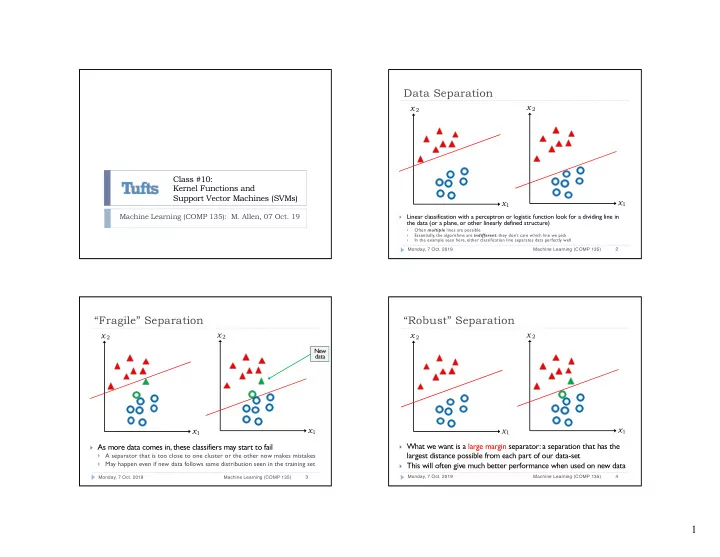

Data Separation x 2 x 2 Class #10: Kernel Functions and Support Vector Machines (SVMs) x 1 x 1 Machine Learning (COMP 135): M. Allen, 07 Oct. 19 Linear classification with a perceptron or logistic function look for a dividing line in } the data (or a plane, or other linearly defined structure) Often multiple lines are possible } Essentially, the algorithms are indifferent : they don’t care which line we pick } In the example seen here, either classification line separates data perfectly well } 2 Monday, 7 Oct. 2019 Machine Learning (COMP 135) “Fragile” Separation “Robust” Separation x 2 x 2 x 2 x 2 New data x 1 x 1 x 1 x 1 } What we want is a large margin separator: a separation that has the } As more data comes in, these classifiers may start to fail largest distance possible from each part of our data-set } A separator that is too close to one cluster or the other now makes mistakes } May happen even if new data follows same distribution seen in the training set } This will often give much better performance when used on new data 4 Monday, 7 Oct. 2019 Machine Learning (COMP 135) 3 Monday, 7 Oct. 2019 Machine Learning (COMP 135) 1
Large Margin Separation Linear Classifiers and SVMs x 2 Linear This is sometimes called the Weight equation w · x = w 0 + w 1 x 1 + w 2 x 2 + · · · + w n x n “widest road” approach ( 1 w · x ≥ 0 Threshold function h w = A support vector machine (SVM) 0 w · x < 0 is a technique that finds this road. The points that define the edges SVM of the road are the support vectors. x 1 Weight equation w · x + b = ( w 1 x 1 + w 2 x 2 + · · · + w n x n ) + b } A new learning problem: find the separator with the largest margin ( +1 w · x ≥ 0 } This will be measured from the data points, on opposite sides, that Threshold function h w = w · x < 0 − 1 are closest together 6 Monday, 7 Oct. 2019 Machine Learning (COMP 135) 5 Monday, 7 Oct. 2019 Machine Learning (COMP 135) Large Margin Separation Mathematics of SVMs x 2 x 2 w · x + + b = +1 w · x − + b = − 1 w · x + b = 0 +1 x + w · ( x + − x − ) = 2 A key difference: the SVM is going –1 2 to do this without learning and w || w || · ( x + − x − ) = remembering weight vector w . || w || x – Instead, it will use features of the data-items themselves . q || w || = w 2 1 + w 2 2 + · · · + w 2 x 1 x 1 n } Like a linear classifier, the SVM separates at the line where its learned } It turns out that the weight-vector w for the largest margin separator vector of weights is zero has some important properties relative to the closest data-points on each side ( x + and x – ) 8 Monday, 7 Oct. 2019 Machine Learning (COMP 135) 7 Monday, 7 Oct. 2019 Machine Learning (COMP 135) 2
Mathematics of SVMs Mathematics of SVMs } The details of how all this is done are a bit complicated, but a } Through the magic of mathematics (Lagrangian multipliers, to constrained optimization problem like this can be algorithmically be specific), we can derive a quadratic programming problem solved to get all of the 𝛽 i values needed: We start with our data-set: 1. α i − 1 X X W ( α ) = α i α j y i y j ( x i · x j ) { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x n , y n ) } [ ∀ i, y i ∈ { +1 , − 1 } ] 2 i i,j We then solve the constrained optimization problem: 2. ∀ i, α i ≥ 0 α i − 1 X X W ( α ) = α i α j y i y j ( x i · x j ) X α i y i = 0 2 i i,j i The goal : based on known values ( ) x i , y i ∀ i, α i ≥ 0 } Once done, we can find the weight-vector and bias term if we want: find the values we don’t know ( 𝛽 i ) that: X 1. Will maximize value W ( 𝛽 i ) α i y i = 0 b = − 1 X w = 2( max i | y i = − 1 w · x i + j | y j =+1 w · x j ) min α i y i x i 2. Satisfy the two numerical constraints i i 10 Monday, 7 Oct. 2019 Machine Learning (COMP 135) 9 Monday, 7 Oct. 2019 Machine Learning (COMP 135) The Dual Formulation Sparseness of SVMs x 2 } It turns out that we don’t need to use the weights at all This means that when we do the } Instead, we can simply use the 𝛽 i values directly : classification calculation: 𝛽 i = 0 X α j y j ( x i · x j ) − b X w · x i + b = α j y j ( x i · x j ) − b j We only have to sum over points 𝛽 + j x j that are in the set of support vectors, ignoring all others. } Now, if we had to sum over every data-point like we do 𝛽 – Thus, an SVM need only on the right-hand side of this equation, this would look remember and use the values for very bad for a large data-set the few support vectors, not } It turns out that these 𝛽 i values have a special property, x 1 those for all the rest of the data. however, that makes it feasible to use them as part of our } The 𝛽 i values are 0 everywhere except at the support vectors classification function… (the points closest to the separator) 12 Monday, 7 Oct. 2019 Machine Learning (COMP 135) 11 Monday, 7 Oct. 2019 Machine Learning (COMP 135) 3
Another Nice Trick Transforming Non-Separable Data x 2 x 2 X α j y j ( x i · x j ) − b j A transformation function: Using a kernel “trick”, we can find ϕ : R n → R m ϕ ( x ) a function that transforms the maps data-vectors to new data into another form, where it vectors, of either the same is actually possible to separate it dimensionality ( m = n ) or a in a linear manner. different one ( m ≠ n ) x 1 x 1 } If data that is not linearly separable, we can transform it } The calculation uses dot-products of data-points with each } We change features used to represent our data other (instead of with weights) } Really, we don’t care what the data feature are, so long as we can get } This will allow us to deal with data that is not linearly separable classification to work 14 Monday, 7 Oct. 2019 Machine Learning (COMP 135) 13 Monday, 7 Oct. 2019 Machine Learning (COMP 135) Image source: Russel & Norvig, AI: A Transforming Non-Separable Data The “Kernel Trick” Modern Approach (Prentice Hal, 2010) x 2 x 2 ϕ ( ) 1.5 ϕ ( ) ϕ ( ) 1 √ 2 x 1 x 2 ϕ ( ) ϕ ( ) 3 0.5 2 ϕ ( ) 1 x 2 0 ϕ ( ) 0 -1 ϕ ( ) 2.5 ϕ ( ) -0.5 -2 2 -3 ϕ ( ) 0 1.5 -1 0.5 2 1 x 2 1 1.5 2 0.5 x 1 -1.5 2 x 1 x 1 -1.5 -1 -0.5 0 0.5 1 1.5 x 1 X α j y j ( ϕ ( x i ) · ϕ ( x j )) − b (a) (b) ϕ : R n → R m ϕ ( x ) j √ ϕ ( x 1 , x 2 ) = ( x 2 1 , x 2 2 x 1 x 2 ) 2 , 16 Monday, 7 Oct. 2019 Machine Learning (COMP 135) 15 Monday, 7 Oct. 2019 Machine Learning (COMP 135) 4
The Kernel Function Simplifying the Transformation Function } We can derive a simpler (2-dimensional) equation, equivalent to the cross-product needed when doing SVM computations k ( x , z ) = ϕ ( x ) · ϕ ( z ) = ( x · z ) 2 in the transformed (3-dimensional) space: ϕ ( x ) · ϕ ( z ) = ( x 2 1 , x 2 √ 2 x 1 x 2 ) · ( z 2 1 , z 2 √ 2 z 1 z 2 ) Needed 2 , 2 , } This final function (right side) is what the SVM will = x 2 1 z 2 1 + x 2 2 z 2 √ √ actually use to compute dot-products in its equations 2 + 2 x 1 x 2 2 z 1 z 2 10 multiplications } This is called the kernel function = x 2 1 z 2 1 + x 2 2 z 2 2 + 2 x 1 x 2 z 1 z 2 2 additions = ( x 1 z 1 + x 2 z 2 ) 2 } To make SVMs really useful we look for a kernel that: 3 multiplications = ( x · z ) 2 1 addition Separates the data usefully 1. Is relatively efficient to calculate 2. Used instead 18 Monday, 7 Oct. 2019 Machine Learning (COMP 135) 17 Monday, 7 Oct. 2019 Machine Learning (COMP 135) This Week } T oday : Kernels and SVMs } Readings : Linked from class website schedule page. } Homework 03 : due Wednesday, 16 October, 9:00 AM } Office Hours : 237 Halligan, Tuesday, 11:00 AM – 1:00 PM } TA hours can be found on class website as well Monday, 7 Oct. 2019 Machine Learning (COMP 135) 19 5
Recommend
More recommend