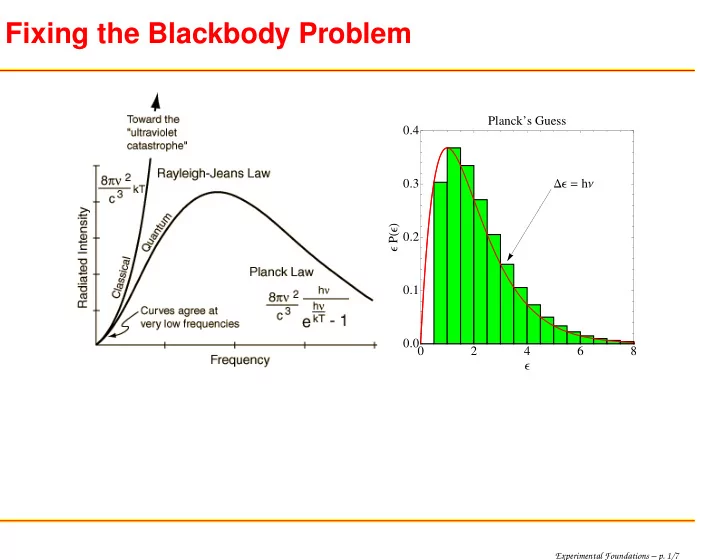
Fixing the Blackbody Problem Plancks Guess 0.4 0.3 h P 0.2 - PowerPoint PPT Presentation

Fixing the Blackbody Problem Planck’s Guess 0.4 0.3 �Ε � h Ν Ε P � Ε � 0.2 0.1 0.0 0 2 4 6 8 Ε Experimental Foundations – p. 1/7

Electromagnetic Waves See more and here and here. Experimental Foundations – p. 2/7

Double-Slit Interference d Interfering waves Experimental Foundations – p. 3/7

Diffraction Electron diffraction by gold X-ray diffraction by Cr 2 O 3 Experimental Foundations – p. 4/7

Matter Waves Experimental Foundations – p. 5/7

Electromagnetic Waves See more here and here. Experimental Foundations – p. 6/7

The Postulates 1. Each physical, measurable quantity, A , has a corresponding operator, A , that satisfies the eigenvalue equation ˆ ˆ A φ = aφ and measuring that quantity yields the eigenvalues of ˆ A .

The Postulates 1. Each physical, measurable quantity, A , has a corresponding operator, A , that satisfies the eigenvalue equation ˆ ˆ A φ = aφ and measuring that quantity yields the eigenvalues of ˆ A . 2. Measurement of the observable A leaves the system in a state that is an eigenfunction of ˆ A .

The Postulates 1. Each physical, measurable quantity, A , has a corresponding operator, A , that satisfies the eigenvalue equation ˆ ˆ A φ = aφ and measuring that quantity yields the eigenvalues of ˆ A . 2. Measurement of the observable A leaves the system in a state that is an eigenfunction of ˆ A . 3. The state of a system is represented by a wave function Ψ which is continuous, differentiable and contains all the information about it. The average value of any observable A is determined by all space Ψ ∗ ˆ � � A � = A Ψ d� r . The ‘intensity’ is proportional to | Ψ | 2 .

The Postulates 1. Each physical, measurable quantity, A , has a corresponding operator, A , that satisfies the eigenvalue equation ˆ ˆ A φ = aφ and measuring that quantity yields the eigenvalues of ˆ A . 2. Measurement of the observable A leaves the system in a state that is an eigenfunction of ˆ A . 3. The state of a system is represented by a wave function Ψ which is continuous, differentiable and contains all the information about it. The average value of any observable A is determined by all space Ψ ∗ ˆ � � A � = A Ψ d� r . The ‘intensity’ is proportional to | Ψ | 2 . 4. The time development of the wave function is determined by = − � 2 i � ∂ Ψ( � r, t ) 2 µ ∇ 2 Ψ( � r, t ) + V ( � r )Ψ( � r, t ) µ ≡ reduced mass. ∂t Experimental Foundations – p. 7/7